Слайд 2
Слово "логика" греческого происхождения. Логика как наука
основана Аристотелем (384-320
гг до н.э.), который был
необыкновенной фигурой в целой
плеяде блестящих греческих
ученых. Он был последователем Платона и посещал его Академию в
Афинах. После смерти Платона (347 г.до н.э.) Аристотель покинул
Афины. Он вернулся туда 12 лет спустя и основал свою школу –
Лицей. Одним из учеников Аристотеля был Александр Великий.
Слайд 3
Логические задачи
Решать логические задачи очень увлекательно.
Известно несколько
различных способов решения логических задач. Давайте назовем их так:
Метод
рассуждений;
Метод таблиц;
Метод графов;
Метод блок-схем;
Метод бильярда;
Метод кругов Эйлера.
Способ рассуждений - самый легкий способ.
Этим способом решаются самые простые логические задачи
Слайд 4
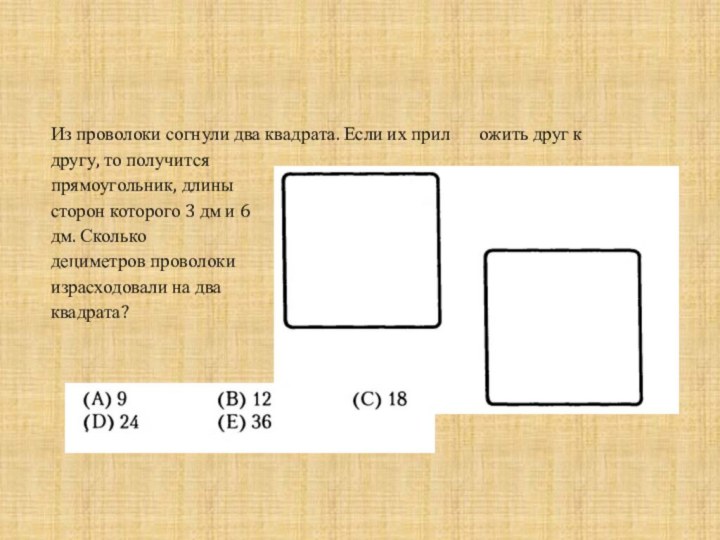
Решим старинную китайскую задачу.
В клетке находятся
фазаны и кролики. Известно, что у них 35 голов
и 94 ноги. Узнайте число фазанов и число кроликов.
Фазаны и кролики
Слайд 5
Решение: Представим, что на верх клетки, в которой
сидят фазаны и кролики, положили морковку. Все кролики встанут
на задние лапы, чтобы дотянуться до морковки. Сколько ног в этот момент будет стоять на земле? 35 * 2 = 70
Но в условии даны 94 ноги, где же остальные? Остальные не посчитаны – это передние лапы кроликов. Сколько их? 94 -70 = 24 (лапы). Сколько же кроликов? 24 : 2 = 12 (кроликов). А фазанов? 35 – 12 = 23 фазана.
Ответ: 23 фазана и 12 кроликов
Слайд 6
Жуки и пауки
У меня в одной коробке есть
жуки
И еще в другой коробке - пауки.
Мало их, в
дну минуту можно счесть;
Пауков с жуками вместе - только шесть.
Стал считать я в двух коробках сколько ног
Очень долго сосчитать я их не мог.
Оказалось ног немало - сорок две,
Ну, скажи теперь мне сколько тут жуков?
И еще сочти отдельно пауков.
Слайд 7
Гуси и крольчата
В теплом хлеве у бабуси
Жили
кролики и гуси.
Бабка странная была
Счет животных так
вела
Выйдет утром за порог,
Сосчитает 300 ног,
А потом без лишних слов
Насчитает 100 голов
И с спокойною душой
Идет снова на покой
Кто ответит поскорей
Сколько было там гусей?
Кто узнает из ребят
Сколько было там крольчат?
Слайд 8
Математика полезна тем, что она трудна.
Окружающий наш мир
- это мир геометрии
А.Д.Александров
Слайд 9
А
D
Б
В
Г
К
М
Ш
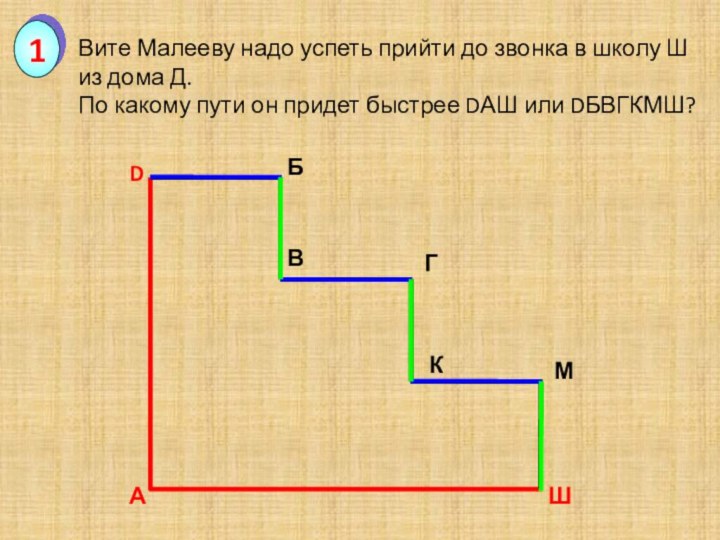
Вите Малееву надо успеть прийти до звонка в
школу Ш из дома Д.
По какому пути он
придет быстрее DАШ или DБВГКМШ?
1
Слайд 10
В открытую прямоугольную бочку налита вода, на первый
взгляд, до половины. Как убедиться, что это не так?
4
Слайд 11
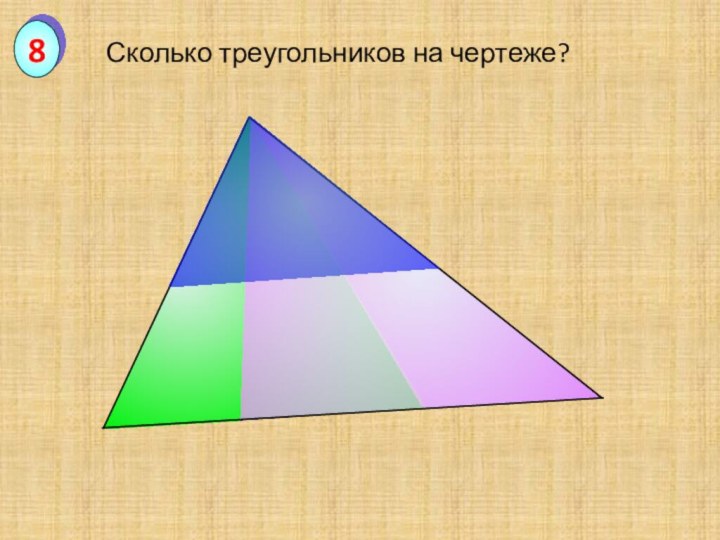
Сколько треугольников на чертеже?
8
Слайд 12
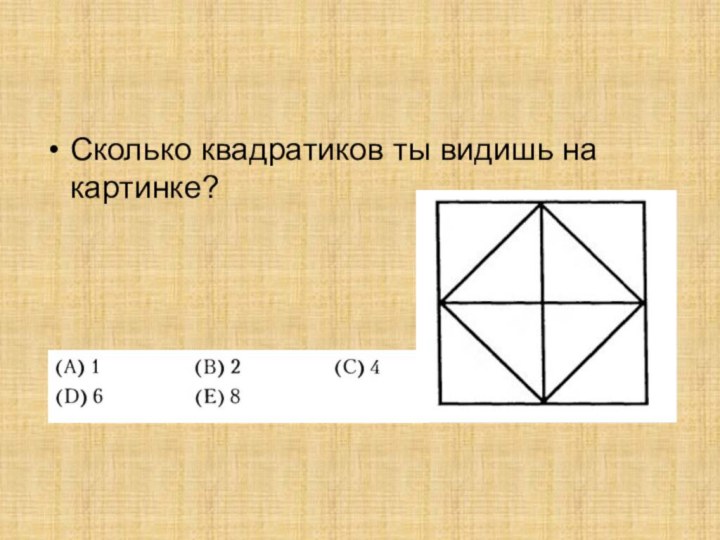
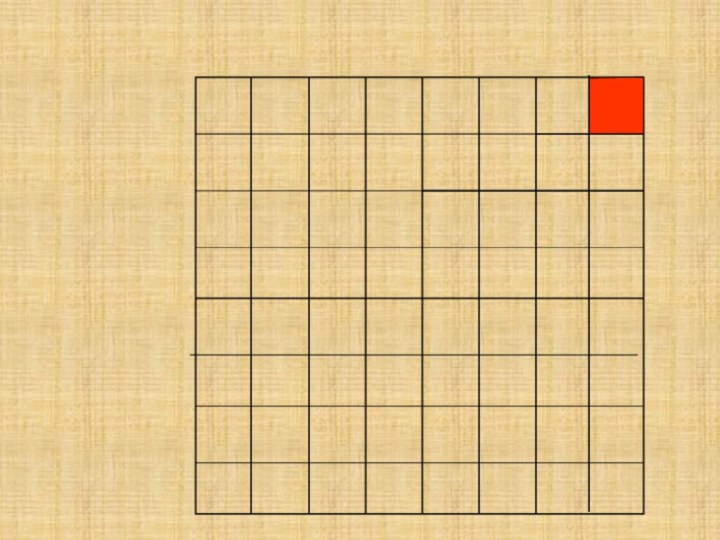
Сколько квадратиков ты видишь на картинке?
Слайд 13
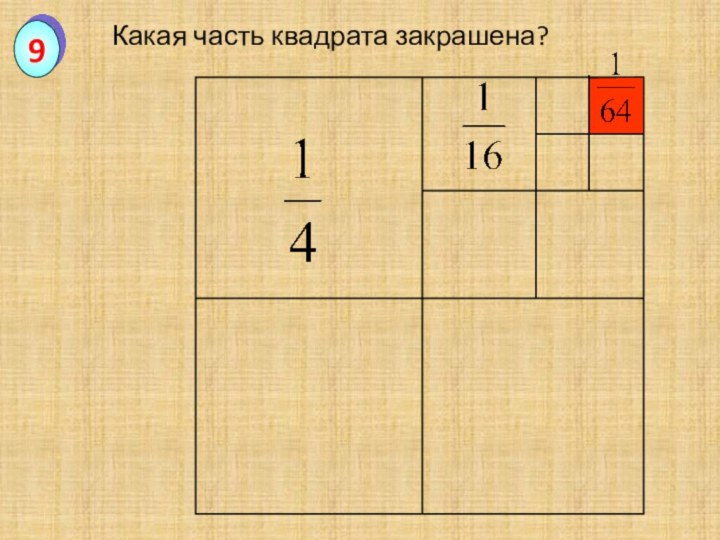
Какая часть квадрата закрашена?
9
Слайд 15
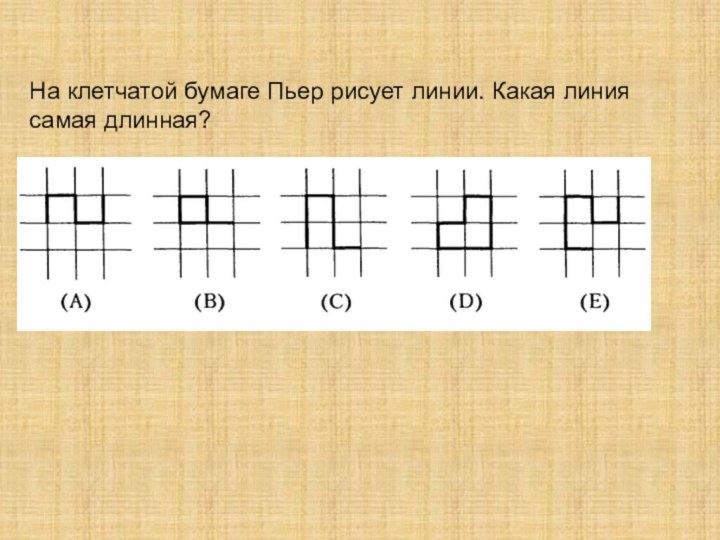
На клетчатой бумаге Пьер рисует линии. Какая линия
самая длинная?
Слайд 16
На рисунке закрашено 5 фигур.
Какая из них имеет
площадь не такую, как остальные?
Слайд 19
«Сущность вещей есть число, которое вносит во все
единство и гармонию»
«Все есть число»
Такие положения проповедовали
древнегреческий
математик Пифагор и его ученики пифагорейцы
Слайд 20
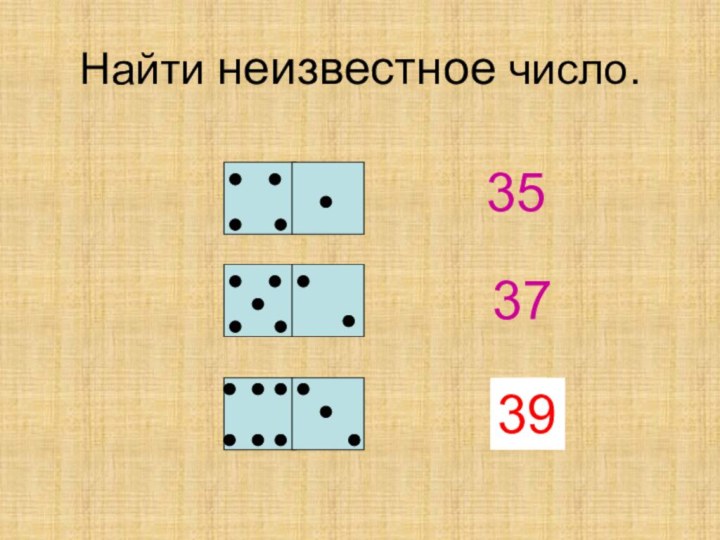
Найти неизвестное число.
35
37
?
39
Слайд 21
Найти неизвестные числа
35 8х-
3 = 21 4х- 8 = 12
61 3х+ 9 = ? 9- х = ?
27
8
Слайд 23
Найти неизвестное слово
Парк 13х- 5 =
47 пар
Удача 10- 7х = ?
дача
3
Слайд 24
Найти неизвестное слово
Приток х > 3
ток
Постель х < 5 ?
пост
Слайд 25
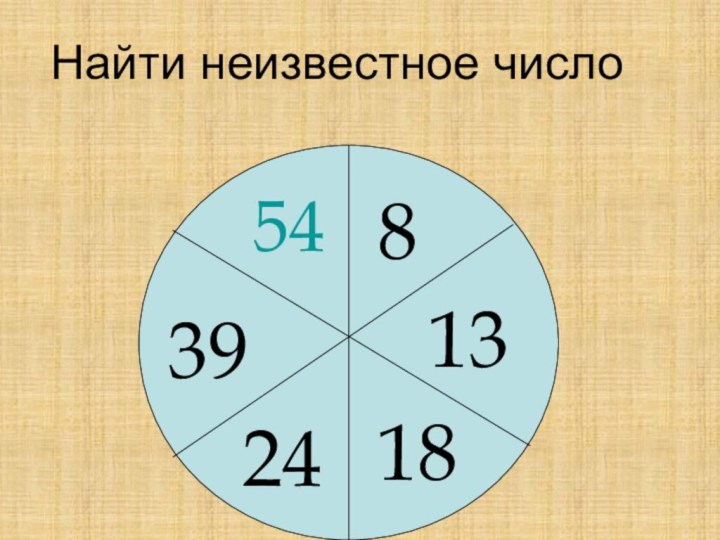
Найти неизвестное число
8
13
18
24
39
?
54
Слайд 26
«Скажи мне, и я забуду,
покажи мне, и
я, может быть, запомню,
вовлеки меня, и я пойму.»
Конфуций
Конфуций
(450г. до н.э.)
Слайд 27
Задача про гусеницу
Придумал ее Эдуард Люк и опубликовал
в
математических развлечениях в 1883 году.
В один прекрасный день,
ровно в 6 утра, гусеница вздумала забраться на вершину дерева высотой 12 футов. За день она успела подняться на 4 фута, а ночью во сне сползала вниз на 3 фута. Когда гусеница достигнет вершины дерева.
Слайд 28
Задача про червяка
Роскошно липа расцветала
Под ней червяк
завелся малый
Да вверх пополз он во всю мочь-
Четыре локтя делал в ночь,
Но днем со слепу полз обратно
Он на два локтя аккуратно
Трудился наш червяк отважный
И вот итог работы важной,
Награда девяти ночей;
Он на верхушке липы сей-
- Теперь, мой друг, поведай!
Какой та липа высоты.
Слайд 29
Задача заключается не в том, чтобы учить
математике, а в том, чтобы при посредстве математики дисциплинировать
ум.
В.Шрадер