случае промаха стрелок делает второй выстрел по той же
мишени. Вероятность попасть в мишень при одном выстреле равна 0,6. Найдите вероятность того, что мишень будет поражена (одним из выстрелов).
*
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть
















*
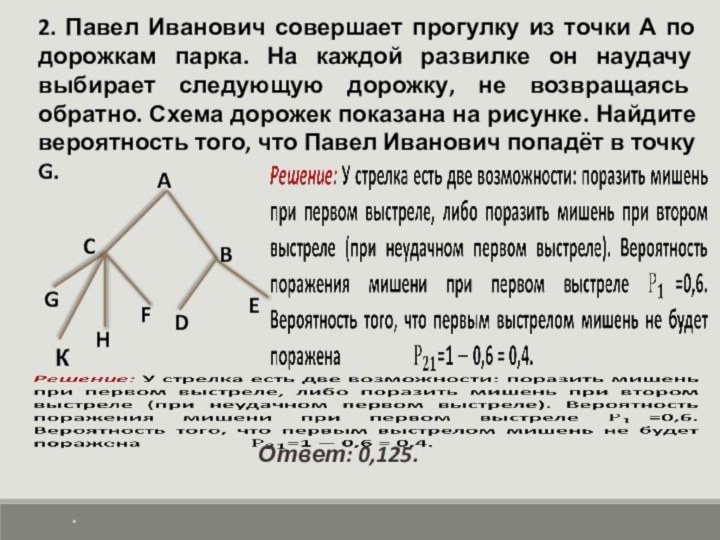
Ответ: 0,125.
*
Ответ: 0,0625.
*
Ответ: 0,1.
*
Ответ: 0,125.
*
Ответ: 0,025.
*
Ответ: 0,034.
*
*
Решение: Первый способ. Обозначим через А событие «кофе закончится в первом автомате», через В событие «кофе закончится во втором автомате». Событие С «кофе закончится хотя бы в одном автомате» является их суммой С = А + В.
*
*
Например, выигрыш, ничейный исход и проигрыш одного игрока в одной партии в шахматы – три несовместных события.
Теорема. Вероятность суммы двух несовместных событий A и B (появление хотя бы одного события) равна сумме вероятностей этих событий: P (A+B)=P(A) +P(B).
Теорема обобщается на любое число попарно несовместных событий
*
Определение. События называют совместными, если они могут происходить одновременно. Например, при бросании двух монет выпадение решки на одной не исключает появление решки на другой монете.
Теорема. Вероятность суммы двух совместных событий A и B (появление хотя бы одного события) равна сумме их вероятностей без вероятности их совместного появления, то есть P (A+B)=P(A) +P(B) – P(AB).
*