Слайд 2
Цели проекта:
1. Найти как можно
больше решений головоломки «Пентамино» для прямоугольника 6х10.
2. Создать банк найденных решений.
Гипотеза:
Поиск и систематизацию решений «Пентамино 6х10» можно ускорить, если применить специальные методы и приёмы.
Задачи:
1. Исследование методов поиска решений задачи «Пентамино 6х10».
2. Поиск способов систематизации найденных решений.
Слайд 4
История этих игр берет свое начало в 1953
году, когда американский математик Соломон Вольф Голомб (род. в
1932 г.) сделал доклад в Гарвардском математическом клубе «Шахматные доски и полимино».
Игры и задачи быстро увлекли не только школьников и студентов, но и профессоров математики.
Полимино
Слайд 5
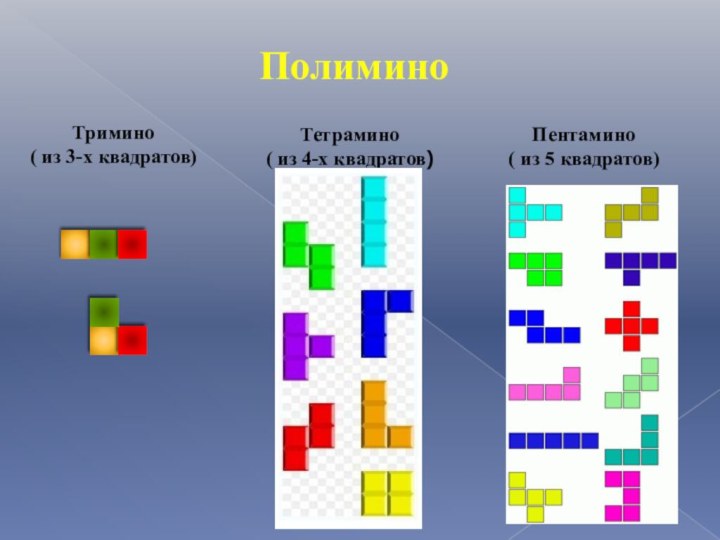
Полимино
Тетрамино
( из 4-х квадратов)
Пентамино
( из 5
квадратов)
Тримино
( из 3-х квадратов)
Слайд 6
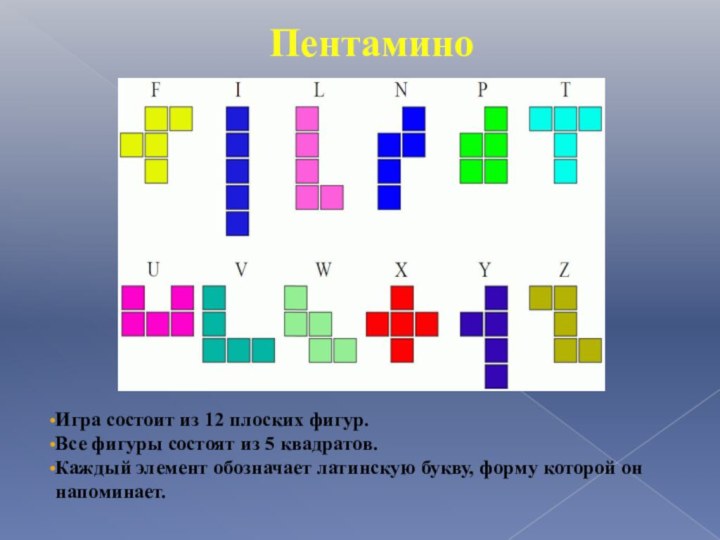
Игра состоит из 12 плоских фигур.
Все фигуры
состоят из 5 квадратов.
Каждый элемент обозначает латинскую букву,
форму которой он напоминает.
Пентамино
Слайд 7
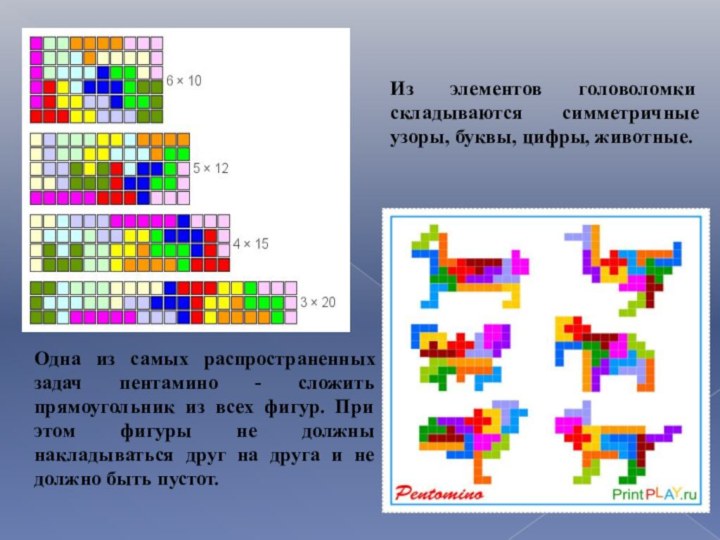
Одна из самых распространенных задач пентамино - сложить
прямоугольник из всех фигур. При этом фигуры не должны
накладываться друг на друга и не должно быть пустот.
Из элементов головоломки складываются симметричные узоры, буквы, цифры, животные.
Слайд 8
Пентамино 6х10
Условие задачи:
Всеми фигурами пентамино покрыть прямоугольник 6х10,
не накладывая фигуры друг на друга и используя каждую
фигуру один раз.
Существует 2339 различных укладок пентамино в прямоугольник 6×10.
Все способы решения этой задачи нашёл в 1965 году Джон Флетчер.
Слайд 9
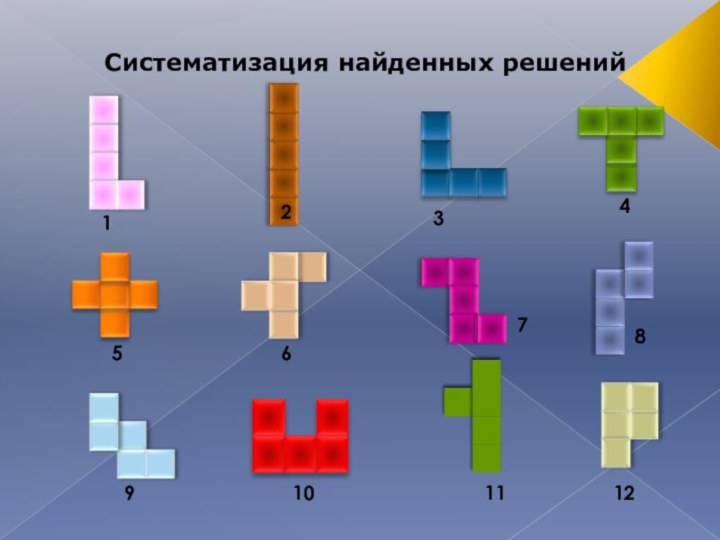
Систематизация найденных решений
1
2
3
4
5
6
7
8
9
10
11
12
Слайд 10
Систематизация найденных решений
1
12
1,2,3,4,5,6,7,8,9,10,11,12
Слайд 12
Равные комбинации, которые можно составить
разными способами из
одних и тех же фигур
Равные комбинации, которые можно составить
разными способами из разных фигур
Слайд 13
1
12
1) 1,2,3,4,5,6,7,8,9,10,11,12
Поиск нового решения
Слайд 14
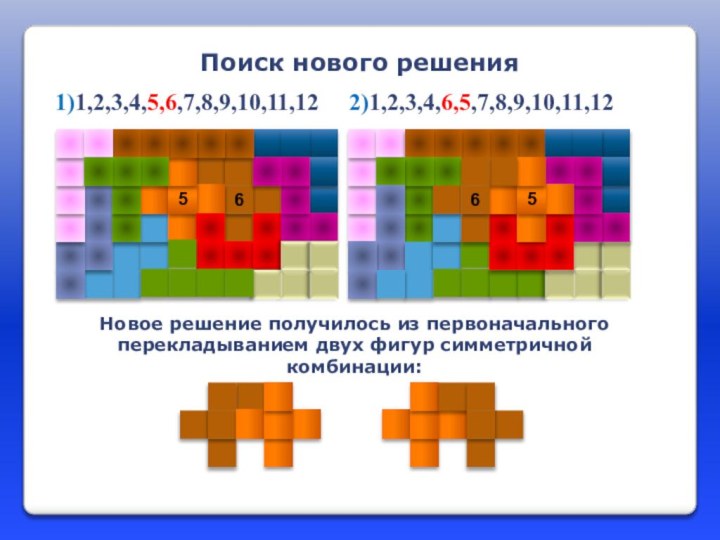
Поиск нового решения
Новое решение получилось из первоначального перекладыванием
двух фигур симметричной комбинации:
1)1,2,3,4,5,6,7,8,9,10,11,12 2)1,2,3,4,6,5,7,8,9,10,11,12
Слайд 15
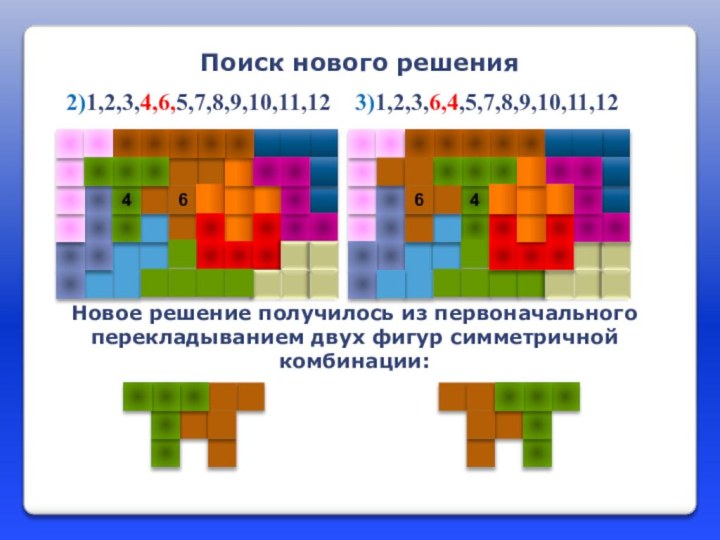
Новое решение получилось из первоначального перекладыванием двух фигур
симметричной комбинации:
Поиск нового решения
2)1,2,3,4,6,5,7,8,9,10,11,12 3)1,2,3,6,4,5,7,8,9,10,11,12
Слайд 16
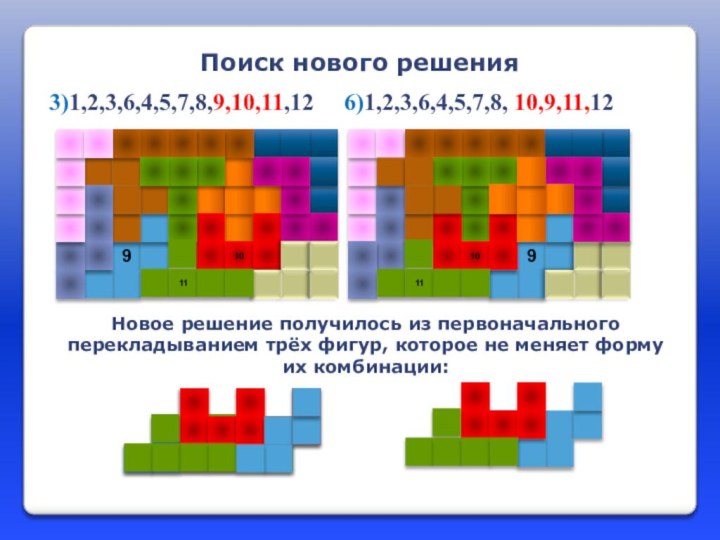
Новое решение получилось из первоначального перекладыванием трёх фигур,
которое не меняет форму их комбинации:
Поиск нового решения
3)1,2,3,6,4,5,7,8,9,10,11,12
6)1,2,3,6,4,5,7,8, 10,9,11,12
Слайд 17
Поиск нового решения
1)1,2,3,4,5,6,7,8,9,10,11,12 4)1,2,3,4,6,5,7,8,10,9,11,12
Новое решение получилось
из первоначального перекладыванием трёх фигур, которое не меняет форму
их комбинации:
Слайд 18
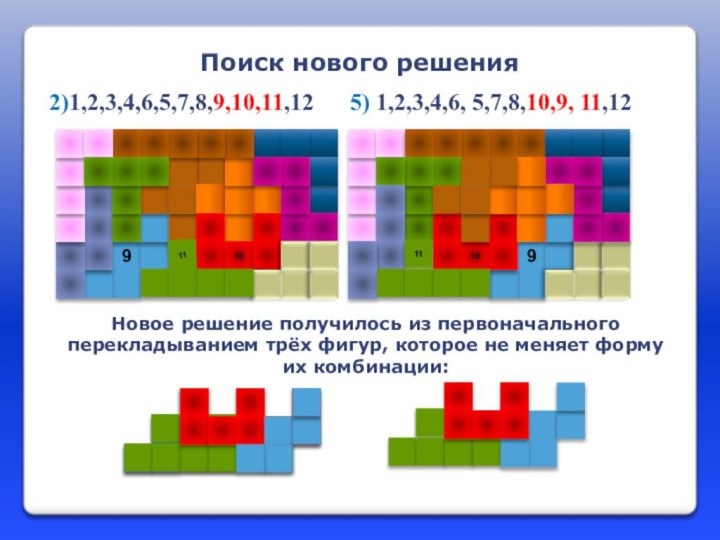
Новое решение получилось из первоначального перекладыванием трёх фигур,
которое не меняет форму их комбинации:
Поиск нового решения
2)1,2,3,4,6,5,7,8,9,10,11,12
5) 1,2,3,4,6, 5,7,8,10,9, 11,12
Слайд 19
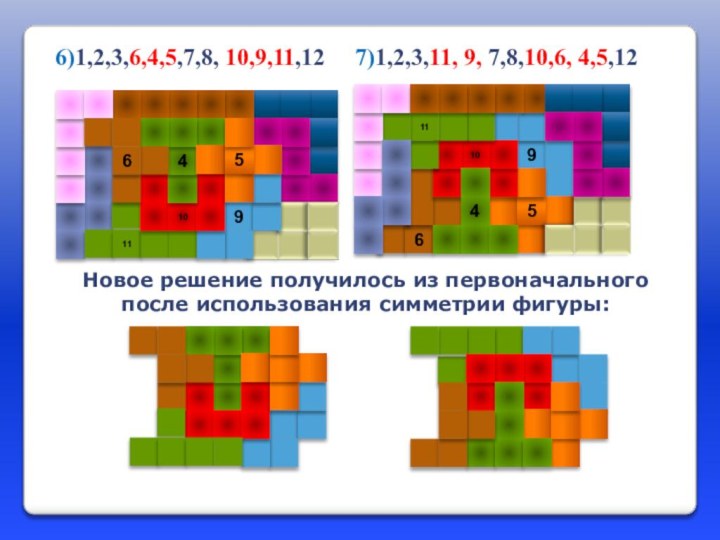
Новое решение получилось из первоначального после использования симметрии
фигуры:
6)1,2,3,6,4,5,7,8, 10,9,11,12 7)1,2,3,11, 9, 7,8,10,6, 4,5,12
Слайд 20
Результаты исследования
Гипотеза подтвердилась:
Поиск решений можно ускорить, если применить
методы, основанные на свойствах комбинаций фигур Пентамино – симметрия
и сохранение формы.
Найдено 87 решений !