- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Проект на тему: Математика на шахматной доске
Содержание
- 2. Каспаров и Карпов - лучшие шахматисты СССР
- 3. Проект на тему:
- 4. Цель проекта: рассмотреть основные аспекты взаимосвязи математики
- 5. Математика на шахматной доскеСистема координат;Четность и нечетность;Геометрия.1.Задача
- 6. Система координат Более чем за 100 лет
- 7. Система координатНа шахматной доске тоже есть координаты.
- 8. Чётность и нечётностьПри каждом ходе король меняет
- 9. Конь вышел на поле а8 и через
- 10. Геометрия шахматной доски Исход
- 11. Задачи на шахматной доске Задача
- 12. Задача Пусть требуется назначить n рабочих на
- 13. ЗадачаОколо каждой тюремной камеры можно поставить часового.
- 14. рассмотрели геометрию шахматной доски; выявили,
- 15. Скачать презентацию
- 16. Похожие презентации













Слайд 3
Проект на тему: «Математика на шахматной доске»
ФГБОУ
ВО «Курский государственный университет»
Факультет физики, математики, информатики
Научно - практическая
конференция«Проектный метод - мой первый шаг в науку»
Выполнила: Курасова Лилия ,
ОБПОУ «КГТТС»
1 тов «А»
Преподаватель математики:
Чухаева Е.В.
Слайд 4 Цель проекта: рассмотреть основные аспекты взаимосвязи математики и
игры в шахматы.
Задачи:
рассмотреть геометрию шахматной доски;
выявить, какую
роль играют шахматы в математике, через рассмотрение задач о шахматной доске;выяснить, какую роль играет математика в шахматах, через рассмотрение задач, связанных с шахматными фигурами.
Слайд 5
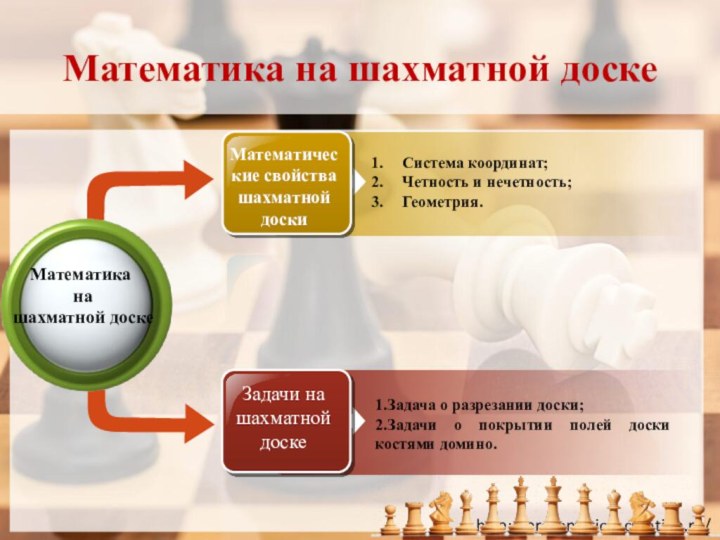
Математика на шахматной доске
Система координат;
Четность и нечетность;
Геометрия.
1.Задача о
разрезании доски;
2.Задачи о покрытии полей доски костями домино.
Математические свойства
шахматной доскиЗадачи на шахматной доске
Математика
на
шахматной доске
Слайд 6
Система координат
Более чем за 100 лет Гиппарх
предложил опоясать на карте земной шар параллелями и меридианами
и ввести хорошо теперь известные географические координаты: широту и долготу – и обозначить их числами.В ХIV в. Н. Оресм предложил покрыть плоскость прямоугольной сеткой и называть широтой и долготой то, что мы теперь называем абсциссой и ординатой.
-
Греческий ученый Гиппарх
Французский математик Н. Оресм
Французский математик, физик, философ Рене Декарт
Основная заслуга в создании метода координат принадлежит математику Р. Декарту.
Слайд 7
Система координат
На шахматной доске тоже есть координаты.
Горизонтали
(Ох) обозначаются латинскими буквами,
а вертикали (Оу) – цифрами.
Слайд 8
Чётность и нечётность
При каждом ходе король меняет четность
хода.
Например, первый ход – нечётный, второй – чётный
и т.д. Одновременно с этим король меняет цвет клетки, на которой он стоит.Слайд 9 Конь вышел на поле а8 и через несколько
ходов вернулся на него. Докажите, что он сделал четное
число ходов.Задача на четность, нечётность
Доказательство:
Делая каждый ход, конь меняет цвет клетки, на которой он стоит. Следовательно, каждый нечетный ход конь будет вставать на чёрную клетку. Исходя из этого и зная то, что конь должен вернуться на клетку а8, белого цвета, мы можем сказать, что он вернется через четное число ходов.
Слайд 10
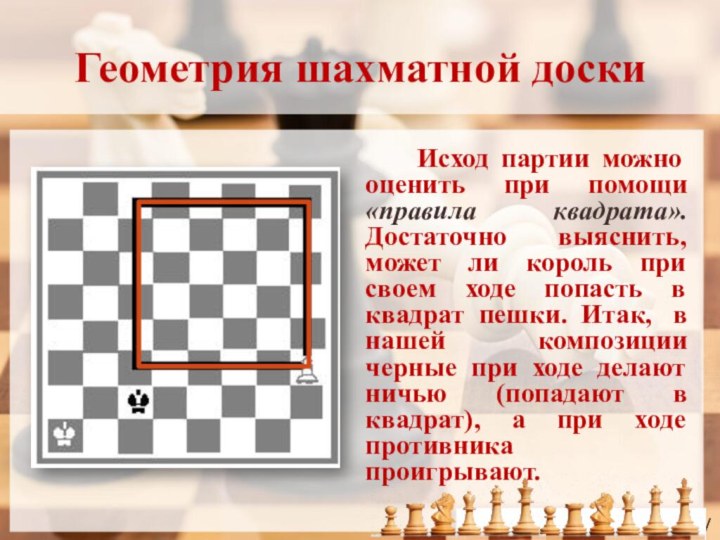
Геометрия шахматной доски
Исход партии
можно оценить при помощи «правила квадрата». Достаточно выяснить,
может ли король при своем ходе попасть в квадрат пешки. Итак, в нашей композиции черные при ходе делают ничью (попадают в квадрат), а при ходе противника проигрывают.
Слайд 11
Задачи на шахматной доске
Задача
Один восточный
властелин был таким искусным игроком, что за всю жизнь
потерпел всего четыре поражения. В честь своих победителей, четырех мудрецов, он приказал вставить в его шахматную доску четыре алмаза - на те поля, на которых был заматован его король (вместо алмазов изображены кони). После смерти властелина его сын, слабый игрок и жестокий деспот, решил отомстить мудрецам, обыгравшим его отца. Он велел разделить им шахматную доску с алмазами на четыре одинаковые по форме части так, чтобы каждая заключала в себе по одному алмазу.
Слайд 12
Задача
Пусть требуется назначить n рабочих на n
различных работ, причём каждая работа должна выполняться одним рабочим.
Сколькими способами можно сделать это назначение?Задачи на шахматной доске
Слайд 13
Задача
Около каждой тюремной камеры можно поставить часового. Находясь
у одной из камер, часовой видит, что происходит в
некоторых других, от которых к данной ведут коридоры. Каково наименьшее число часовых, необходимое для наблюдения за всеми камерами?Задачи на шахматной доске
Слайд 14
рассмотрели геометрию шахматной доски;
выявили, какую роль
играют шахматы в математике,
через рассмотрение задач о шахматной доске;
выяснили, какую роль играет математика в шахматах,
через рассмотрение задач , связанных с шахматными фигурами.
Выводы: