- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Зеркальная симметрия
Содержание
- 2. Симметрия - это гармония в расположении одинаковых предметов какой-либо
- 3. Виды симметрииа) Лучевая симметрия б) Осевая симметрияв) Центральная симметрияг) Зеркальная симметрия
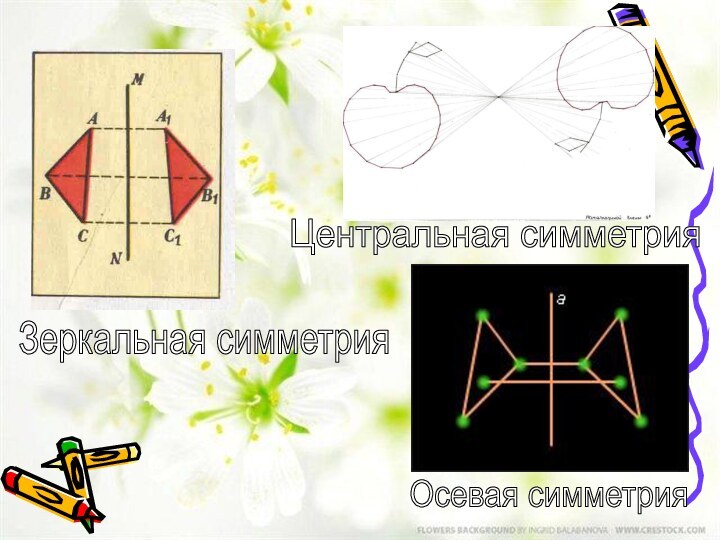
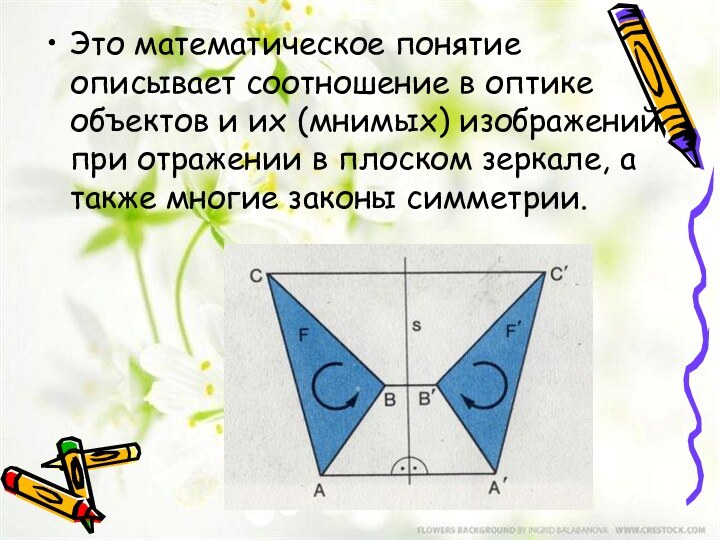
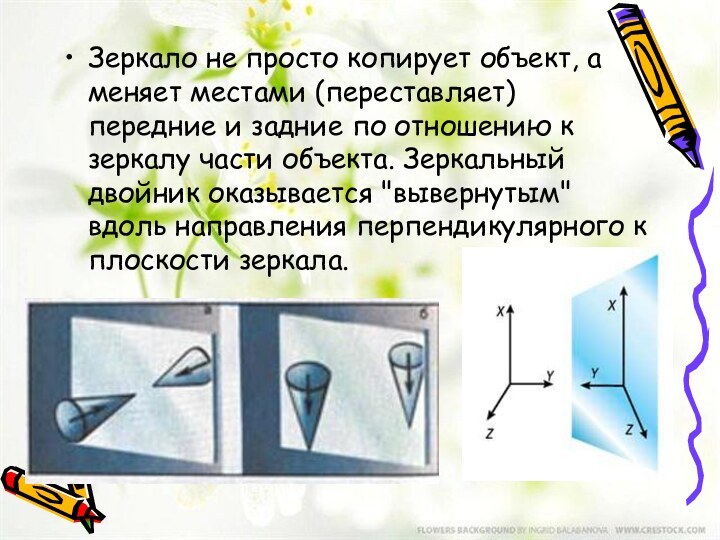
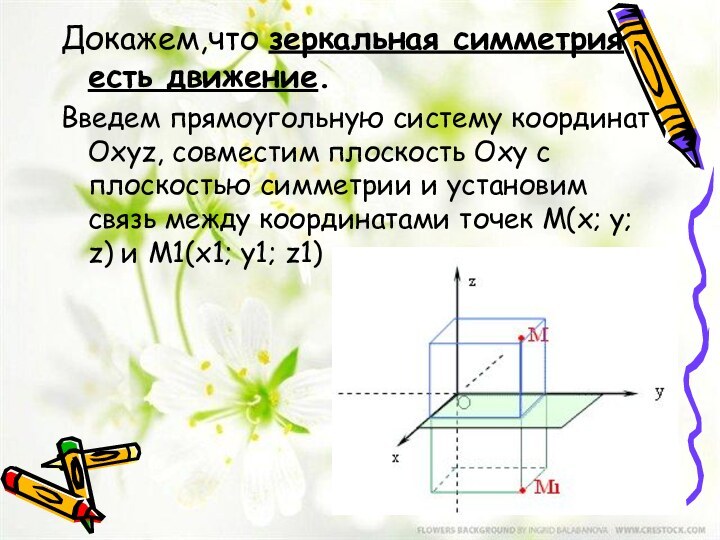
- 4. Зеркальная симметрияЦентральная симметрияОсевая симметрия
- 5. Зеркальной симметрией называется такое отображение пространства на
- 6. Это математическое понятие описывает соотношение в оптике
- 7. Геометрическая фигура называется симметричной относительно плоскости S ( рис.104 ), если для каждой
- 8. Зеркало не просто копирует объект, а меняет
- 9. Докажем,что зеркальная симметрия есть движение.Введем прямоугольную систему координат
- 10. Если М не лежит в плоскости Оху,
- 11. Зеркально осевая симметрия. Если плоская фигура ABCDE ( рис.107 ) симметрична
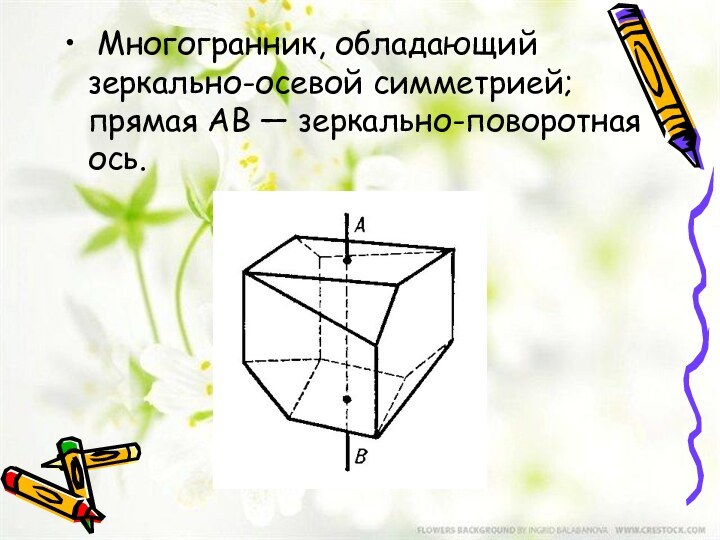
- 12. Многогранник, обладающий зеркально-осевой симметрией; прямая AB — зеркально-поворотная ось.
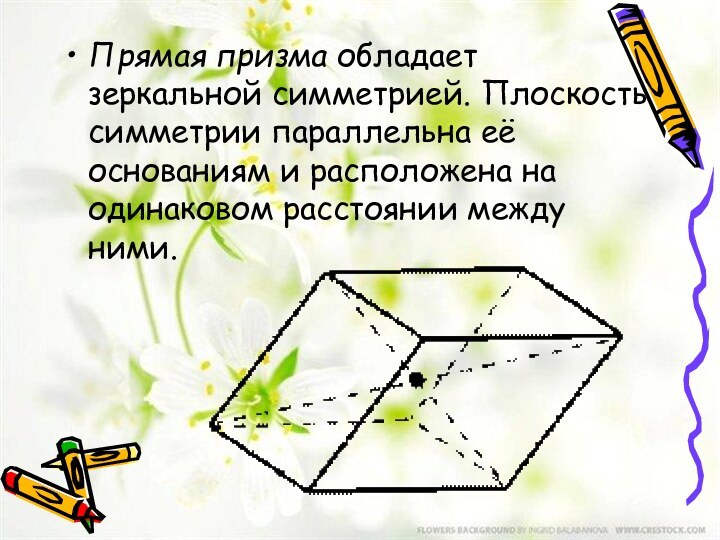
- 13. Прямая призма обладает зеркальной симметрией. Плоскость симметрии параллельна её основаниям и расположена на одинаковом расстоянии между ними.
- 14. Каждая деталь в симметричной системе существует
- 15. Зеркальная симметрия-это симметрия окружающего нас мира. Построение
- 16. Скачать презентацию
- 17. Похожие презентации
Симметрия - это гармония в расположении одинаковых предметов какой-либо группы или частей в одном предмете, причем расположение определяется одной или несколькими воображаемыми зеркальными плоскостями.
Слайд 3
Виды симметрии
а) Лучевая симметрия
б) Осевая симметрия
в) Центральная симметрия
г) Зеркальная симметрия
Слайд 5 Зеркальной симметрией называется такое отображение пространства на себя,
при котором любая точка М переходит в симметричную ей
относительно этой плоскости точку М1.ММ
м
М
М
М1
О
О
М
М
К
К
ОМ=ОМ1 ; ММ1
МК=М1К1
М1
К1
Слайд 6 Это математическое понятие описывает соотношение в оптике объектов
и их (мнимых) изображений при отражении в плоском зеркале,
а также многие законы симметрии.Слайд 7 Геометрическая фигура называется симметричной относительно плоскости S ( рис.104 ), если для каждой точки E этой
фигуры может быть найдена точка E1 этой же фигуры, так что отрезок EE1 перпендикулярен плоскости S и делится этой плоскостью
пополам ( EA = AE1 ). Плоскость S называется плоскостью симметрии. Симметричные фигуры, предметы и тела не равны друг другу в узком смысле слова. Они называются зеркально равными.Слайд 8 Зеркало не просто копирует объект, а меняет местами
(переставляет) передние и задние по отношению к зеркалу части
объекта. Зеркальный двойник оказывается "вывернутым" вдоль направления перпендикулярного к плоскости зеркала.
Слайд 9
Докажем,что зеркальная симметрия есть движение.
Введем прямоугольную систему координат Оxyz,
совместим плоскость Оxy с плоскостью симметрии и установим связь
между координатами точек M(x; y; z) и M1(x1; y1; z1)Слайд 10 Если М не лежит в плоскости Оху, то
х =х1, у =у1, z = -z1.
Если М I
Оху , то x=x1, y=y1, z=z1=0Рассмотрим А(x1; y1; z1), В(x2; y2; z2), А—> А1, В—> В1 , тогда А1(x1; y1; -z1), В1(x2; y2; -z2), тогда
АВ=А1В1, т.е.Оху – движение.
Слайд 11
Зеркально осевая симметрия.
Если плоская фигура ABCDE ( рис.107 ) симметрична относительно
плоскости S
( что возможно, если только плоская фигура перпендикулярна плоскости S ), то прямая KL,
по которой эти
плоскости пересекаются, являетсяосью симметрии фигуры ABCDE. В этом случае фигура ABCDE называетсязеркально-симметричной. Слайд 12 Многогранник, обладающий зеркально-осевой симметрией; прямая AB — зеркально-поворотная
ось.
Слайд 13 Прямая призма обладает зеркальной симметрией. Плоскость симметрии параллельна её основаниям
и расположена на одинаковом расстоянии между ними.
Слайд 14 Каждая деталь в симметричной системе существует как
двойник своей обязательной паре, расположенной по другую сторону оси,
и благодаря двойственности отдельных элементов сооружение “читается” целиком даже при восприятии с одной стороны.Слайд 15 Зеркальная симметрия-это симметрия окружающего нас мира. Построение изображения
