с центром О. Угол АСВ равен 74°. Найдите угол
AOD. Ответ дайте в градусах.Ответ: 32.
- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему ОГЭ 2018. Задание №17 . задания и решения к ним.
Содержание
- 2. Задание 10. Отрезки АС и BD — диаметры
- 3. Задание 10. В треугольнике ABC известно, что АС
- 4. Задание 10. В треугольнике ABC известно, что АС
- 5. Задание 10. Найдите площадь квадрата, описанного около окружности
- 6. Задание 10. Найдите площадь квадрата, описанного около окружности радиуса 16, Ответ: 1024.
- 7. Задание 10. Касательные в точках А и В
- 8. Задание 10. Касательные в точках А и В
- 9. Задание 10. На окружности с центром О отмечены
- 10. Задание 10. На окружности с центром О отмечены
- 11. Задание 10. Четырёхугольник ABCD вписан в окружность. Угол
- 12. Задание 10. Четырехугольник ABCD вписан в окружность. Угол
- 13. Задание 10. Треугольник ABC вписан в окружность с
- 14. Скачать презентацию
- 15. Похожие презентации
Задание 10. Отрезки АС и BD — диаметры окружности с центром О. Угол АСВ равен 74°. Найдите угол AOD. Ответ дайте в градусах. Ответ: 32.
Слайд 3 Задание 10. В треугольнике ABC известно, что АС =
8, ВС = 15, угол С равен 90°. Найдите
радиус описанной около этого треугольника окружности.Решение.
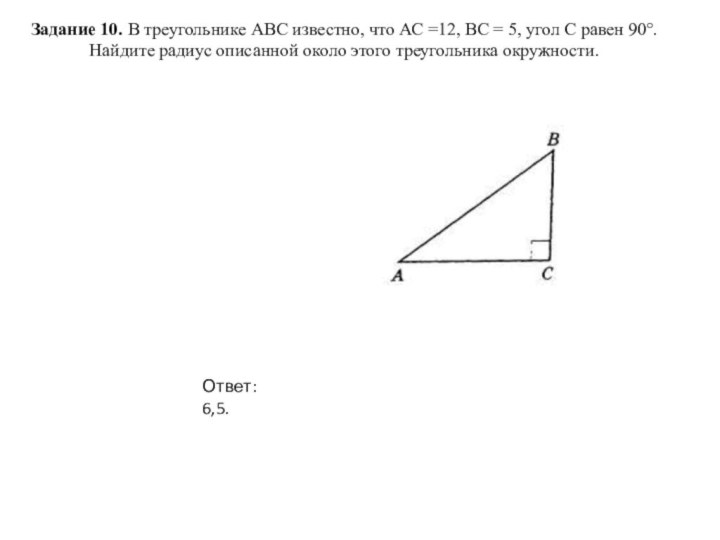
Радиус описанной вокруг прямоугольного треугольника окружности равен половине его гипотенузы. Найдем гипотенузу AB треугольника ABC по теореме Пифагора:
и радиус равен
.
Ответ: 8,5.
Слайд 4 Задание 10. В треугольнике ABC известно, что АС =12,
ВС = 5, угол С равен 90°. Найдите радиус
описанной около этого треугольника окружности.Ответ: 6,5.
Слайд 5 Задание 10. Найдите площадь квадрата, описанного около окружности радиуса
25.
Решение.
Из рисунка можно увидеть, что диаметр окружности (красная
линия) в точности равен длине стороны квадрата, то есть сторона квадрата равна.
Площадь квадрата определяется по формуле
и равна
.
Ответ: 2500.
Слайд 7 Задание 10. Касательные в точках А и В к
окружности с центром О пересекаются под углом 6°. Найдите
угол АВО. Ответ дайте в градусах.Решение.
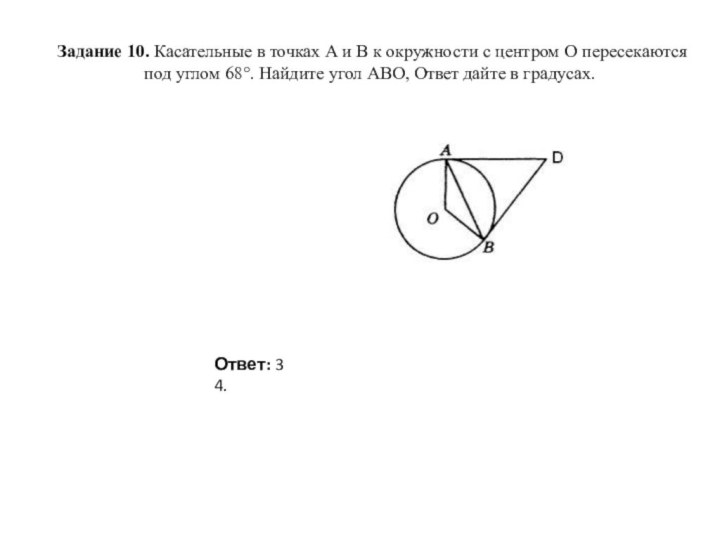
Рассмотрим четырехугольник ABDO, у которого угол (по условию задачи), а углы , так как они являются точками пересечения касательных и радиусов (касательная с радиусом, проведенным в точку касания, образуют прямой угол). Сумма углов в любом четырехугольнике равна 360 градусов, следовательно, последний угол , равен:
.
Теперь рассмотрим треугольник AOB, который является равнобедренным, так как AO=OB – радиусы окружности. Углы при основании равнобедренного треугольника равны, то есть , и, учитывая, что сумма углов в треугольнике равна 180 градусов, имеем:
.
Ответ: 3.
Слайд 8 Задание 10. Касательные в точках А и В к
окружности с центром О пересекаются под углом 68°. Найдите
угол АВО, Ответ дайте в градусах.Ответ: 34.
Слайд 9 Задание 10. На окружности с центром О отмечены точки
А и В так, что угол AOB = 66°.
Длина меньшей дуги АВ равна 99. Найдите длину большей дуги АВ.Решение.
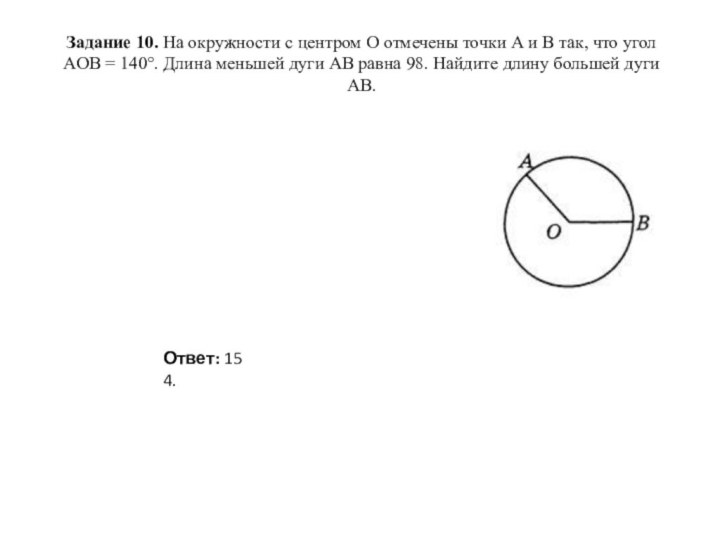
Длина всей окружности определяется по формуле . Примем за 1 градус дуги величину части окружности (так как в круге 360 градусов), тогда длина дуги в n° , будет равна
.
В задаче дан угол и длина дуги , найдем из формулы длины дуги радиус окружности:
.
Тогда длина большей дуги будет равна длине дуги в 360-66=294 градусов и составит величину
.
Ответ: 441.
Слайд 10 Задание 10. На окружности с центром О отмечены точки
А и В так, что угол AOB = 140°.
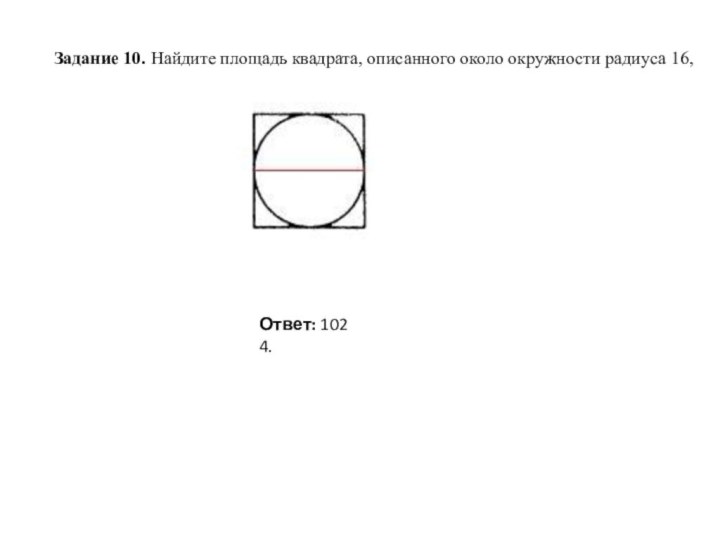
Длина меньшей дуги АВ равна 98. Найдите длину большей дуги АВ.Ответ: 154.
Слайд 11 Задание 10. Четырёхугольник ABCD вписан в окружность. Угол ABD
равен 85°, угол CAD равен 19°. Найдите угол ABC.
Ответ дайте в градусах.Решение.
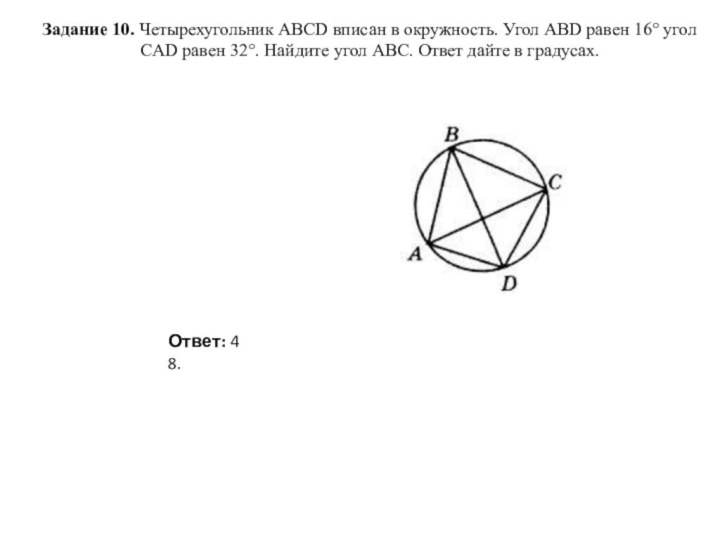
Угол ABC является вписанным углом, опирающимся на дугу AC. Как известно, градусная мера такого угла в два раза меньше градусной меры дуги, на которую он опирается. Найдем градусную меру дуги AC. Из рисунка видно, что AC=AD+DC. Градусные меры дуг AD и DC можно найти из углов ABD и CAD, получим:
Тогда
и угол
.
Ответ: 104.
Слайд 12 Задание 10. Четырехугольник ABCD вписан в окружность. Угол ABD
равен 16° угол CAD равен 32°. Найдите угол ABC.
Ответ дайте в градусах.Ответ: 48.
Слайд 13 Задание 10. Треугольник ABC вписан в окружность с центром
в точке О. Точки О и С лежат в
одной полуплоскости относительно прямой АВ. Найдите угол АСВ, если угол АОВ равен 167°. Ответ дайте в градусах.Решение.
Угол AOB является центральным, так как точка O – центр окружности, следовательно, градусная мера дуги AB равна также 167°. Угол ACB является вписанным в окружность углом и опирается на дугу AB. Известно, что величина вписанного угла равна половине градусной меры дуги, на которую он опирается, то есть
.
Ответ: 83,5.
