- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Табличный способ решения логических задач
Содержание
- 2. Эмблема мастер-класса: Говорят уравнение
- 3. Основные приемы и методы решения логических задач
- 4. Остановимся подробно на табличном способерешения логических задач
- 5. Решение логических задач табличным способомЗадача 1.В симфонический
- 6. Решение1. Смит самый высокий; 2. играющий на скрипке меньше ростом играющего на флейте; 0
- 7. Решение3. играющие на скрипке и флейте и Браун любят пиццу; 00
- 8. Решение4. когда между альтистом и трубачом возникает ссора, Смит мирит их; 00
- 9. Решение5. Браун не умеет играть ни на трубе, ни на гобое. 00110
- 10. РешениеТак как музыкантов трое, инструментов шесть и
- 11. Задача 2 На конгрессе встретились четверо ученых:
- 12. 1.Никто из учёных не владеет и французским,
- 13. Решение3. Историк говорит по-русски и может
- 14. Решение4. Физик, биолог и математик могут
- 15. Решение4. Физик, биолог и математик могут
- 16. Решение2. Хотя физик не говорит по-английски,
- 17. Алгоритм решения Составляйте таблицу, так как
- 18. Тренировочные задания Три одноклассника — Влад, Тимур
- 19. Ответ на задачу
- 20. Ответ на задачу
- 21. “Смотреть – не значит видеть!” k
- 22. Скачать презентацию
- 23. Похожие презентации

















Слайд 3
Основные приемы и методы решения логических задач
Теория,
мой друг, суха, но
зеленеет жизни древо.
И.В.Гете
Известно несколько различных способов решения логических задач: Метод рассуждений;
Метод таблиц;
Метод графов;
Метод блок-схем;
Метод бильярда;
Метод кругов Эйлера.
Слайд 5
Решение логических задач табличным способом
Задача 1.
В симфонический оркестр
приняли на работу трёх музыкантов: Брауна, Смита и Вессона,
умеющих играть на скрипке, флейте, альте, кларнете, гобое и трубе.Известно, что:
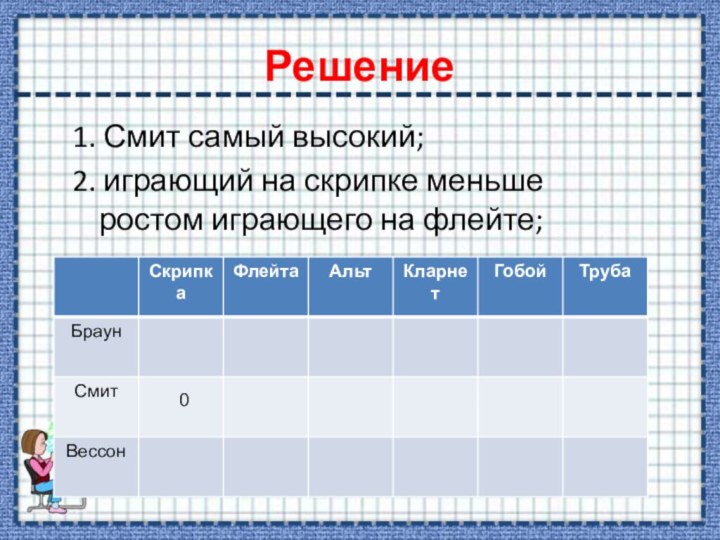
1. Смит самый высокий;
2. играющий на скрипке меньше ростом играющего на флейте;
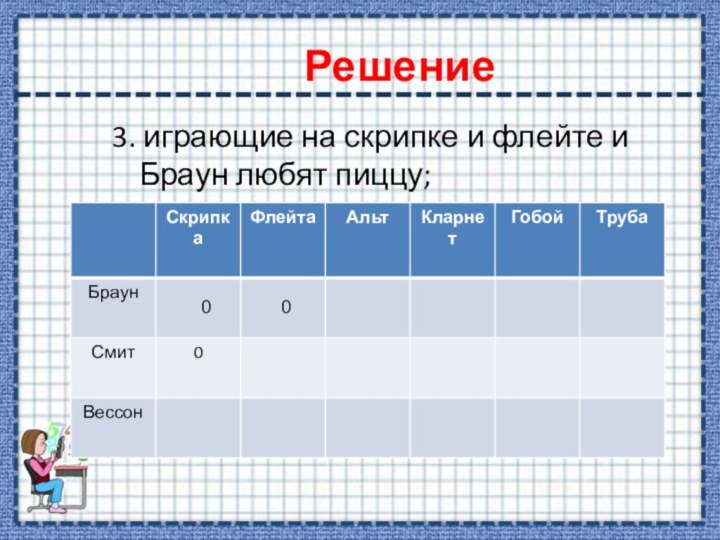
3. играющие на скрипке и флейте и Браун любят пиццу;
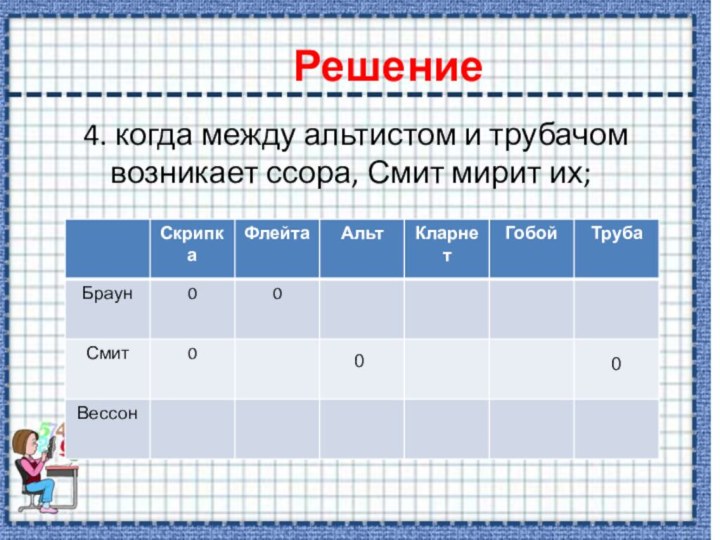
4. когда между альтистом и трубачом возникает ссора, Смит мирит их;
5. Браун не умеет играть ни на трубе, ни на гобое.
На каких инструментах играет каждый из музыкантов, если каждый владеет двумя инструментами?
Слайд 10
Решение
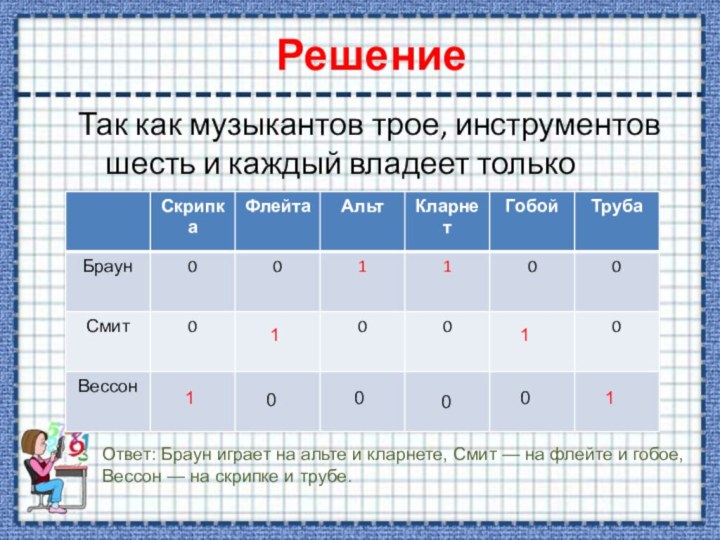
Так как музыкантов трое, инструментов шесть и каждый
владеет только двумя инструментами, получается, что каждый музыкант играет
на инструментах, которыми остальные не владеют.1
1
1
1
0
0
0
0
Ответ: Браун играет на альте и кларнете, Смит — на флейте и гобое,
Вессон — на скрипке и трубе.
Слайд 11
Задача 2
На конгрессе встретились четверо ученых: физик,
биолог, историк и математик. Каждый учёный владел двумя языками
из четырёх (русским, английским, французским и итальянским), но не было такого языка, на котором могли бы разговаривать все четверо. Есть только один язык, на котором могли вести беседу сразу трое.1.Никто из учёных не владеет и французским, и русским языками.
2. Хотя физик не говорит по-английски, он может служить переводчиком, если историк и биолог захотят побеседовать.
3. Историк говорит по-русски и может говорить с математиком, хотя тот не знает ни одного русского слова.
4. Физик, биолог и математик могут разговаривать на одном языке.
Какими двумя языками владеет каждый учёный?
Слайд 12 1.Никто из учёных не владеет и французским, и
русским языками.
2. Хотя физик не говорит по-английски, он
может служит переводчиком, если историк и биолог захотят побеседовать. Решение
0
Слайд 13
Решение
3. Историк говорит по-русски и может говорить с
математиком, хотя тот не знает ни одного русского слова.
4. Хотя физик не говорит по-английски, он может служить переводчиком, если историк и биолог захотят побеседовать.
0
1
1
0
Слайд 14
Решение
4. Физик, биолог и математик могут разговаривать на
одном языке.
1.Никто из учёных не владеет и французским,
и русским языками. 0
0
Слайд 15
Решение
4. Физик, биолог и математик могут разговаривать на
одном языке.
Какими двумя языками владеет каждый учёный?
1
1
1
1
Слайд 16
Решение
2. Хотя физик не говорит по-английски, он может
служить переводчиком, если историк и биолог захотят побеседовать.
3.
Историк говорит по-русски и может говорить с математиком, хотя тот не знает ни одного русского слова. 0
1
0
1
Ответ: математик – английский и итальянский; биолог – французский
и итальянский; физик – русский и итальянский; историк – русский и
английский.
Слайд 17
Алгоритм решения
Составляйте таблицу, так как в таблице
удаётся
учесть все возможные варианты.
2. Внимательно читайте каждое утверждение,
так как в каждом содержится что-то такое, что позволит вам
исключить хотя бы один из вариантов.
3. Старайтесь отыскать ключевое утверждение,
оно поможет развязать весь клубок.
4. После того как вы сравнили все утверждения и
исключили из них те, невероятность которых была на
поверхности, сравните утверждения между собой,
установите связи и противоречия.
5. Решение можно найти простым методом
последовательных исключений.
Слайд 18
Тренировочные задания
Три одноклассника — Влад, Тимур и
Юра, встретились спустя 10 лет после окончания школы. Выяснилось,
что один из них стал врачом, другой физиком, а третий юристом. Один полюбил туризм, другой бег, страсть третьего — регби.Юра сказал, что на туризм ему не хватает времени, хотя его сестра — единственный врач в семье, заядлый турист. Врач сказал, что он разделяет увлечение коллеги.
Забавно, но у двоих из друзей в названиях их профессий и увлечений не встречается ни одна буква их имен.
Определите, кто чем любит заниматься в свободное время и у кого какая профессия.





























