Презентация на тему Урок на тему Действия над векторами

теме «Действия над векторами».
Выявление связи геометрии с различными областями

человеческих знаний.
Развитие навыков использования векторов в математике и ее приложениях.

является началом, а какая - концом, называется направленным отрезком

или вектором.

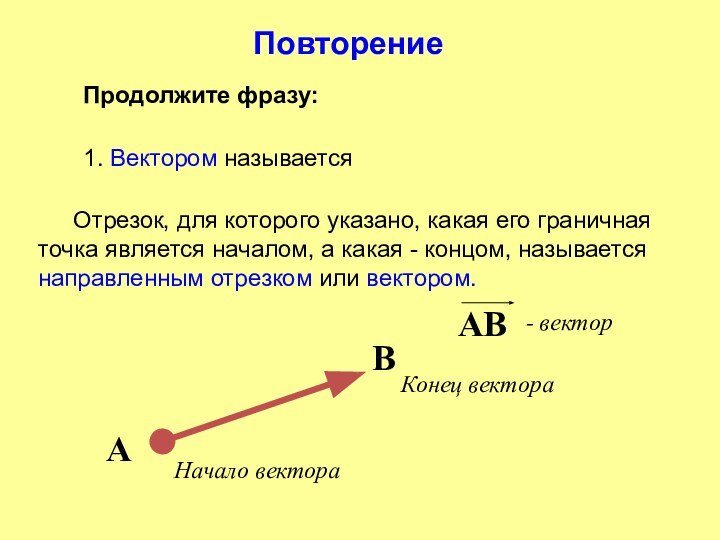
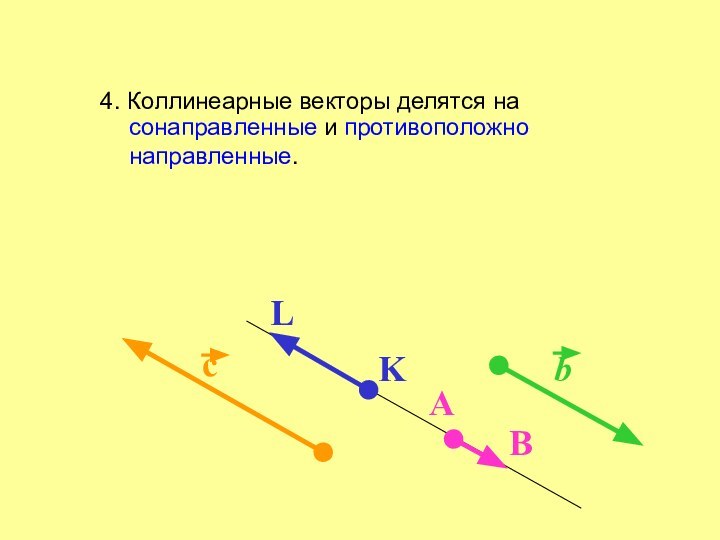
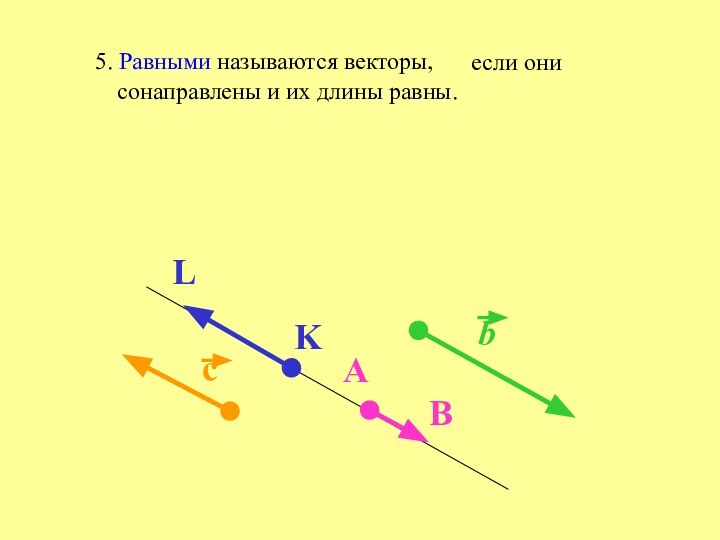
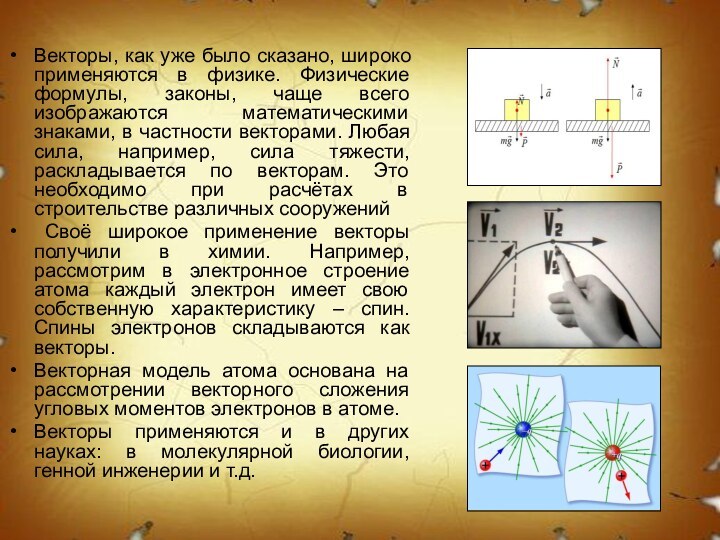
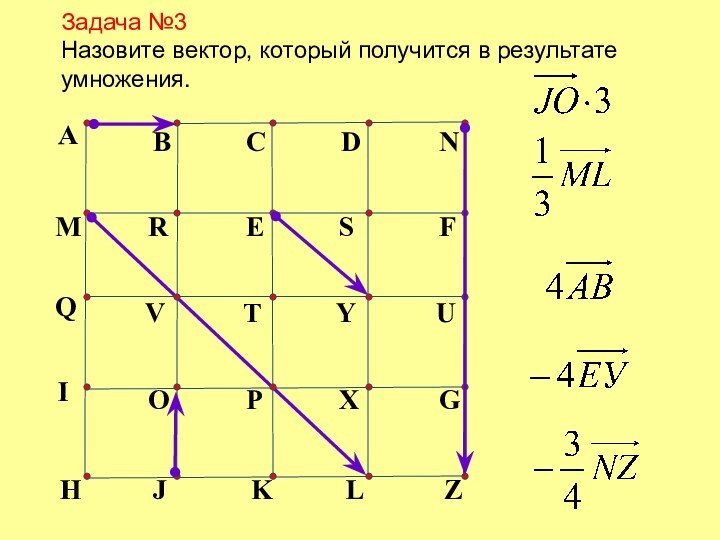
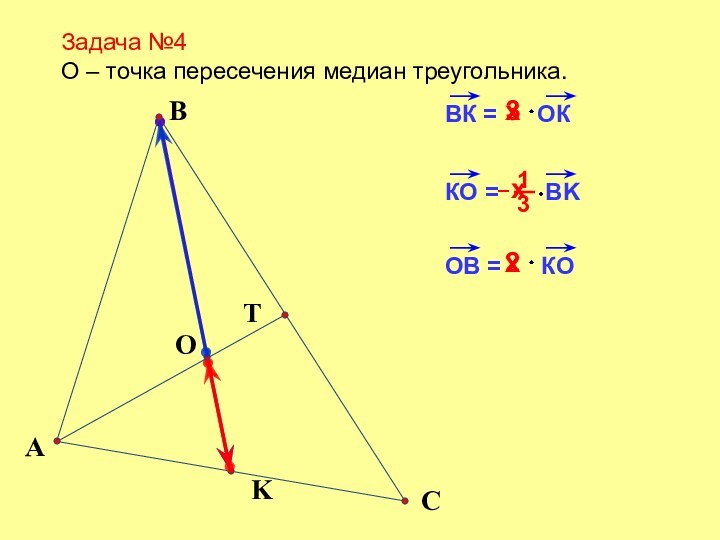
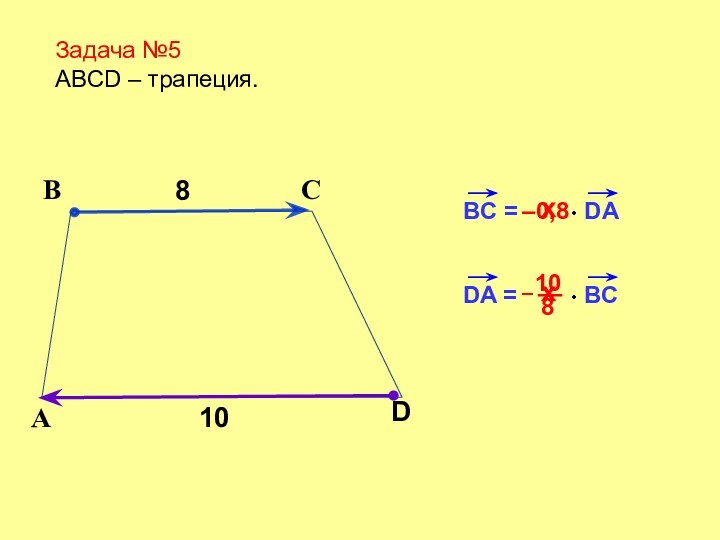
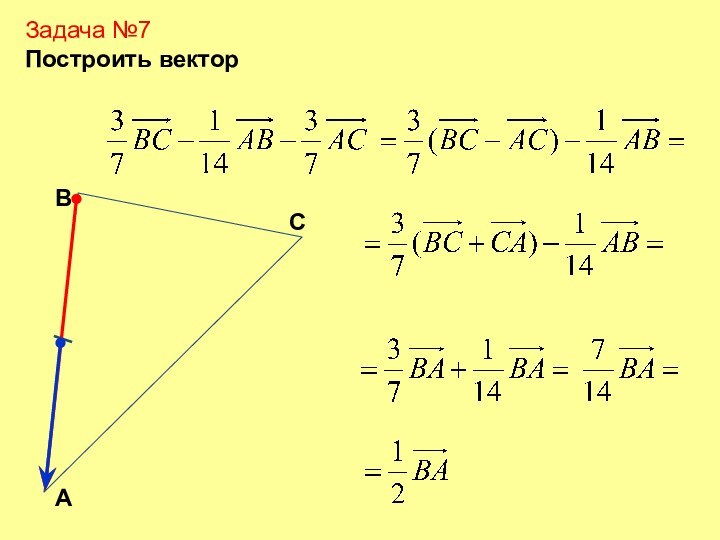
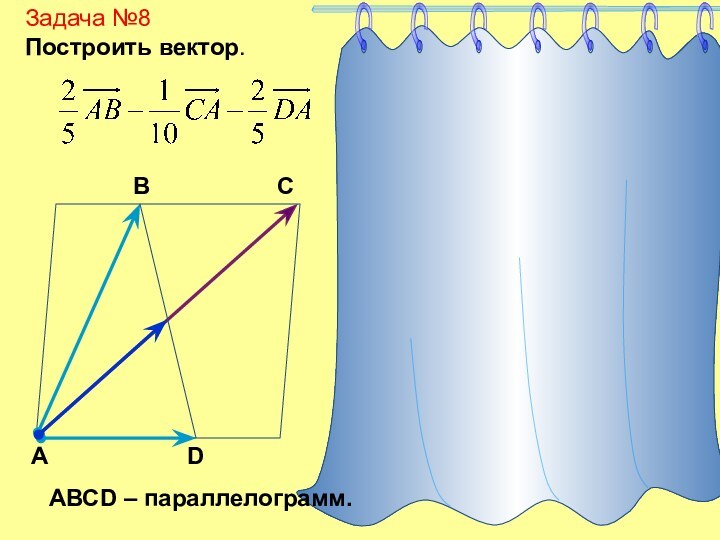
Конец вектора

Начало вектора

- вектор

Повторение

Продолжите фразу:

1. Вектором называется

отрезка.

называются коллинеарными,
если они лежат на одной прямой или

на параллельных прямых.

если они сонаправлены и их длины равны.

-точка пересечения диагоналей.
Найдите по данному рисунку:
пары коллинеарных векторов;
2)

пары сонаправленных векторов;

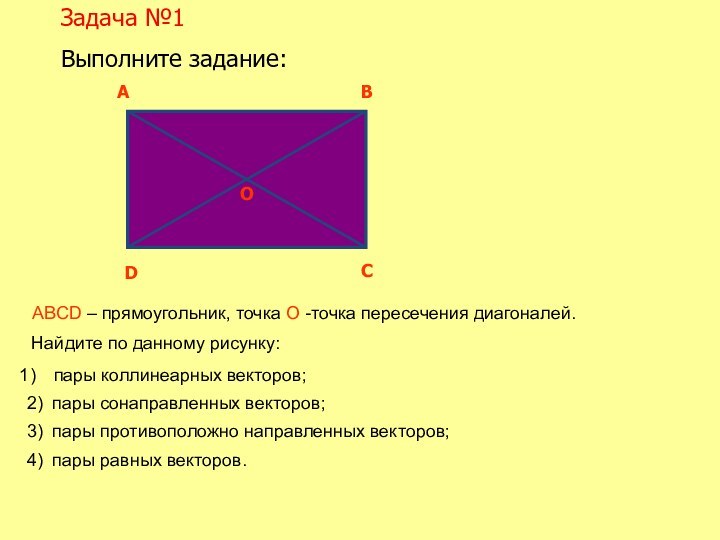
3) пары противоположно направленных векторов;

4) пары равных векторов.

английского математика и астронома Уильяма Гамильтона. Основы векторного исчисления

были заложены исследованиями английского математика У. Гамильтона и немецкого математика Г. Грассмана. Их идеи были использованы английским физиком Дж. К. Максвеллом в его работах по электричеству и магнетизму. Современный вид векторам придал американский физик Дж. Гиббс.

Уильям Гамильтон

признания. Например, английский ученый Тейт утверждал, что пользоваться векторами

неудобно.
Несмотря на это, после Гиббса векторы стали широко применять. Так, на использовании векторов основано изложение механики во многих английских учебниках.

Дж. Гиббс

Позже вектор использовался в элементах векторного анализа Гиббса, а затем Хэвисайд придал векторному анализу современный вид.

О.Т. Хэвисайд

физике. Физические формулы, законы, чаще всего изображаются математическими знаками,

в частности векторами. Любая сила, например, сила тяжести, раскладывается по векторам. Это необходимо при расчётах в строительстве различных сооружений
Своё широкое применение векторы получили в химии. Например, рассмотрим в электронное строение атома каждый электрон имеет свою собственную характеристику – спин. Спины электронов складываются как векторы.
Векторная модель атома основана на рассмотрении векторного сложения угловых моментов электронов в атоме.
Векторы применяются и в других науках: в молекулярной биологии, генной инженерии и т.д.

=AB+BC=AC

вектор.
Произведение нулевого вектора на любое число считается нулевой вектор.
3.

Умножение вектора на число

на число

,

. О – точка пересечения диагоналей. Выразите векторы , и через и .

= CK
х

х
4)NN = XD
х
5)ХТ =

XD

х

7)TX = XT

х

Самостоятельная работа
Найдите число x.

-4

0

x не сущ

1

-1

– трапеция.


А
D
10
х
–0,8
DA = BC
х

= 5 : 3

А
D
BS =

DA

х

S

х

: ЕС = 3 : 1,

К – середина

DC, АВ = , AD = . Выразите через

векторы и векторы:

С

А

В

D

и .
Постройте векторы

+ ; - ; 2 ; -3 .

и и углы, образуемые равнодействующей с силами

и , если = 4Н и = 6Н а φ =

Используя теорему косинусов, находим

По теореме синусов имеем


Следовательно,


Контрольные вычисления:

φ

φ

φ

вы сегодня познакомились?
2. Какие правила можно использовать для сложения

векторов?
3. Что получится при умножении вектора на число?

Итоги занятия

активно/пассивно
Своей работой на занятии

я доволен/не доволен
Занятие для меня показался коротким/длинным
За время занятия я не устал/ устал
Моё настроение стало лучше/стало хуже
Материал занятия мне был понятен/не понятен
полезен/не полезен
интересен /скучен
На занятии мне было интересно /не интересно

§2, №17, 19
Домашнее задание