Что такое findslide.org?

FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.

Для правообладателей

Обратная связь

Email: Нажмите что бы посмотреть

Презентация на тему по геометрии на тему: Многогранники.Тела и поверхности вращения

Содержание

2. «Многогранники. Тела и поверхности вращения»Обобщающий урок по теме:
3. Цель урока: углубление, обобщение,
4. Эпиграф к уроку:«Каждая
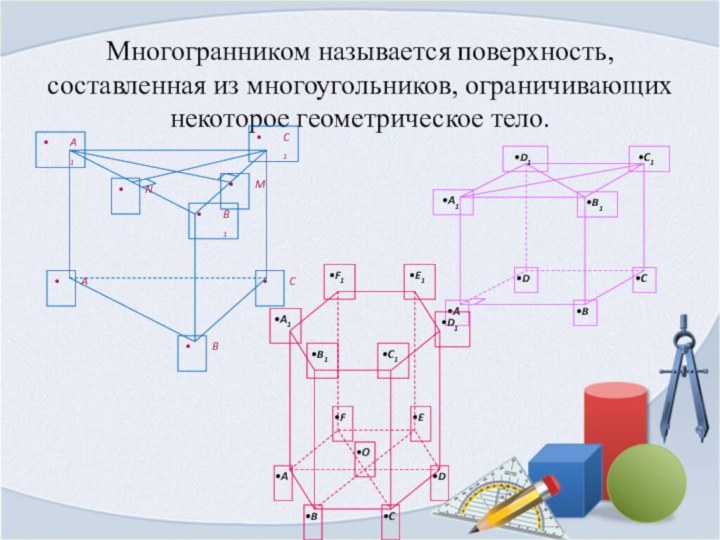
5. Многогранником называется поверхность, составленная из многоугольников, ограничивающих некоторое геометрическое тело.
6. Призма — многогранник, две грани которого
7. Параллелепипед Параллелепипед — призма, основанием которой служит параллелограмм, или (равносильно)
8. Куб Куб или правильный гексаэдр — правильный многогранник, каждая грань
9. Пирамида Пирамида — многогранник, основание которого —многоугольник, а остальные грани — треугольники, имеющие общую вершину.
10. Усеченная пирамида Усеченной пирамидой называется многогранник, у
11. ТЕЛА ВРАЩЕНИЯ Цилиндр Цилиндр — геометрическое тело,
12. Конус Конус – это тело, которое
13. Задание Приведите примеры из окружающего мира
14. ШарШаром называется тело, которое состоит из всех
15. Решение задач (работа в группах)I группа:
16. № 1196. Измерения прямоугольного параллелепипеда равны 8см,
17. ФизминуткаРисуй глазами треугольникРисуй глазами треугольник.Теперь его переверниВершиной
18. Решите задачу: Классное помещение должно быть таким,
19. Когда человеку уютно, приятно, спокойно, он говорит,
20. Эпиграф к уроку:«Каждая
21. - Комфортно ли вы себя
22. Домашнее задание: 1) повторить п.122-131; 2) решить
23. Если после сегодняшнего урока у вас остались
24. Скачать презентацию
25. Похожие презентации

«Многогранники. Тела и поверхности вращения»Обобщающий урок по теме:

Главная
Математика
Презентация по геометрии на тему: Многогранники.Тела и поверхности вращения

«Многогранники. Тела и поверхности вращения»Обобщающий урок по теме:

Цель урока: углубление, обобщение, систематизация, закрепление полученных знаний по

Эпиграф к уроку:«Каждая проблема, которую я решал, становилась

Многогранником называется поверхность, составленная из многоугольников, ограничивающих некоторое геометрическое тело.

Призма — многогранник, две грани которого являются равными многоугольниками, лежащими в

Параллелепипед Параллелепипед — призма, основанием которой служит параллелограмм, или (равносильно) многогранник, у которого шесть граней

Куб Куб или правильный гексаэдр — правильный многогранник, каждая грань которого представляет собой квадрат. Частный

Пирамида Пирамида — многогранник, основание которого —многоугольник, а остальные грани — треугольники, имеющие общую вершину.

Усеченная пирамида Усеченной пирамидой называется многогранник, у которого вершинами служат вершины основания

ТЕЛА ВРАЩЕНИЯ Цилиндр Цилиндр — геометрическое тело, ограниченное цилиндрической поверхностью и двумя

Конус Конус – это тело, которое описывает прямоугольный треугольник при вращении

Задание Приведите примеры из окружающего мира тел, похожих на тело полученное

ШарШаром называется тело, которое состоит из всех точек пространства, находящихся на расстоянии,

Решение задач (работа в группах)I группа: №1196 стр 315. II группа:

№ 1196. Измерения прямоугольного параллелепипеда равны 8см, 12см и 18см. Найдите ребро

ФизминуткаРисуй глазами треугольникРисуй глазами треугольник.Теперь его переверниВершиной вниз.И вновь глазамиты по периметру

Решите задачу: Классное помещение должно быть таким, чтобы на одного учащегося приходилось

Когда человеку уютно, приятно, спокойно, он говорит, что ему комфортно. Оказывается, комфортность

- Комфортно ли вы себя чувствовали на уроке? - Возникли

Домашнее задание: 1) повторить п.122-131; 2) решить №1189, №1214, 3) вычислить

Если после сегодняшнего урока у вас остались какие-то вопросы (острые углы), то

Слайды презентации

Слайд 2 «Многогранники. Тела и
поверхности вращения»
Обобщающий урок по теме:

Слайд 3 Цель урока: углубление, обобщение, систематизация, закрепление полученных знаний по

теме: «Многогранники. Тела и поверхности вращения» и их применение

при решении задач.

Слайд 4 Эпиграф к уроку:
«Каждая проблема,

Эпиграф к уроку:«Каждая проблема, которую я решал, становилась правилом,

которую я решал, становилась правилом, которое мне в последствии служило

для решения других проблем»
Рене Декарт

Слайд 5 Многогранником называется поверхность, составленная из многоугольников, ограничивающих некоторое

геометрическое тело.

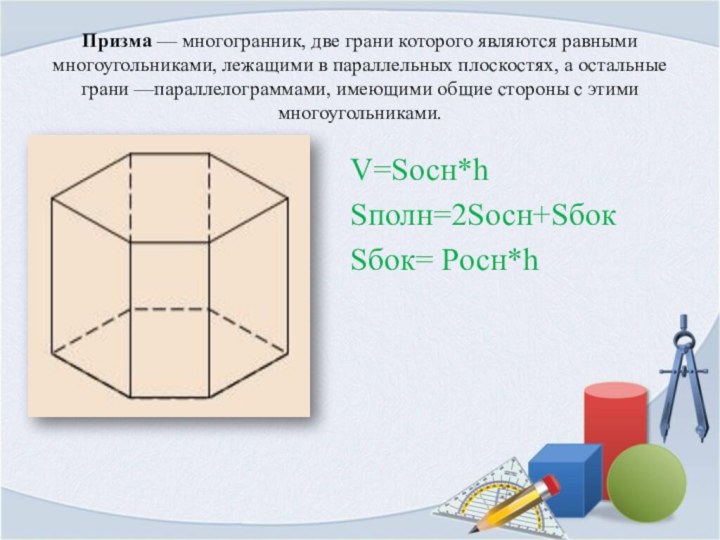
Слайд 6 Призма — многогранник, две грани которого являются равными многоугольниками, лежащими

в параллельных плоскостях, а остальные грани —параллелограммами, имеющими общие стороны

с этими многоугольниками.

V=Sосн*h
Sполн=2Sосн+Sбок
Sбок= Pосн*h

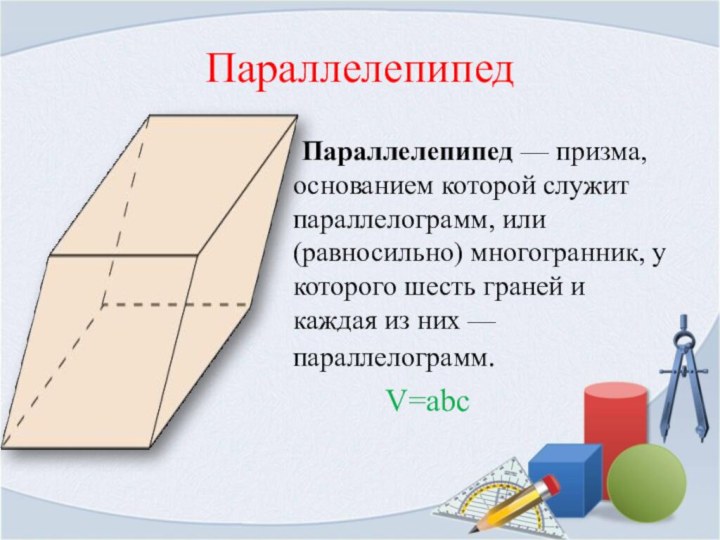
Слайд 7 Параллелепипед
Параллелепипед — призма, основанием которой служит параллелограмм, или (равносильно) многогранник,

Параллелепипед Параллелепипед — призма, основанием которой служит параллелограмм, или (равносильно) многогранник, у которого шесть

у которого шесть граней и каждая из них —

параллелограмм.
V=abc

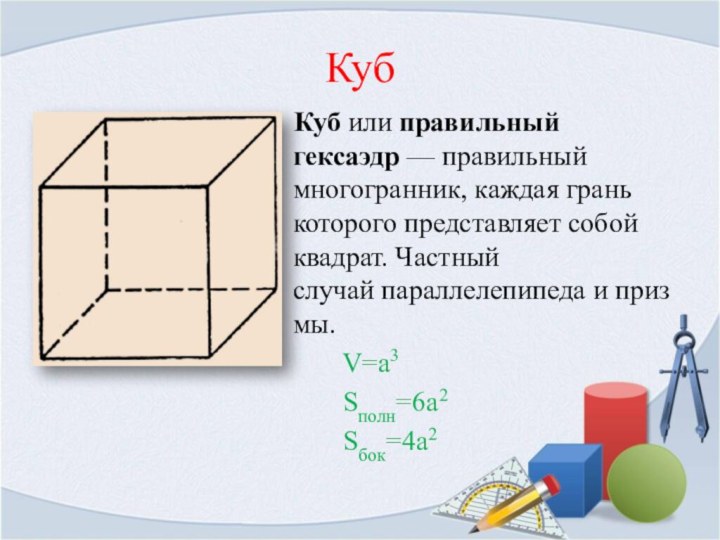
Слайд 8 Куб
Куб или правильный гексаэдр — правильный многогранник, каждая грань которого

представляет собой квадрат. Частный случай параллелепипеда и призмы.

V=a3
Sполн=6a2
Sбок=4a2

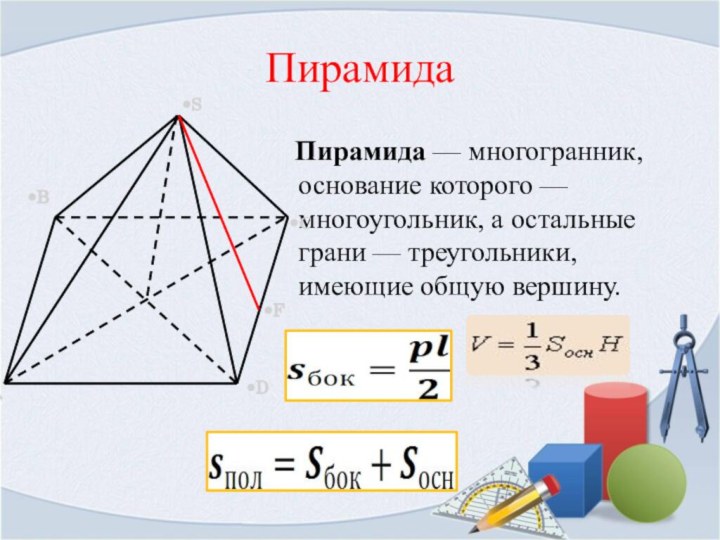
Слайд 9 Пирамида
Пирамида — многогранник, основание которого —многоугольник, а остальные грани — треугольники,

имеющие общую вершину.

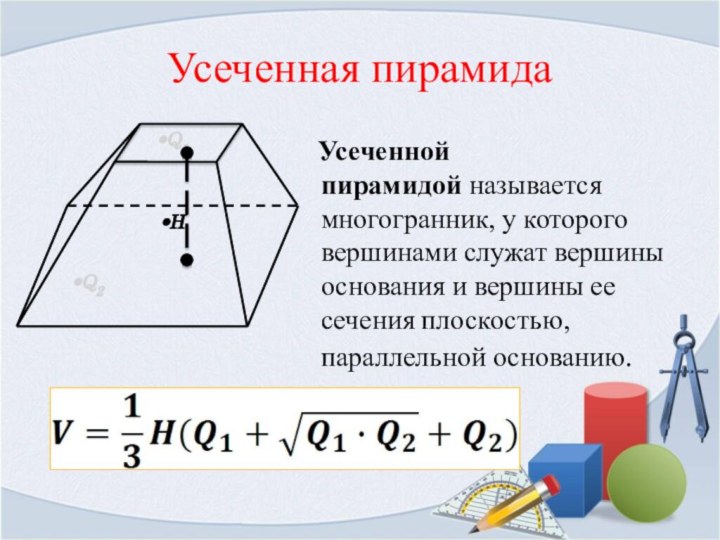
Слайд 10 Усеченная пирамида
Усеченной пирамидой называется многогранник, у

Усеченная пирамида Усеченной пирамидой называется многогранник, у которого вершинами служат вершины

которого вершинами служат вершины основания и вершины ее сечения

плоскостью, параллельной основанию.

Слайд 11 ТЕЛА ВРАЩЕНИЯ Цилиндр
Цилиндр — геометрическое тело, ограниченное цилиндрической

поверхностью и двумя параллельными плоскостями, пересекающими её.
Sосн = R2

Sполн = 2R(R + h)

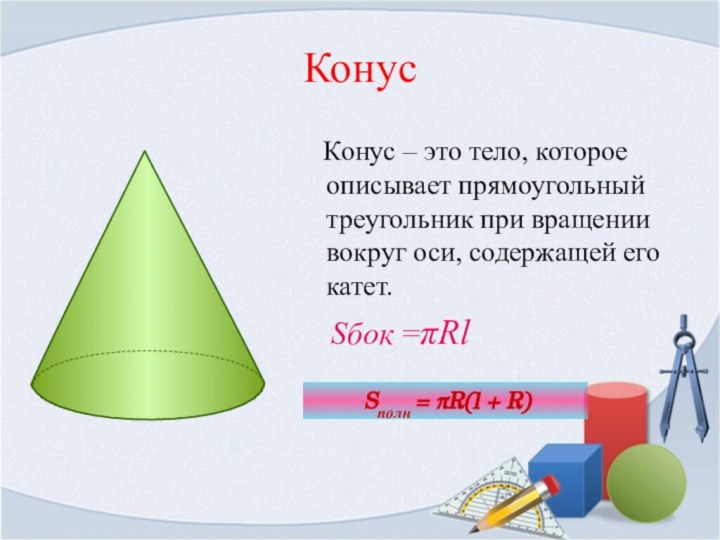
Слайд 12 Конус
Конус – это тело, которое описывает

прямоугольный треугольник при вращении вокруг оси, содержащей его катет.

Sбок =Rl

Sполн = R(l + R)

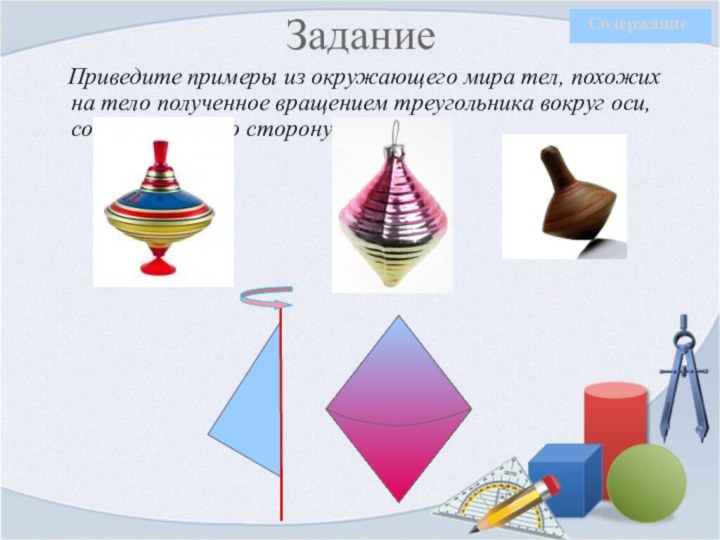
Слайд 13 Задание
Приведите примеры из окружающего мира тел,

похожих на тело полученное вращением треугольника вокруг оси, содержащей

его сторону:

Слайд 14 Шар
Шаром называется тело, которое состоит из всех точек

ШарШаром называется тело, которое состоит из всех точек пространства, находящихся на

пространства, находящихся на расстоянии, не большем данного, от заданной

точки точки.

Сфера – это поверхность все точки которой равноудалены от заданной точки.

V=

Слайд 15 Решение задач (работа в группах)
I группа: №1196 стр

315.
II группа: №1203 стр 1203
III группа: №1216 стр

323

Слайд 16 № 1196. Измерения прямоугольного параллелепипеда равны 8см, 12см

№ 1196. Измерения прямоугольного параллелепипеда равны 8см, 12см и 18см. Найдите

и 18см. Найдите ребро куба, объем которого равен объему

этого параллелепипеда. №1203. Изобразите тетраэдр KLMN и постройте сечение этого тетраэдра плоскостью, проходящей через ребро KL и середину A ребра MN. №1216.Диаметр основания цилиндра равен 1м, высота цилиндра равна длине окружности основания. Найдите площадь боковой поверхности цилиндра.

Слайд 17 Физминутка
Рисуй глазами треугольник
Рисуй глазами треугольник.
Теперь его переверни
Вершиной вниз.
И

ФизминуткаРисуй глазами треугольникРисуй глазами треугольник.Теперь его переверниВершиной вниз.И вновь глазамиты по

вновь глазами
ты по периметру веди.
Рисуй восьмерку вертикально.
Ты головою не

крути,
А лишь глазами осторожно
Ты вдоль по линиям води.
И на бочок ее клади.
Теперь следи горизонтально,
И в центре ты остановись.
Зажмурься крепко, не ленись.
Глаза открываем мы, наконец.
Зарядка окончилась.
Ты – молодец!

Слайд 18 Решите задачу: Классное помещение должно быть таким, чтобы на

Решите задачу: Классное помещение должно быть таким, чтобы на одного учащегося

одного учащегося приходилось не менее 6 м³ воздуха. Можно

ли в кабинете математики , в котором мы находимся, заниматься с 25 учащимися, не нарушая санитарной нормы?

Слайд 19 Когда человеку уютно, приятно, спокойно, он говорит, что

Когда человеку уютно, приятно, спокойно, он говорит, что ему комфортно. Оказывается,

ему комфортно. Оказывается, комфортность определяется формой помещения, его линейными

размерами. Коэффициент комфортности можно найти по формуле: К=36ПV^2: S^3 , где К- коэффициент комфортности, V- объем жилища, S- площадь поверхности жилища, включая пол. И чем меньше коэффициент (в пределах 1), тем комфортнее жилище. Используя формулу, вычислите коэффициент комфортности кабинета математики.