различных головоломок, математических и логических задач. Так как мы
участвуем в математических олимпиадах, то теория графов была особенно актуальна в нашей подготовке. Мы решили разобраться какую роль в обычной жизни играют графы.содержание
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть










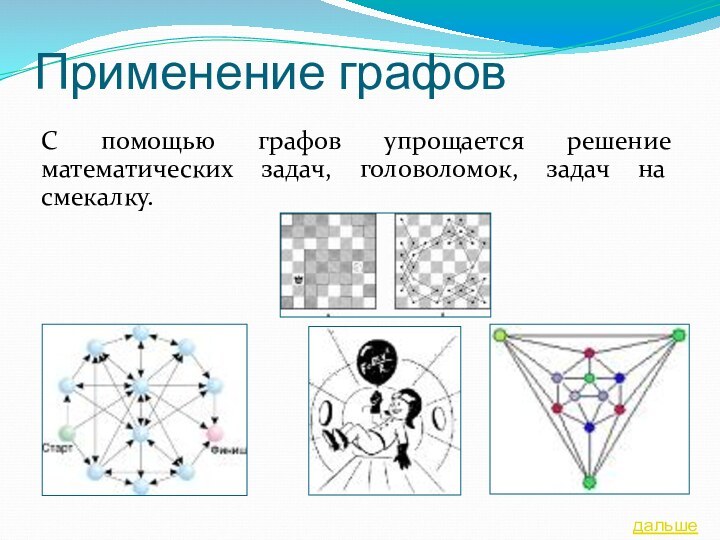
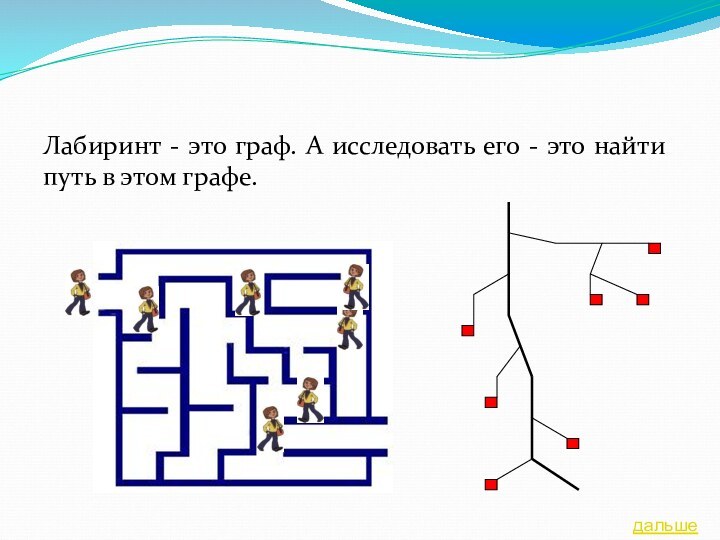

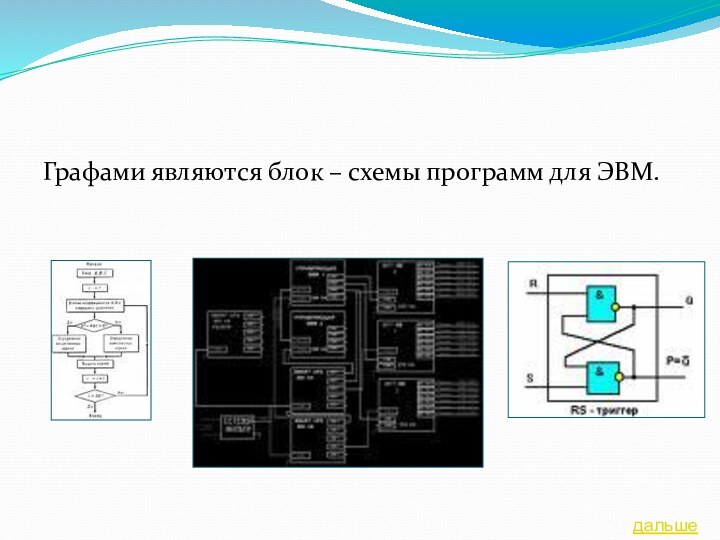






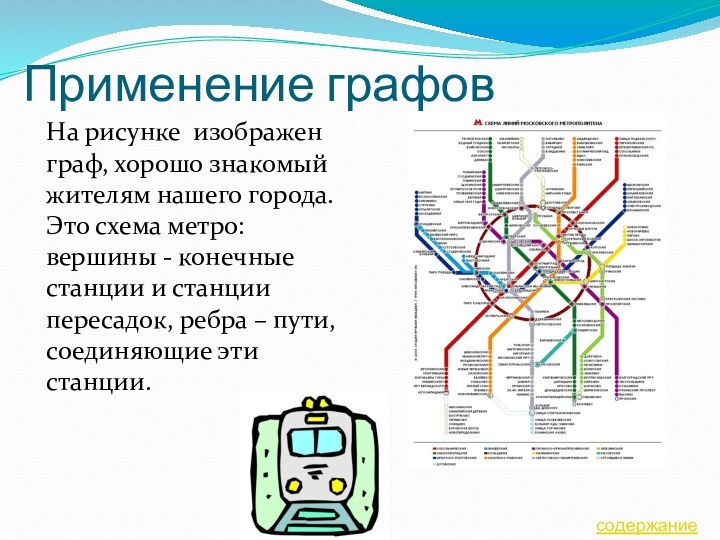






содержание
Дальше
Дальше
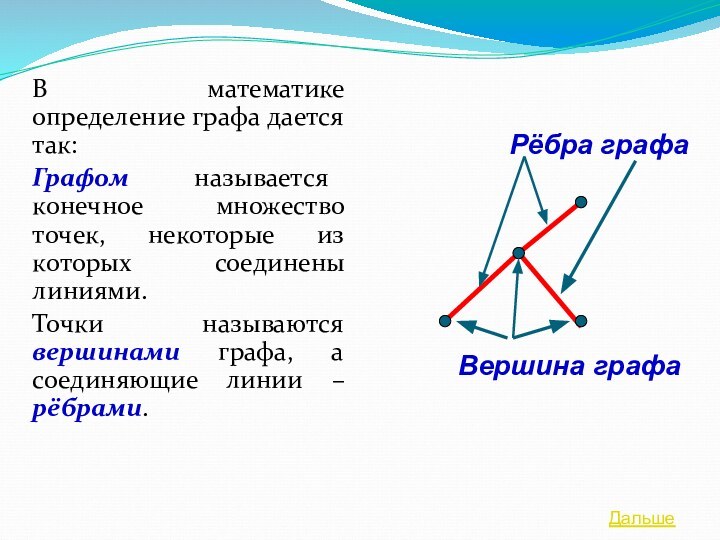
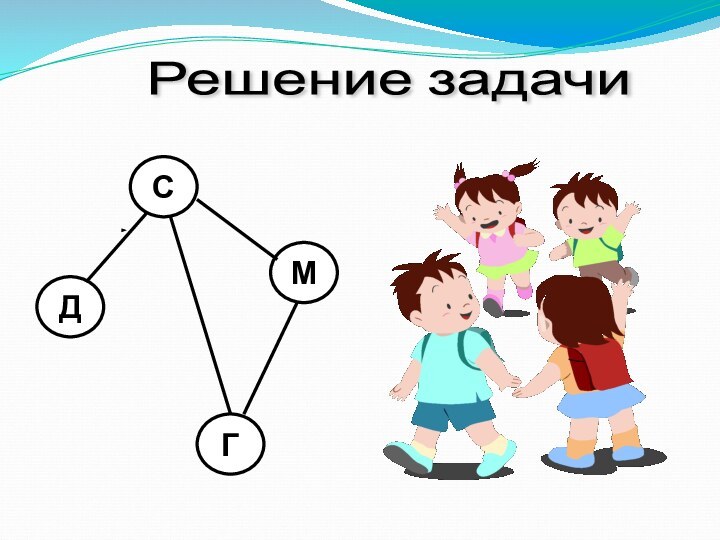
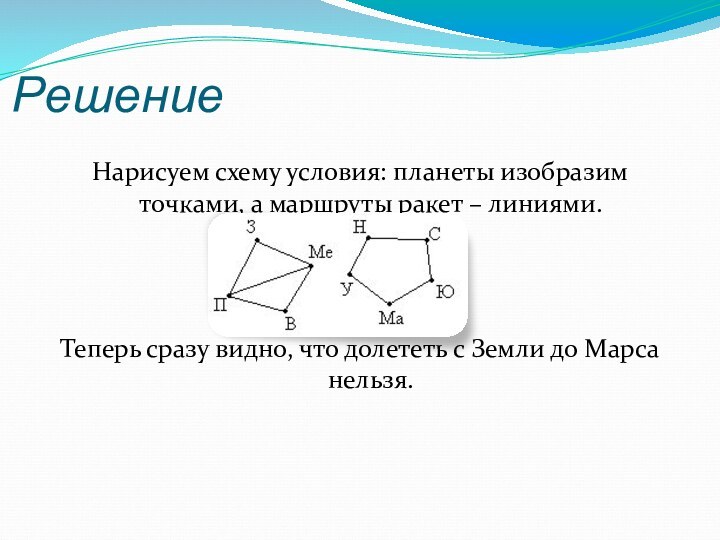
Рёбра графа
Вершина графа
Дальше
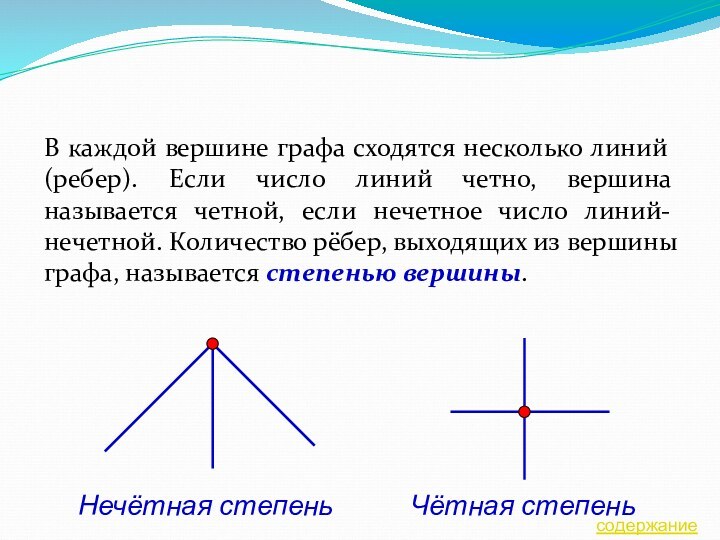
Нечётная степень
Чётная степень
содержание
содержание
Дальше
Дальше
дальше
содержание
дальше
дальше
содержание
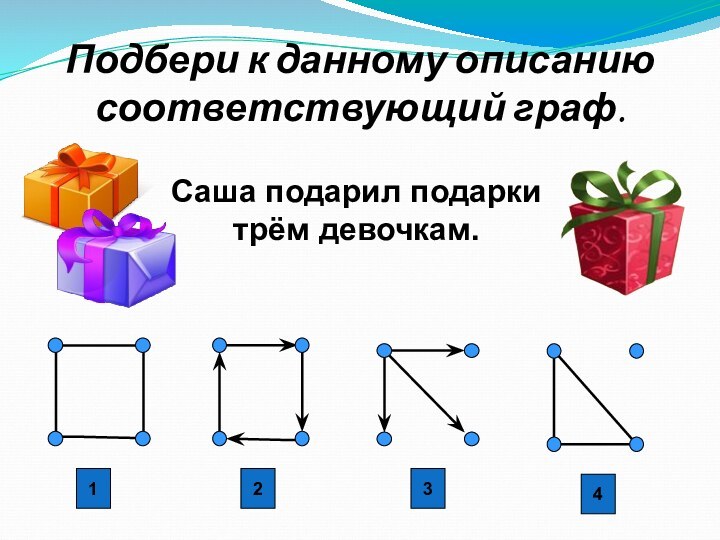
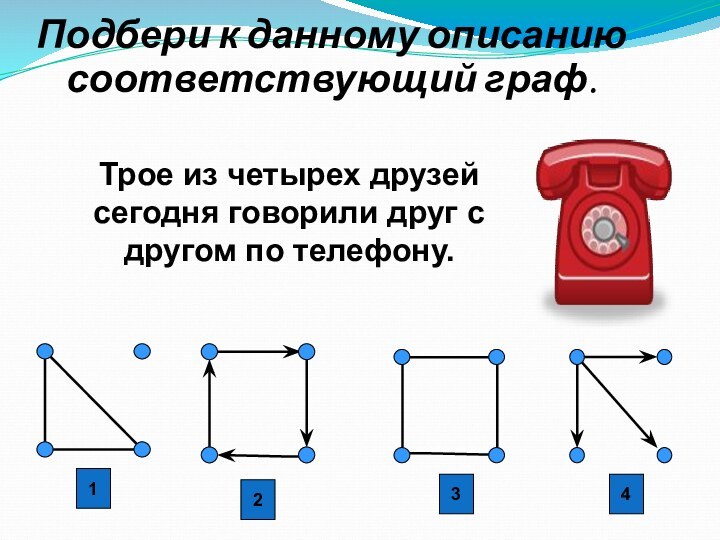
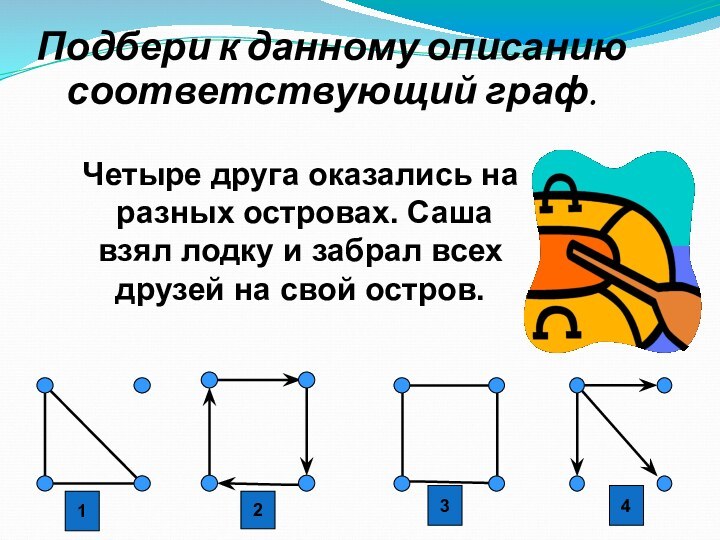
1
2
3
4
2
3
4
1