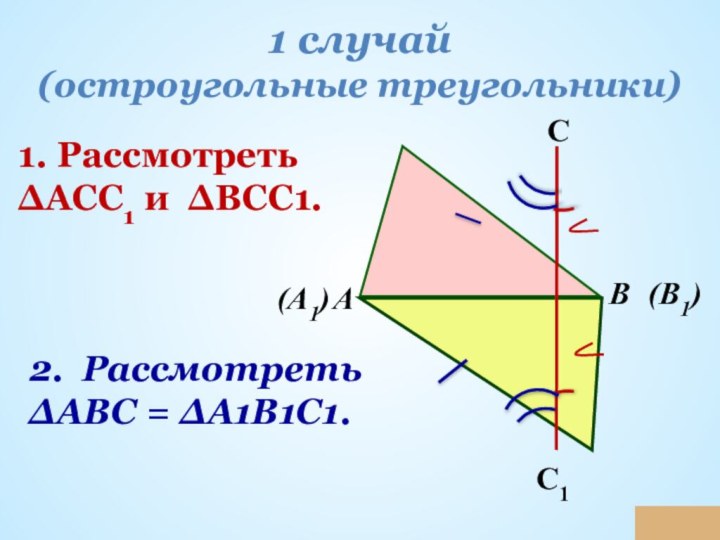
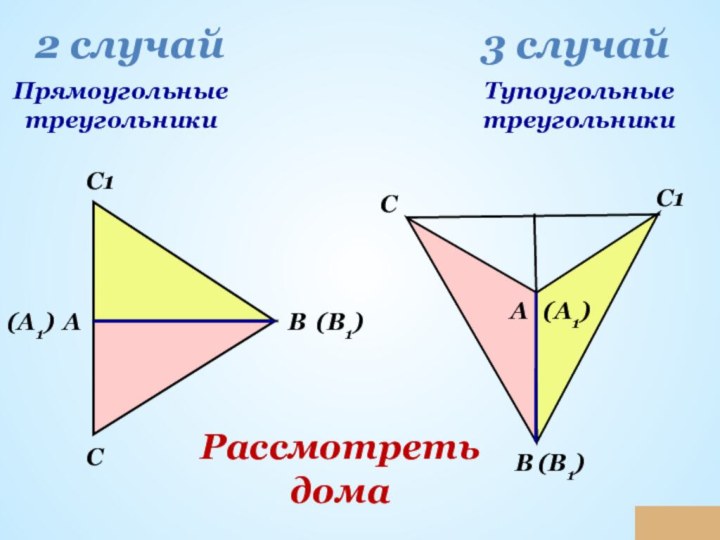
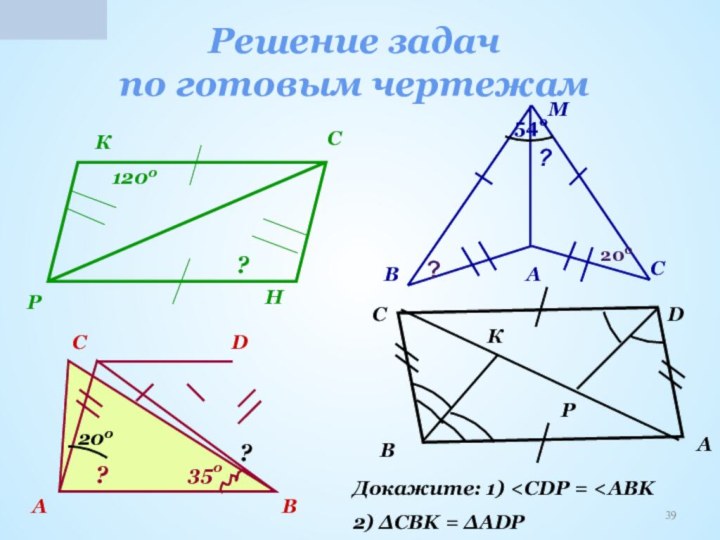
повторение
что такое теорема?
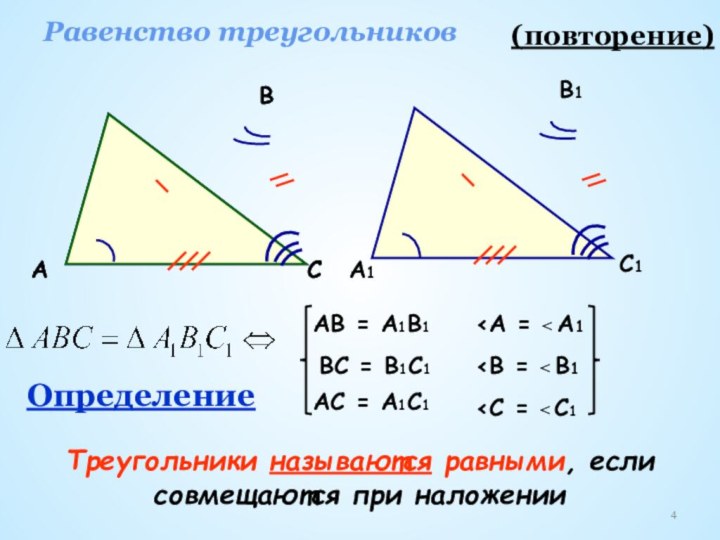
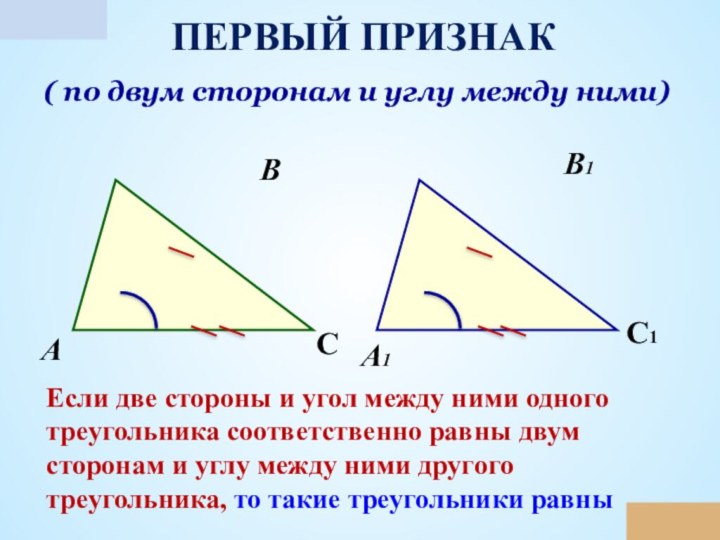
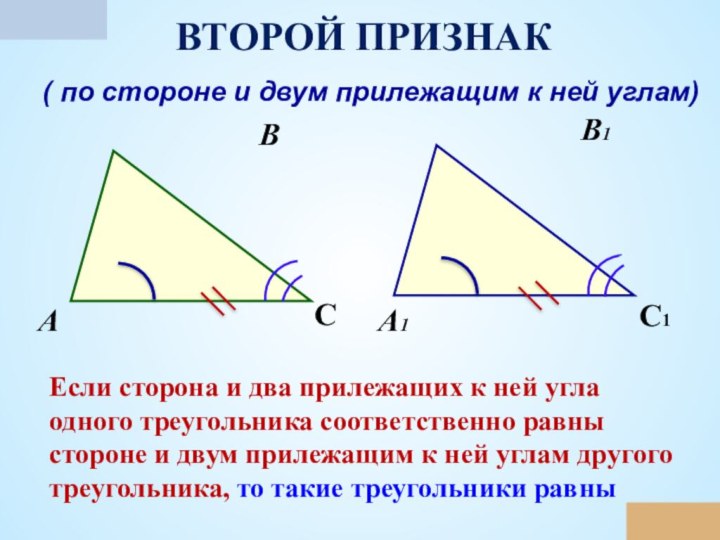
первый признак равенства
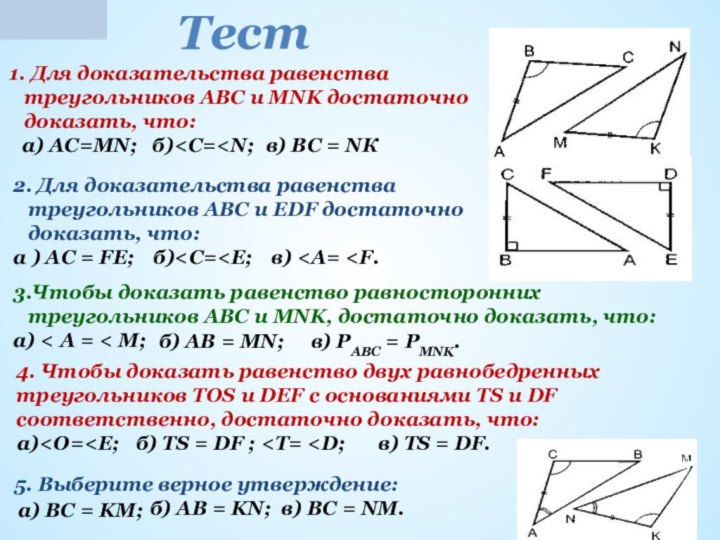
треугольниковзадачи
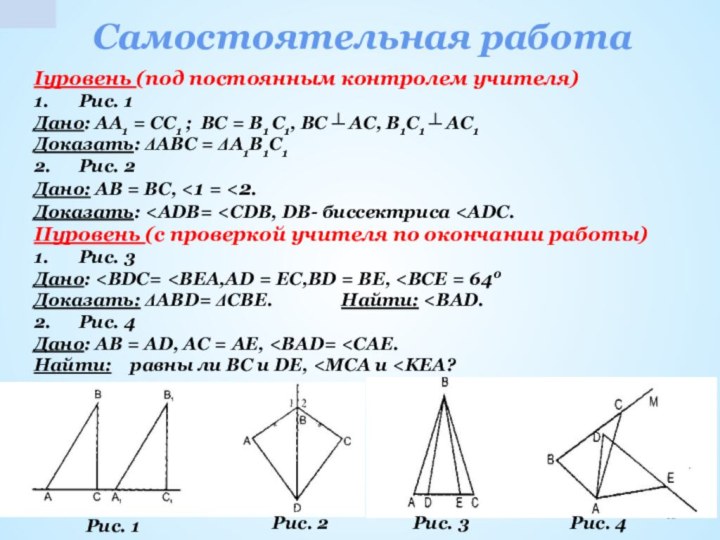
самостоятельная работа (два уровня)
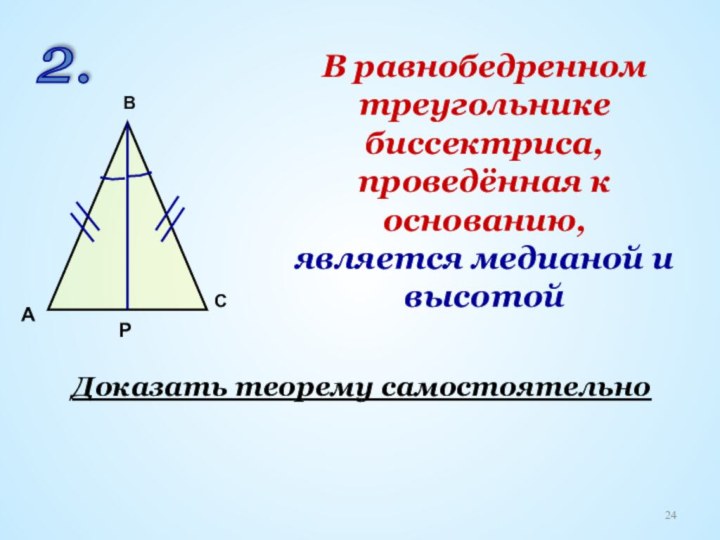
Урок 2: Медиана, биссектриса и высота треугольника
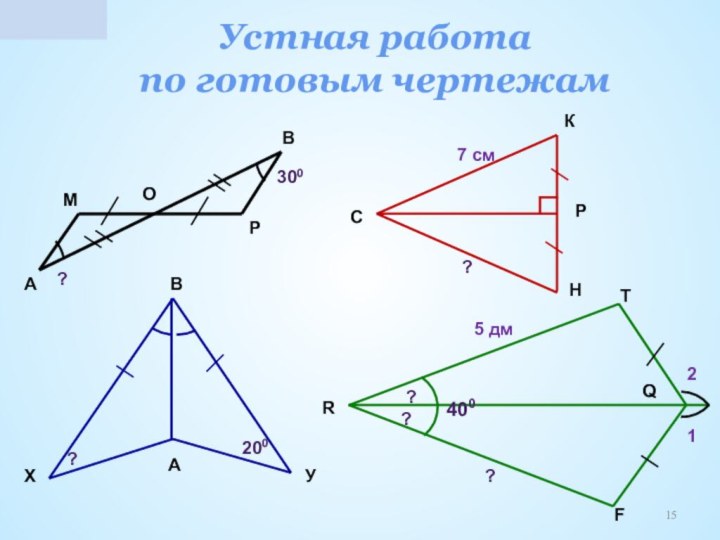
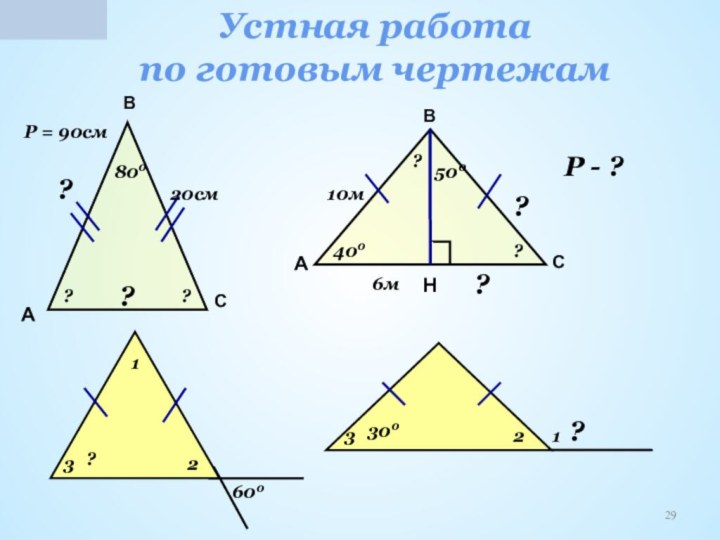
устная работа
перпендикуляр к прямой
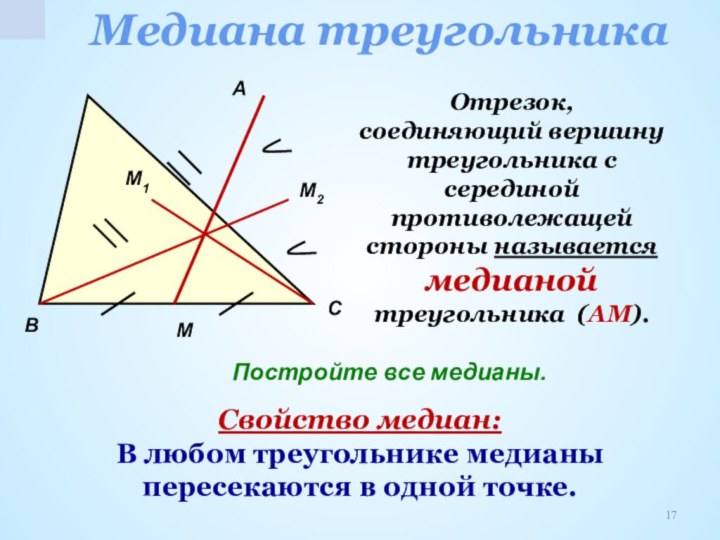
медиана
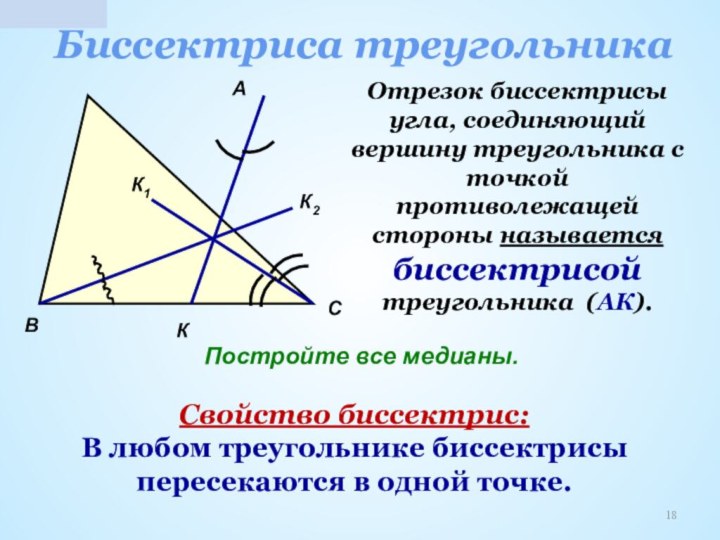
биссектриса
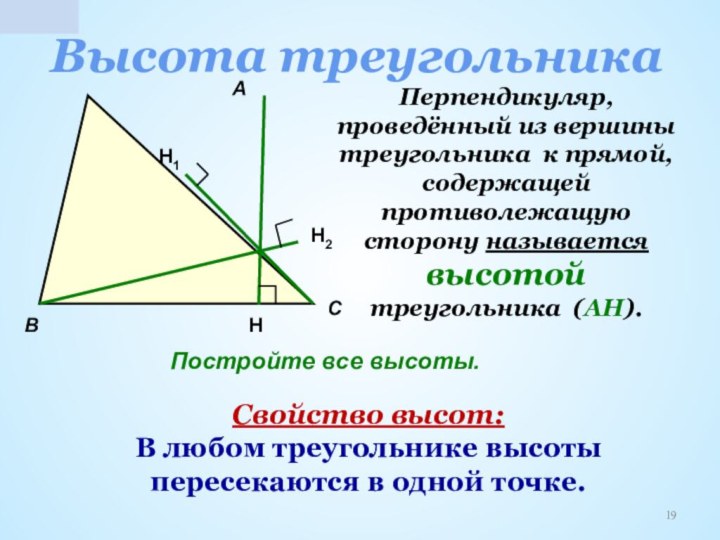
высота
графическая работа