основания перпендикуляра B, отрезок AC называется
наклонной, проведенной из точки
A к прямой a.Точка C называется
основанием наклонной.
Отрезок BC называется
проекцией наклонной.
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть







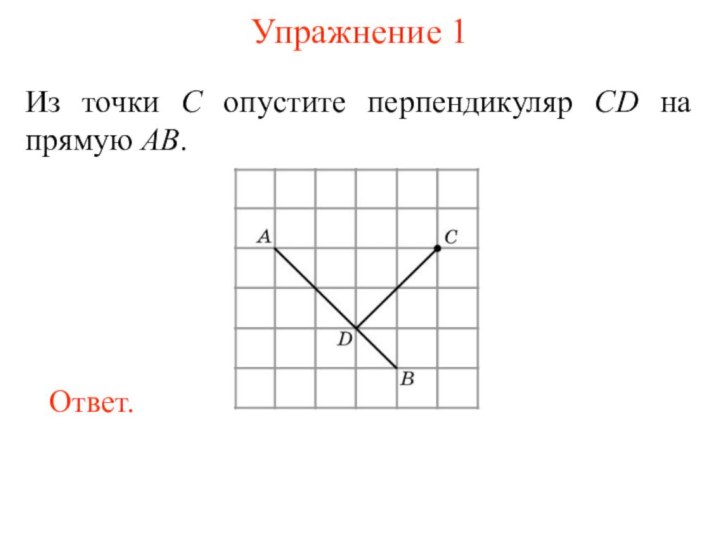
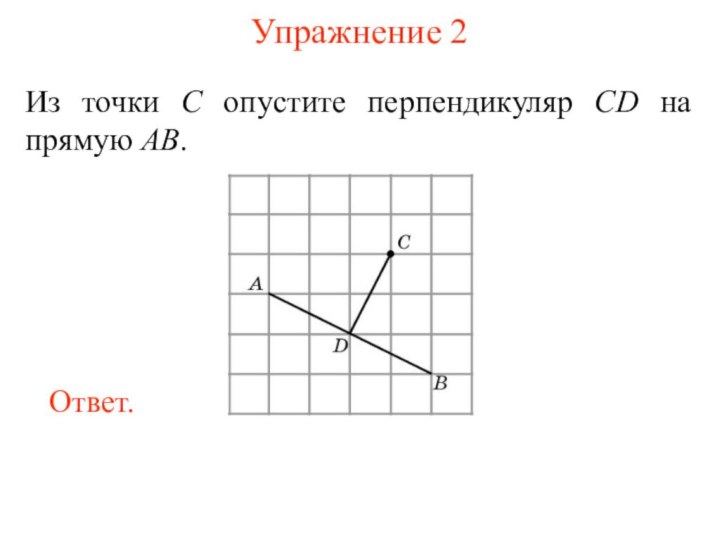
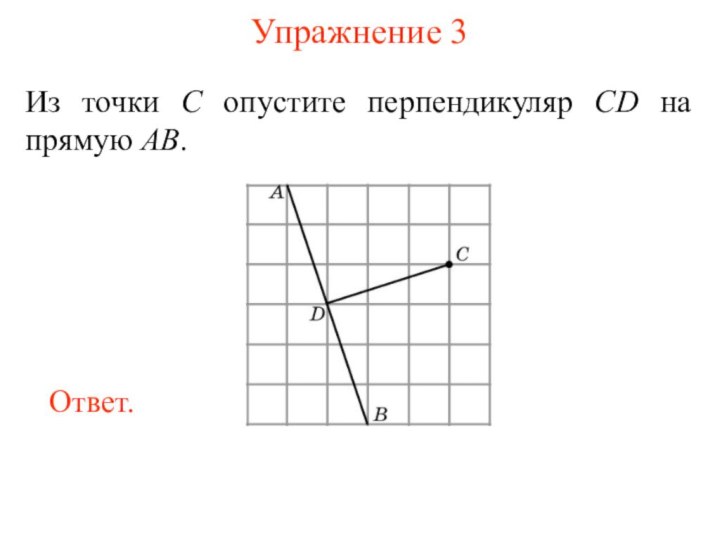












Точка C называется
основанием наклонной.
Отрезок BC называется
проекцией наклонной.
Доказательство. Пусть точка A не принадлежит прямой a, AB – перпендикуляр, AC – наклонная. В прямоугольном треугольнике ABC сторона AB – катет, а AC – гипотенуза. Следовательно, AB < AC.
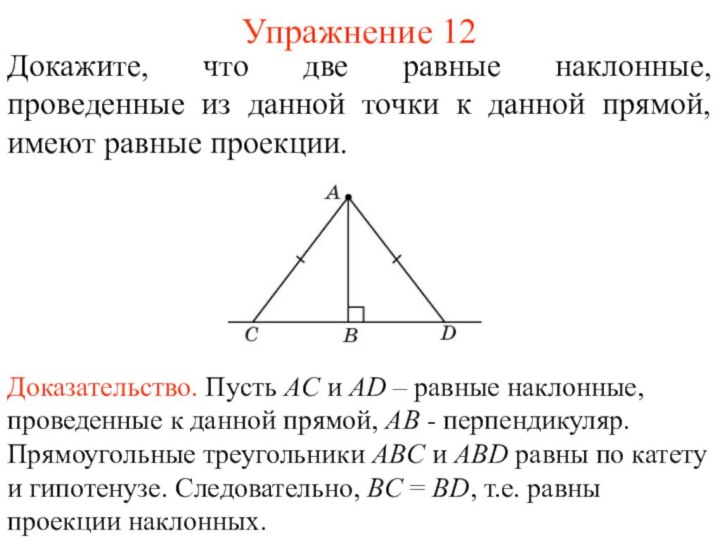
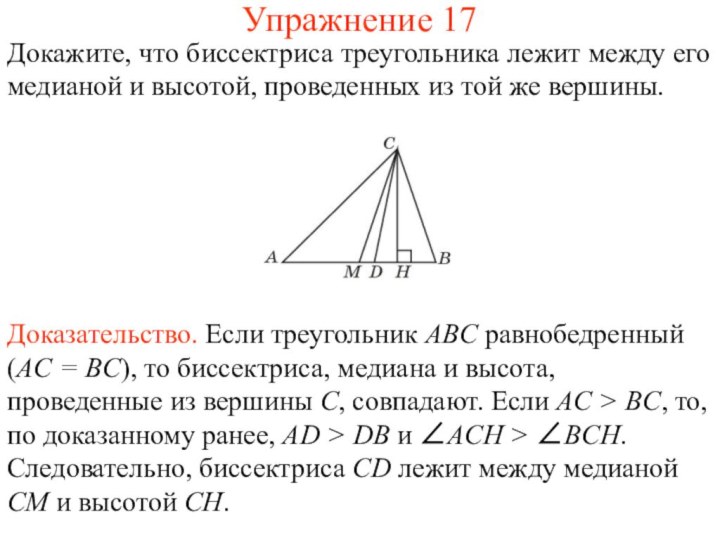
Доказательство. Пусть AC и AD –наклонные, проведенные к данной прямой, AB – перпендикуляр, BD > BC (точки C и D лежат по разные стороны от точки B). Тогда угол ACD – тупой, угол ADC – острый. Так как против большего угла треугольника лежит большая сторона, то AD > AC.
Доказательство. Пусть AC и AD – наклонные, AD > AC, BC, BD – их проекции. Если бы BC было больше BD, то AC было бы больше AD. Если бы BC равнялось AD, то и AC равнялось бы AD. Следовательно, остается единственная возможность AD > AC.
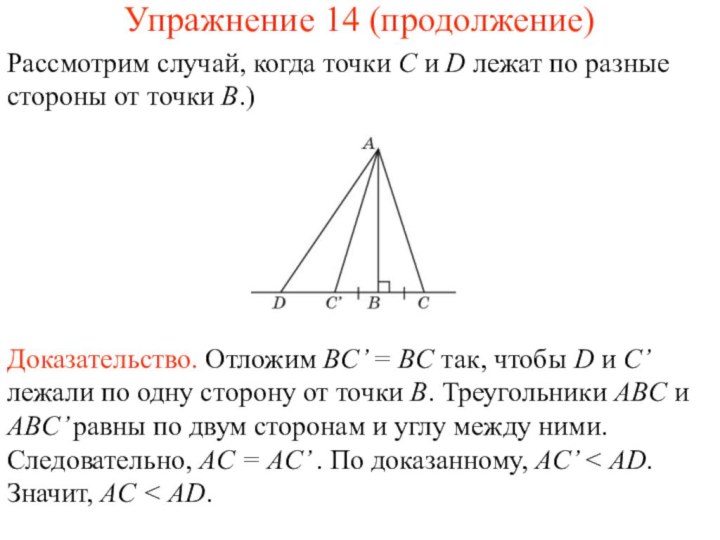
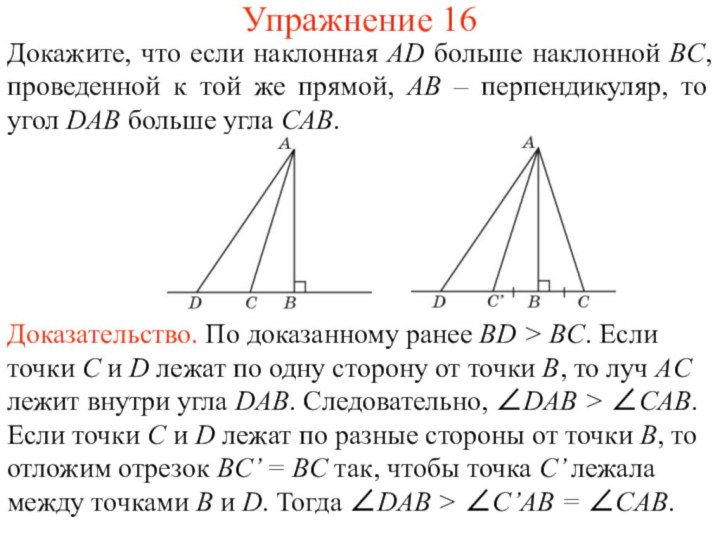
Доказательство. По доказанному ранее BD > BC. Если точки C и D лежат по одну сторону от точки B, то луч AC лежит внутри угла DAB. Следовательно, ∠DAB > ∠CAB. Если точки C и D лежат по разные стороны от точки B, то отложим отрезок BC’ = BC так, чтобы точка C’ лежала между точками B и D. Тогда ∠DAB > ∠C’AB = ∠CAB.