Презентация на тему Основные понятия теории вероятностей

событие?
Из урны наудачу берут один шар. Извлечение шара из

может произойти, называется невозможным.
Пример.
Пусть из урны, содержащей
только черные

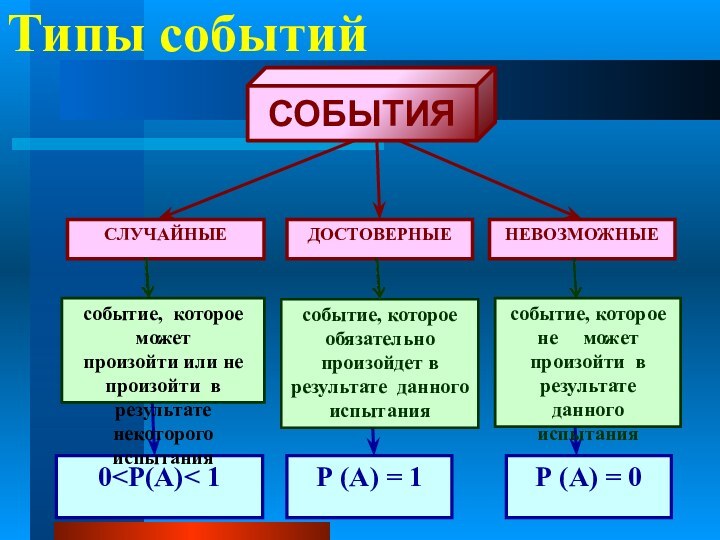
Тогда появление черного шара –
достоверное событие;

Появление белого
шара – невозможное событие.

.
В жизни мы постоянно сталкиваемся с тем, что некоторое

После опубликования результатов
розыгрыша лотереи событие – выигрыш, либо происходит, либо не происходит.

Пример.

утро.
3. Камень падает вниз.
4. Вода становится теплее при нагревании

Распредели события по их типам

СЛУЧАЙНЫЕ

ДОСТОВЕРНЫЕ

НЕВОЗМОЖНЫЕ

одновременно, называются совместными, а те, которые не могут происходить

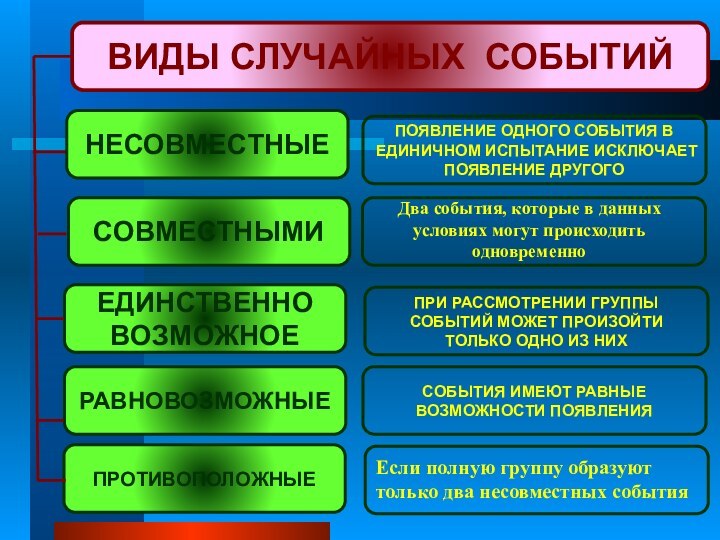
Брошена монета. Появление «герба» исключает появление надписи. События «появился герб» и «появилась надпись» - несовместные.

Пример.

преимуществ.


Пусть бросают игральную кость.
В силу симметрии кубика можно
считать,

Пример.

событий может произойти только одно из них.

Пример.
 

то они называются противоположными.
Пример.
 

ИСПЫТАНИЕ ИСКЛЮЧАЕТ ПОЯВЛЕНИЕ ДРУГОГО
ПРИ РАССМОТРЕНИИ ГРУППЫ СОБЫТИЙ МОЖЕТ ПРОИЗОЙТИ

СОБЫТИЯ ИМЕЮТ РАВНЫЕ ВОЗМОЖНОСТИ ПОЯВЛЕНИЯ

СОВМЕСТНЫМИ

Два события, которые в данных условиях могут происходить одновременно

ПРОТИВОПОЛОЖНЫЕ

Если полную группу образуют только два несовместных события

отношение числа тех исходов, в результате которых наступает событие

Классическое определение вероятности.

взаимоисключающих друг друга вариантов, которым может завершиться случайный эксперимент

времени года
ИСХОДЫ
ОДНОЗНАЧНЫЕ
НЕОДНОЗНАЧНЫЕ
Предполагают несколько различных результатов того или иного

решка, => благоприятный исход = выпала решка. Значит выпадение орла –

Ответ: 5/20=1/4.

ИСХОДЫ
Вероятность
каждого
исхода

(события,
которое соответствует единственному исходу из N
равновозможных)

, оно и будет равно вероятности

Значит

Алгоритм нахождения вероятности
случайного события.

Для нахождения вероятности случайного события А при проведении некоторого испытания следует найти:

1) число N всех возможных исходов данного испытания;

2) количество N(A) тех исходов, в которых наступает событие А;

Принято вероятность события А обозначать так: Р(А).

завод привезли партию из 1000 подшипников. Случайно в эту

Благоприятное событие А: подшипник окажется стандартным.

Решение.

Количество всех возможных исходов
N = 1000.

Количество благоприятных исходов N(A)=1000-30=970.

Значит:

Ответ: 0.97.

А: герб выпадет хотя бы один раз.
Кол-во всех возможных

Кол-во благоприятных исходов N(A)={ГГ, ГР, РГ} = 3.

Значит:

Ответ: 0.75.

событий А и В называют событие А*В, состоящее в

Если события А и В независимы (они происходят в разных испытаниях, и исход одного испытания не может влиять на исход другого), то вероятность того, что наступят оба этих события, равна Р(А)*Р(В):
Р(А*В)=Р(А)*Р(В)
Например, вероятность выпадения двух шестерок при двукратном бросании кубика равна: 1/6*1/6=1/36.

костей суммарное число очков окажется равным 5.
Благоприятное событие А:

Количество всех возможных исходов:

Кол-во благоприятных исходов N(A)=

1-я кость - 6 вариантов
2-я кость - 6 вариантов

N=6∙6=36.

{1 + 4, 2 + 3, 3 + 2, 4 + 1}=4

Решение:

Значит:

Ответ:

суммы событий
.

Для произвольных событий А и В вероятность суммы этих событий равна сумме их вероятностей без вероятности их совместного события:

равна 1:

3 очка, либо 4 очка.

0, 01. А вероятность того, что он в этот

суммы двух совместных событий равна сумме вероятностей этих событий,

шаров. Наудачу вынимают 8 шаров. Определите вероятность события А

Решение: Р(А) = 0, т.к. это событие А - невозможное.
Ответ: 0.

докладов: в первый день – 30 докладов, а остальные

Решение:

Благоприятное событие А: доклад профессора М. окажется запланированным на последний день конференции.

Кол-во всех возможных исходов N = 50.

Кол-во благоприятных исходов N(A)=(50-30):2=10.

Значит:

Ответ: 0.2.

на игровые пары случайным образом с помощью жребия. Всего

Решение:

Благоприятное событие А: в первом туре Ярослав Исаков будет играть с каким – либо теннисистом
из России

Кол-во всех возможных исходов N = 45.

Кол-во благоприятных исходов N(A)=18.

Значит:

Ответ: 0.4.

среднем из 180  сумок восемь сумок со скрытыми дефектами.

Решение:

N(A) = 180-8 = 172 сумки качественные,
N = 180 всего сумок

P(A) = 172/180 = 0,955...≈ 0,96

Ответ: 0,96.

В таблице приведены результаты диагностической работы по

Решение:
7+20+15+8 = 50 – всего учащихся
(2*7+3*20+4*15+5*8):50 = 3,48 ≈ 3 – среднее по школе значение оценки.
15+8=23 – количество девятиклассников, получивших оценку выше средней по школе. Р = 23/50 = 0,46.
Ответ: 0,46.

пароля для входа на сайт, но помнит, что они

Решение:
Подсчитаем количество всех возможных двузначных чисел с разными цифрами, меньшее 30, которые может набрать абонент:

Таких чисел 18. Так как только одно число правильное, то искомая вероятность Р=1/18. Ответ: 1/18.

выучить один из тех 25 билетов, которые будут предложены

Задача

Решение:

N = 25 – количество билетов
N(A) = 25-1 = 24 – количество выученных билетов
P(A)= 24/25 = 0,96 – искомая вероятность.
Ответ: 0,96.

белый. Вытаскивая кубики наугад, мы ставим их последовательно друг

Сколько всего возможно результатов опыта?
Пусть Ч – черный кубик, К – красный кубик, Б – белый кубик, тогда

ЧКБ, ЧБК, БЧК, БКЧ, КЧБ, КБЧ.

Решение:

n=6

Ответ: