Презентация на тему Правильные многогранники и их свойства

на основе определения многогранников).

Рассмотреть свойства правильных многогранников.

Познакомить с

историческими фактами, связанными с теорией правильных многогранников.

Развивать познавательный интерес учащихся, учить их видеть связь между математикой и окружающей жизнью;

самых увлекательных глав геометрии.

Л. А. Люстерник

ограниченное со всех сторон плоскими многоугольниками, называемыми гранями.
Концы

ребер - вершинами

д.

одну сторону от плоскости каждой из его граней.

которого все грани являются правильными многоугольниками, и все многогранные

углы при вершинах равны.

Приведён пример правильного многогранника (икосаэдр), его гранями являются правильные (равносторонние) треугольники.

многогранника должно сходиться столько правильных n – угольников, чтобы

сумма их углов была меньше 3600. Т.е должна выполняться формула βk < 3600 ( β-градусная мера угла многоугольника, являющегося гранью многогранника, k – число многоугольников, сходящихся в одной вершине многогранника.)

В любом выпуклом многограннике сумма числа граней и числа вершин больше числа ребер на 2.

у которого грани правильные треугольники и в каждой вершине

сходится по три ребра и по три грани. У тетраэдра: 4 грани, четыре вершины и 6 ребер.

Тетраэдр

у которого грани- правильные треугольники и в каждой вершине

сходится по четыре ребра и по четыре грани. У октаэдра: 8 граней, 6 вершин и 12 ребер

Октаэдр

которого грани – квадраты и в каждой вершине сходится

по три ребра и три грани. У него: 6 граней, 8 вершин и 12 ребер.

Куб (гескаэдр)

которого грани – треугольники и в каждой вершине сходится

по пять ребер и пять граней. У него: 12 граней, 12 вершин и 22 ребер.

Икосаэдр

в каждой вершине сходится по три ребра и три

грани. У додекаэдра:12 граней, 20 вершин и 30 ребер.

многогранников были известны в Древней Греции – именно им

посвящена завершающая, XIII книга «Начал» Евклида.

Немного истории

занимали видное место в идеалистической картине мира древнегреческого философа

Платона.

Додекаэдр символизировал всё мироздание, почитался главнейшим. Уже по латыни в средние века его стали называть «пятая сущность» или guinta essentia, «квинта эссенциа», отсюда происходит вполне современное слово «квинтэссенция», означающее всё самое главное, основное, истинную сущность чего-либо.

полуправильные выпуклые многогранники, или Архимедовы тела. У них все

многогранные углы равны, все грани - правильные многоугольники, но нескольких различных типов.

не только почувствовать их красоту, но и обнаружить некоторые

закономерности, возможно, имеющие прикладное значение.

Некоторые из правильных и полуправильных тел встречаются в природе в виде кристаллов, другие — в виде вирусов, простейших микроорганизмов.

Кристаллы — тела, имеющие многогранную форму. Вот один из примеров таких тел: кристалл пирита (сернистый колчедан FeS) — природная модель додекаэдра. Пирит (от греч. “пир” — огонь) — сернистое железо или серный колчедан, наиболее распространенный минерал из группы сульфидов. Размеры кристаллов пирита часто достигают нескольких сантиметров и являются хорошим коллекционным материалом. От других подобных ему минералов отличается твердостью: царапает стекло.

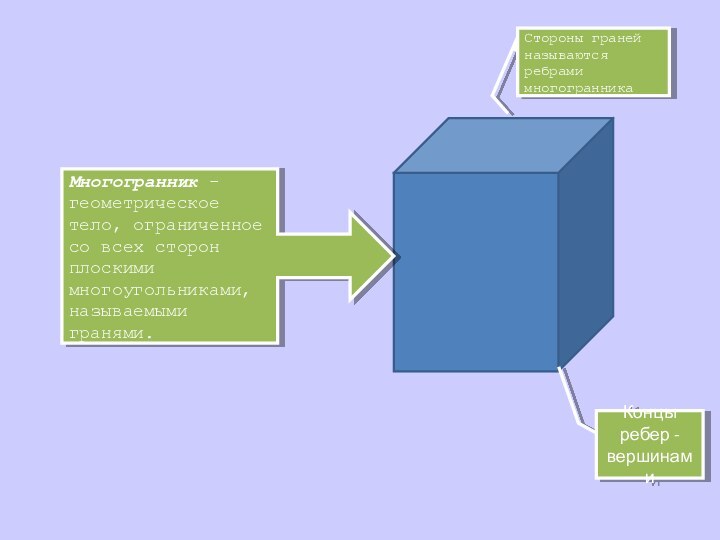
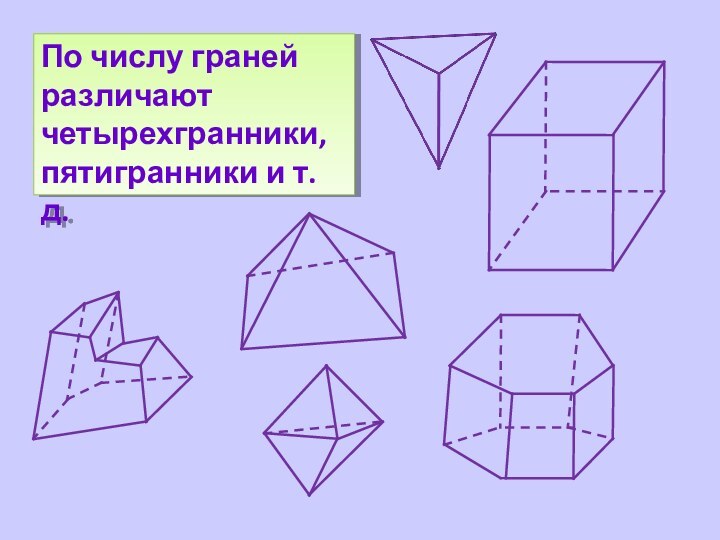
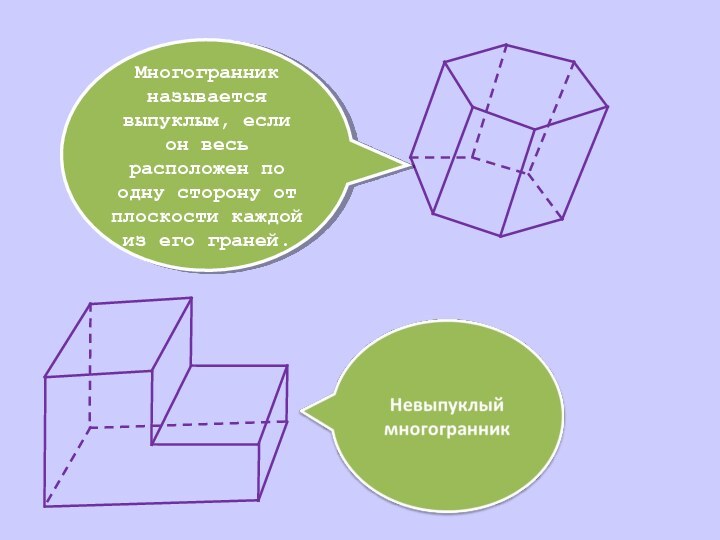
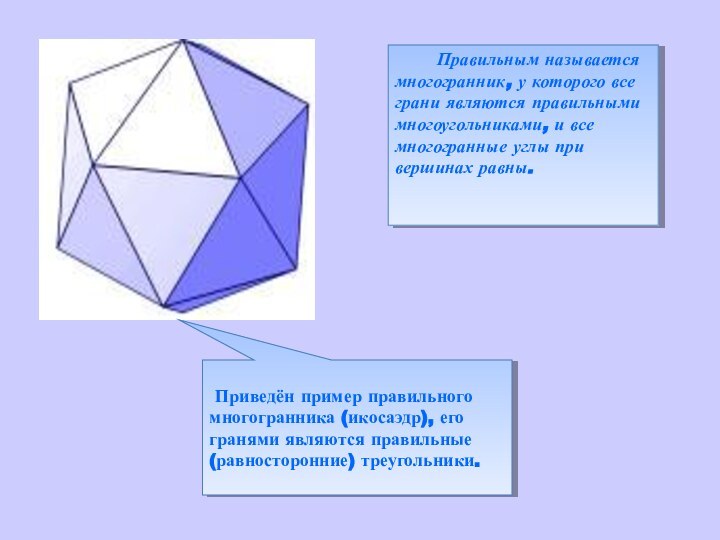
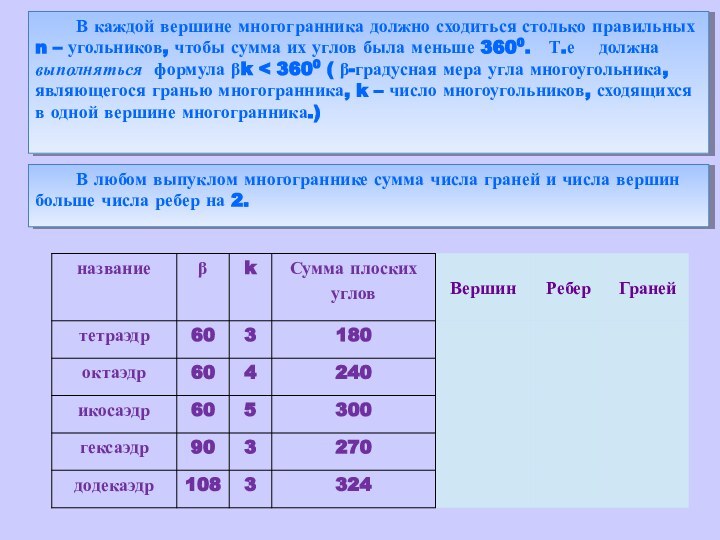
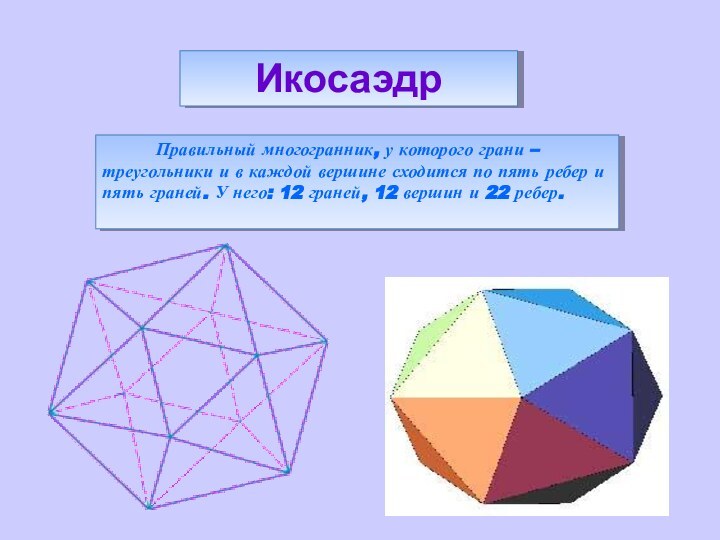
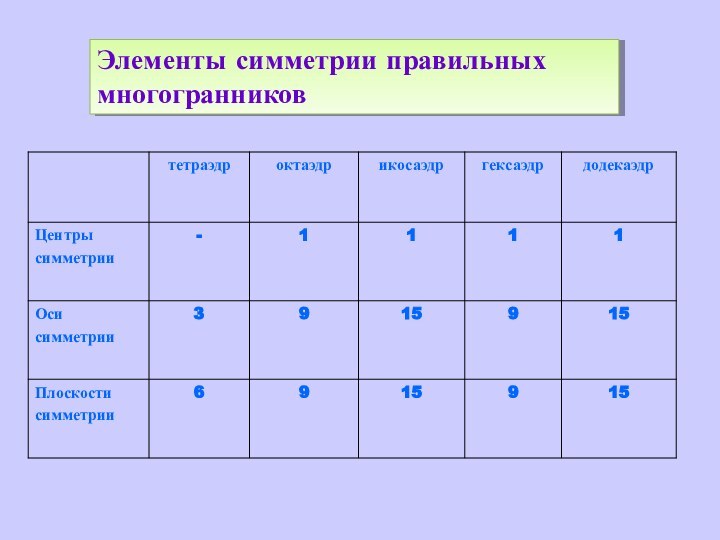
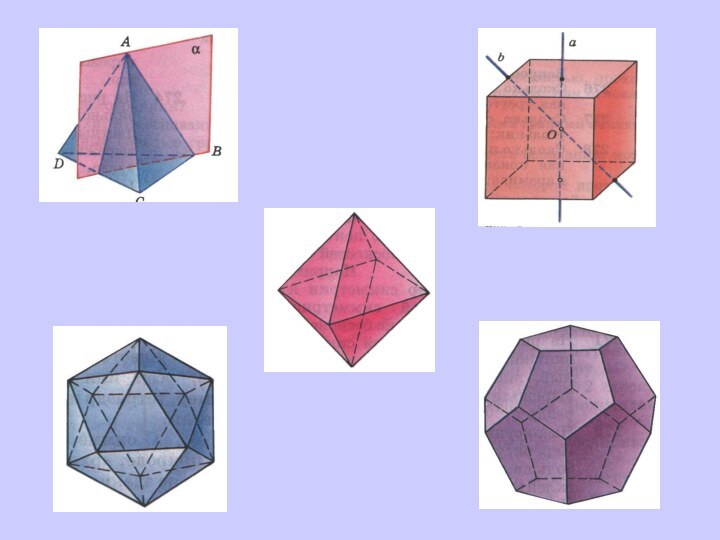
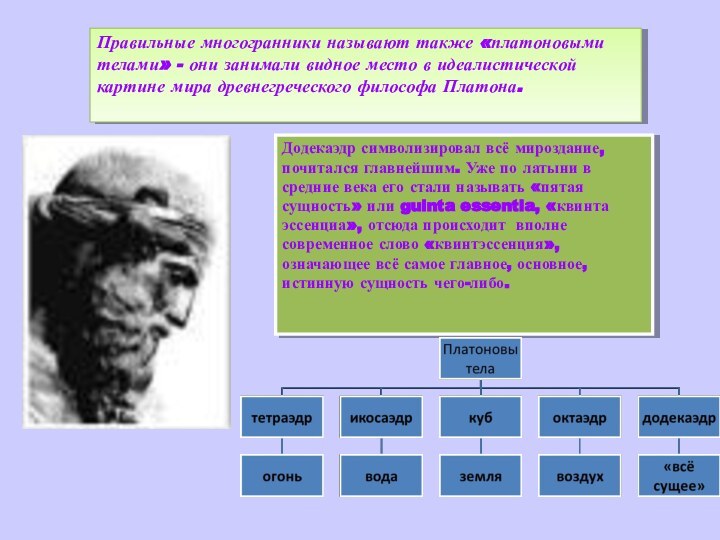
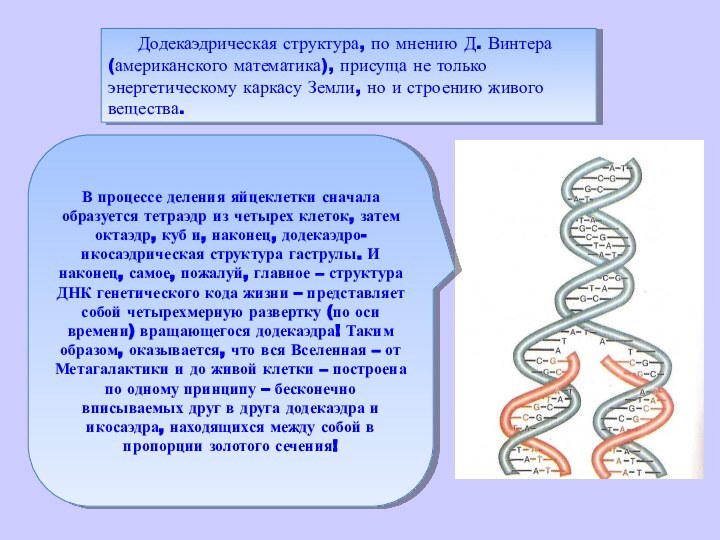
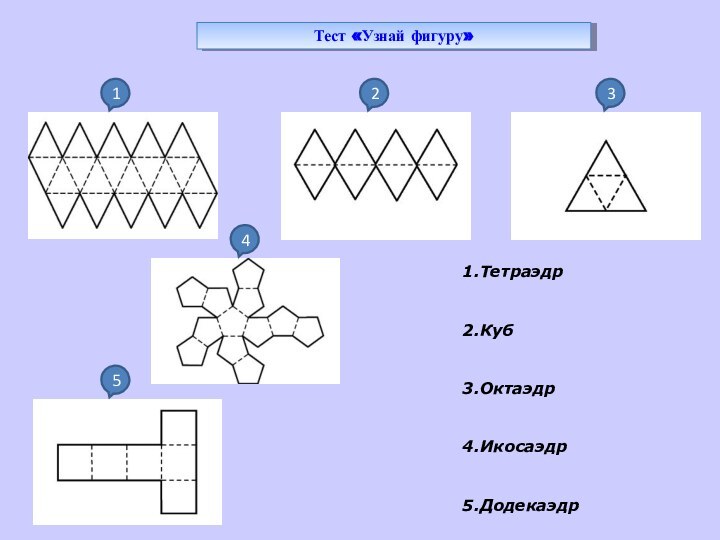
объемных фигур. Существует много данных о сравнении структур и

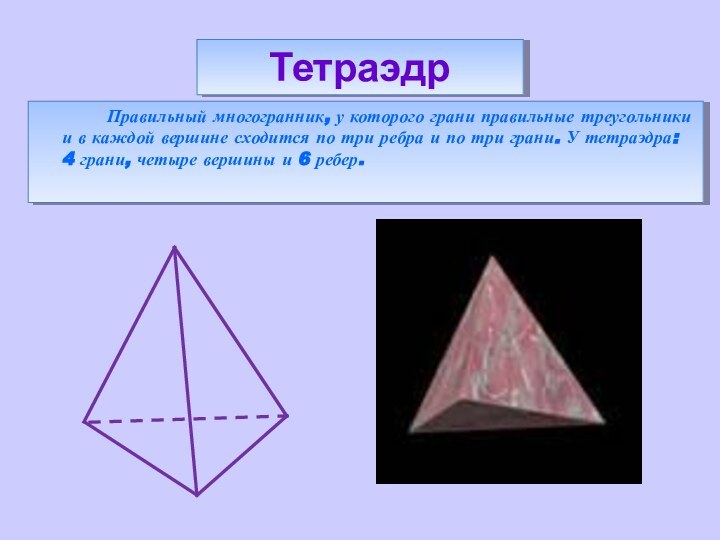
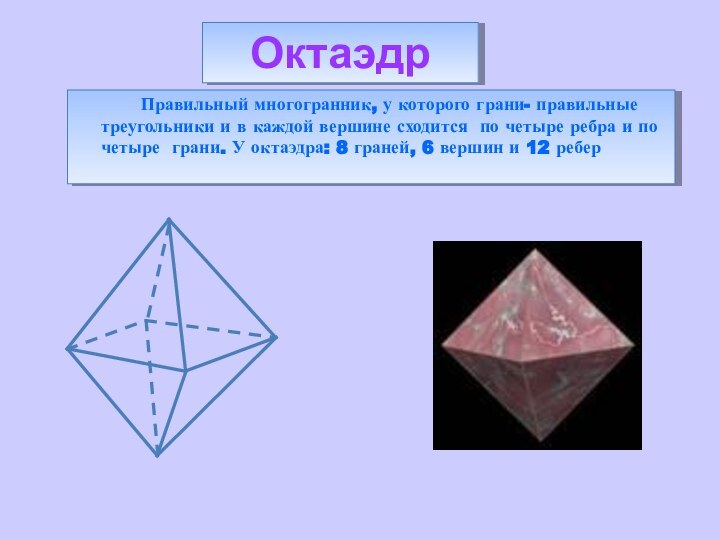
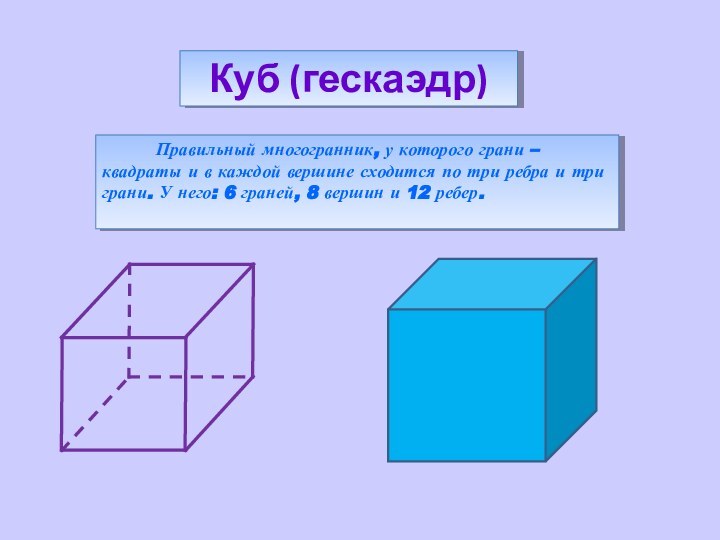
процессов Земли с вышеуказанными фигурами. Полагают, что четырем геологическим эрам Земли соответствуют четыре силовых каркаса правильных Платоновских тел: Протозою - тетраэдр (четыре плиты), Палеозою - гексаэдр (шесть плит) ,Мезозою - октаэдр (восемь плит) ,Кайнозою - додекаэдр (двенадцать плит).

Существует гипотеза, по которой ядро Земли имеет форму и свойства растущего кристалла, оказывающего воздействие на развитие всех природных процессов, идущих на планете. «Лучи» этого кристалла, а точнее его силовое поле, обусловливают икосаэдро-додекаэдрическую структуру Земли, проявляющуюся в том, что в земной коре как бы проступают проекции вписанных в земной шар правильных многогранников: икосаэдра и додекаэдра. 62 их вершины и середины ребер, называемые узлами, оказывается, обладают рядом специфичecких свойств, позволяющих объяснить многие непонятные явления.

примечательных культур и цивилизаций Древнего мира, можно заметить закономерность

в их расположении относительно географических полюсов и экватора планеты. Многие залежи полезных ископаемых тянутся вдоль икосаэдрово-додекаэдровой сетки. Еще более удивительные вещи происходят в местах пересечения этих ребер: тут располагаются очаги древнейших культур и цивилизаций: Перу, Северная Монголия, Гаити, Обская культура и другие. В этих точках наблюдаются максимумы и минимумы атмосферного давления, гигантские завихрения Мирового океана, здесь шотландское озеро Лох-Несс, Бермудский треугольник. Дальнейшие исследования Земли, возможно, определят отношение к этой красивой научной гипотезе, в которой, как видно, правильные многогранники занимают важное место.

присуща не только энергетическому каркасу Земли, но и строению

живого вещества.

В процессе деления яйцеклетки сначала образуется тетраэдр из четырех клеток, затем октаэдр, куб и, наконец, додекаэдро-икосаэдрическая структура гаструлы. И наконец, самое, пожалуй, главное – структура ДНК генетического кода жизни – представляет собой четырехмерную развертку (по оси времени) вращающегося додекаэдра! Таким образом, оказывается, что вся Вселенная – от Метагалактики и до живой клетки – построена по одному принципу – бесконечно вписываемых друг в друга додекаэдра и икосаэдра, находящихся между собой в пропорции золотого сечения!

исследований. Их формы - завершенные и причудливые, широко используются

в декоративном искусстве.

являются, конечно, графические фантазии Маурица Корнилиса Эшера (1898-1972), голландского

художника, родившегося в Леувардене.

Мауриц Эшер в своих рисунках как бы открыл и интуитивно проиллюстрировал законы сочетания элементов симметрии, т.е. те законы, которые властвуют над кристаллами, определяя и их внешнюю форму, и их атомную структуру, и их физические свойства.

Математик, так же как и художник или поэт, создает узоры, и если
его узоры более устойчивы, то лишь потому, что они составлены из идей.

из четырех правильных многоугольников:
А) Тетраэдр

В) Куб С) Октаэдр D) Икосаэдр Е) Додекаэдр

2. Многогранник, составленный из пятиугольников:
А) Тетраэдр В) Куб С) Октаэдр D) Икосаэдр Е) Додекаэдр

3. Многогранник, составленный из восьми треугольников:
А) Тетраэдр В) Куб С) Октаэдр D) Икосаэдр Е) Додекаэдр

4. Многогранник, каждая вершина которого является вершиной пяти треугольников:
А) Тетраэдр В) Куб С) Октаэдр D) Икосаэдр Е) Додекаэдр

5. Многогранник, каждая вершина которого является вершиной трех квадратов:
А) Тетраэдр В) Куб С) Октаэдр D) Икосаэдр Е) Додекаэдр

6. Многогранник с восьмью гранями:
А) Тетраэдр В) Куб С) Октаэдр D) Икосаэдр Е) Додекаэдр
 
7. Многогранник, с четырьмя гранями:
А) Тетраэдр В) Куб С) Октаэдр D) Икосаэдр Е) Додекаэд
 
 

А) Тетраэдр В)

Куб С) Октаэдр D) Икосаэдр Е) Додекаэдр
 
9. Многогранник, у которого 30 ребер:
А) Тетраэдр В) Куб С) Октаэдр D) Икосаэдр Е) Додекаэдр
 
10. Многогранник, у которого 8 вершин:
А) Тетраэдр В) Куб С) Октаэдр D) Икосаэдр Е) Додекаэдр
 
11. Многогранник, не имеющий центра симметрии:
А) Тетраэдр В) Куб С) Октаэдр D) Икосаэдр Е) Додекаэдр
 
12. Многогранник, имеющий 9 осей и плоскостей симметрии:
А) Тетраэдр В) Куб С) Октаэдр D) Икосаэдр Е) Додекаэдр
 
13. Многогранник, имеющий 15 осей и плоскостей симметрии:
А) Тетраэдр В) Куб С) Октаэдр D) Икосаэдр Е) Додекаэдр
 
14. Многогранник, у которого 3 оси симметрии:
А) Тетраэдр В) Куб С) Октаэдр D) Икосаэдр Е) Додекаэдр
 
15. Многогранник, имеющий 6 плоскостей симметрии:
А) Тетраэдр В) Куб С) Октаэдр D) Икосаэдр Е) Додекаэдр