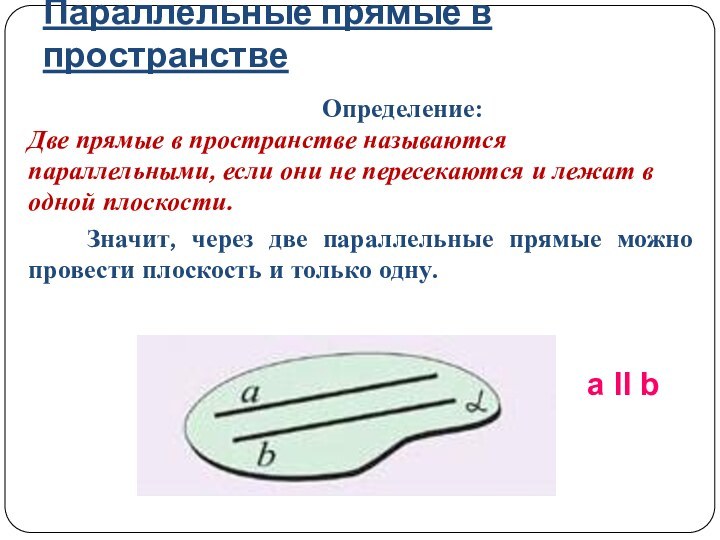
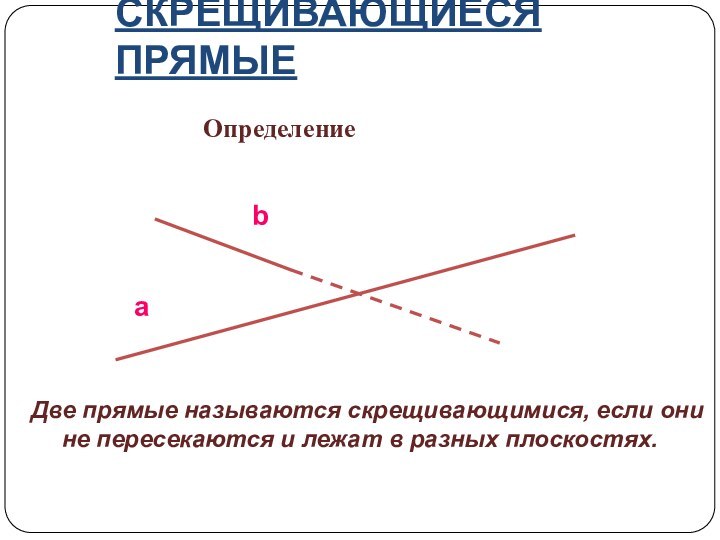
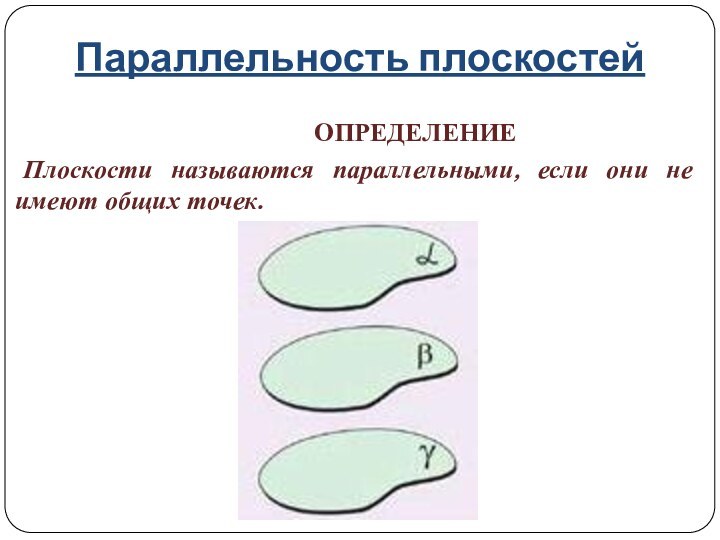
Определение: Две прямые в пространстве называются параллельными, если они не пересекаются и лежат в одной плоскости.
Значит, через две параллельные прямые можно провести плоскость и только одну.
a ΙΙ b
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть


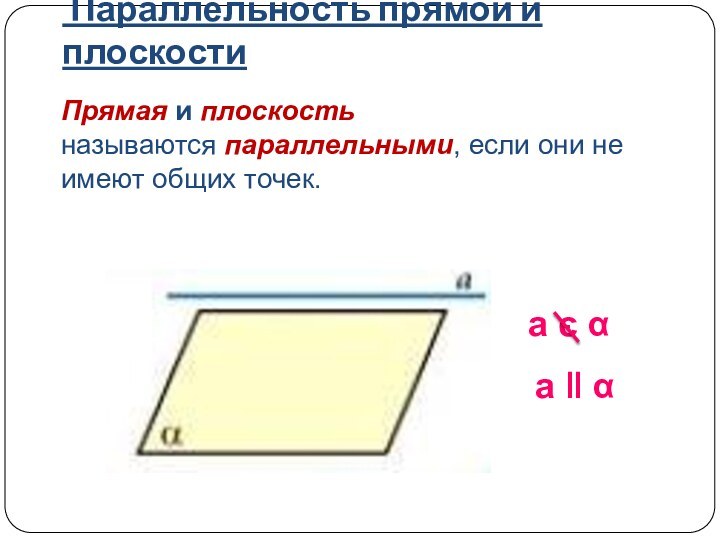
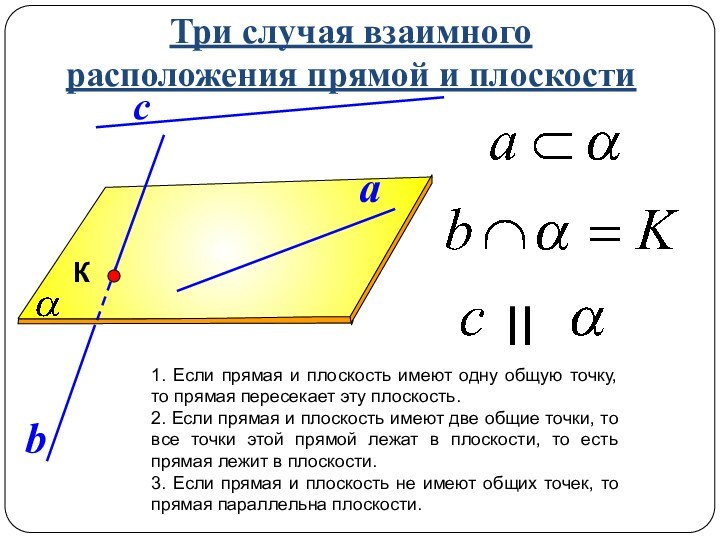
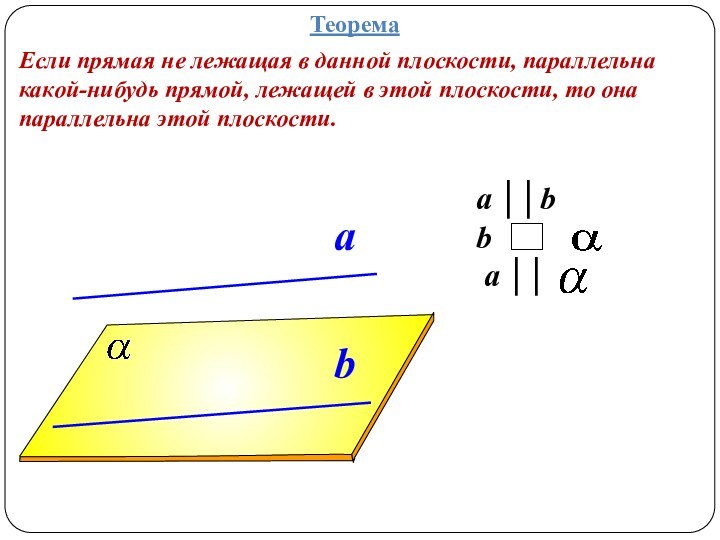
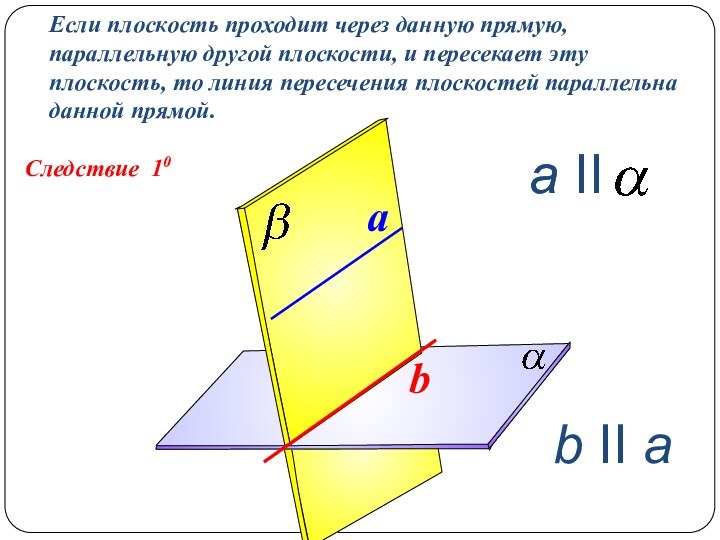
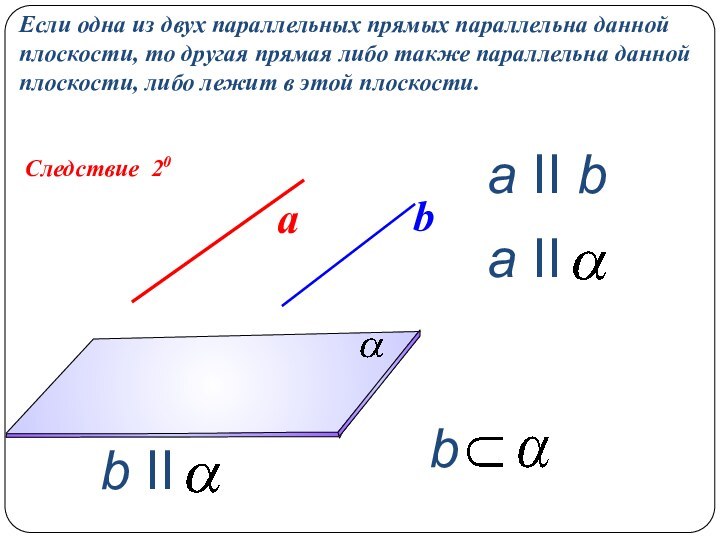

a ΙΙ b
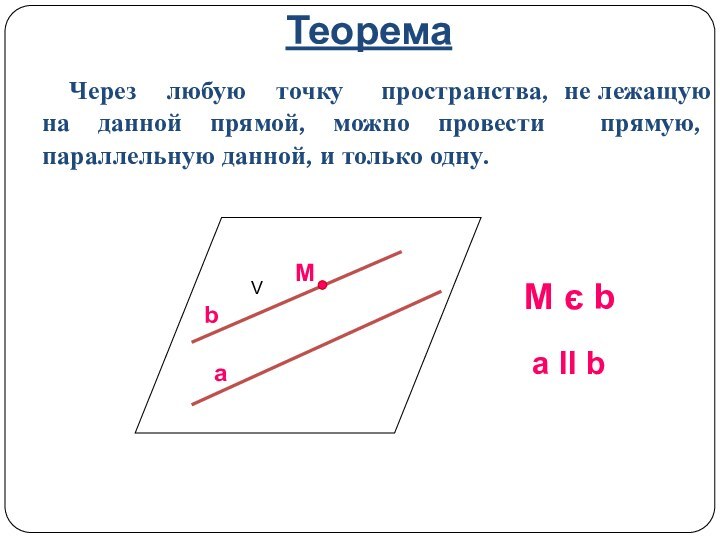
M є b
a ΙΙ b
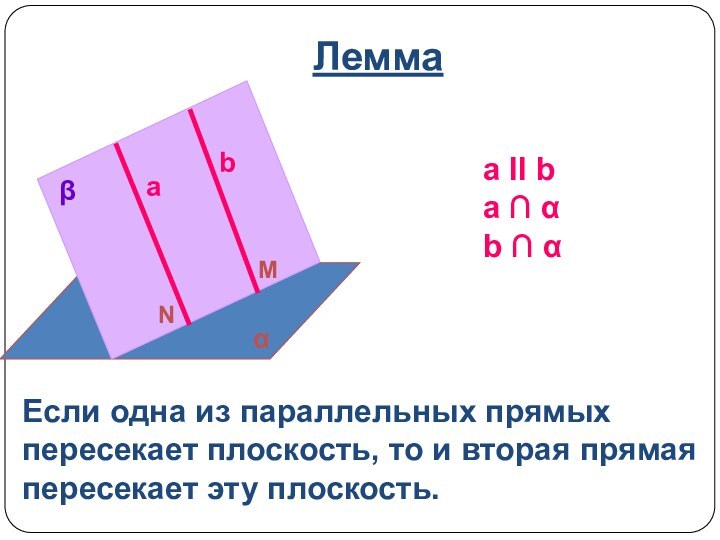
a ΙΙ b
a ΙΙ c
b ΙΙ c
a
b II a
a II b
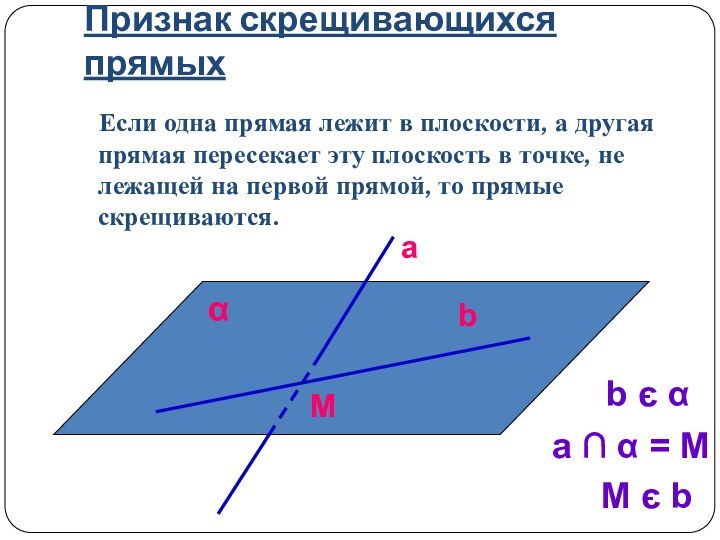
b є α
a ∩ α = M
M є b
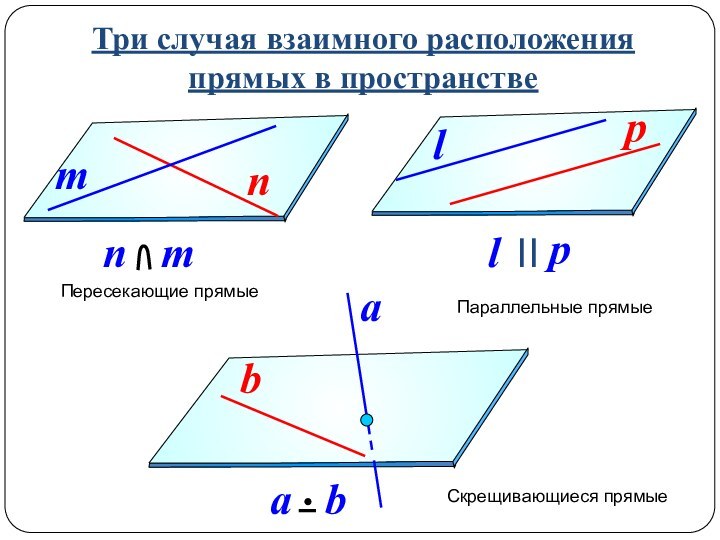
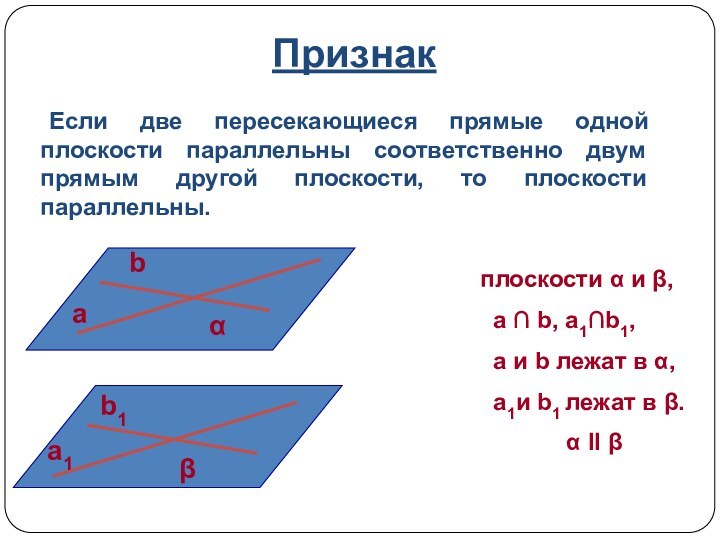
Если две пересекающиеся прямые одной плоскости параллельны соответственно двум прямым другой плоскости, то плоскости параллельны.
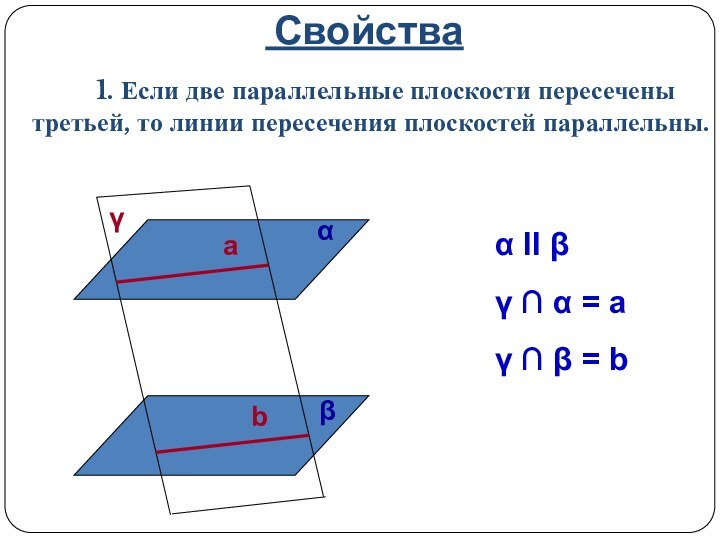
α II β
γ ∩ α = a
γ ∩ β = b
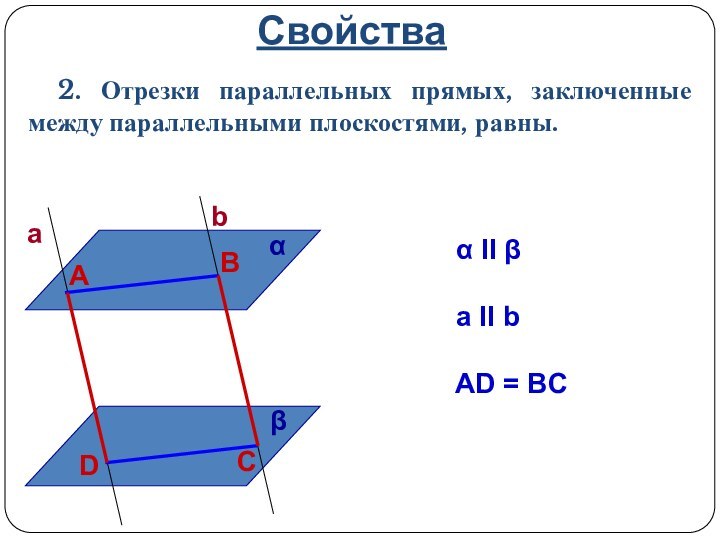
α II β
a II b
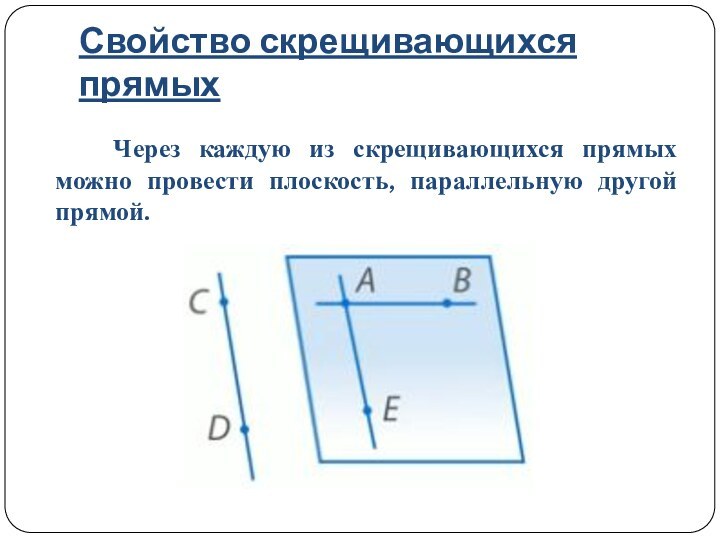
AD = BC
α
β
a
b
А
B
C
D