- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Адаптация и адаптивные методы краткосрочного моделирования. Модель Брауна
Содержание
- 2. Поскольку большие социально-экономические системы, необратимо развиваясь во
- 3. Понятия адаптации и адаптивности появились в лексиконе
- 4. Так, под адаптацией понимается способность системы использовать
- 5. Любая большая система является адаптивной – она
- 6. Поскольку основной задачей социально-экономического прогнозирования является построение
- 7. Впрочем, иногда встречается и такое понятие адаптивной
- 8. Формальной основой алгоритмов адаптации могут быть любые
- 9. В случае краткосрочного прогнозирования задача заключается в
- 10. В случае среднесрочного прогнозирования задача ставится иначе
- 11. Рассмотрим адаптивные методы краткосрочного прогнозирования. Прежде всего,
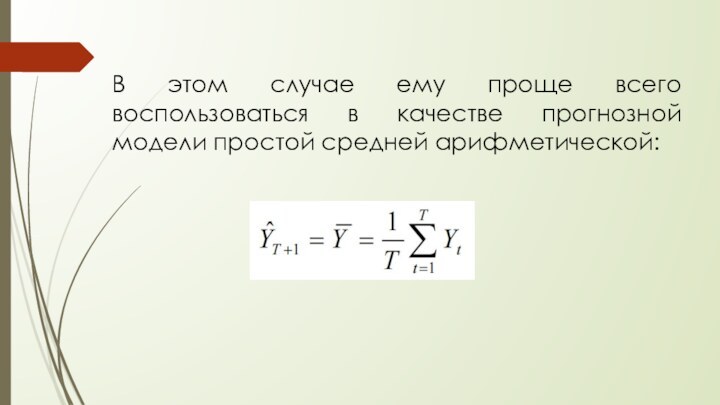
- 12. В этом случае ему проще всего воспользоваться в качестве прогнозной модели простой средней арифметической:
- 13. Эта средняя арифметическая характеризует средний уровень ряда,
- 14. Для эволюционных процессов текущие отклонения являются более
- 15. Если представить в расширенном виде, то получим: Или:
- 16. Здесь vt – вес t-го наблюдения, причём
- 17. Если при этом потребовать выполнения условия (2),
- 18. сходится к единице, то есть его сумма
- 19. Так какой ряд из огромного множества имеющихся
- 20. Перебирать все возможные сходящиеся к единице ряды
- 21. Скачать презентацию
- 22. Похожие презентации
Поскольку большие социально-экономические системы, необратимо развиваясь во времени, адаптируются к различным внешним и внутренним факторам, модели, которые описывают закономерности этого развития, также должны учитывать это свойство, то есть – быть адаптивными. Иначе причинно-следственные связи будут не




















Слайд 3 Понятия адаптации и адаптивности появились в лексиконе экономистов
с приходом в экономику системного анализа. Практически во всех
работах, посвященных анализу свойств больших систем экономики, выявляется свойство адаптивности, то есть – способности к адаптации, приспособлению;самообучаемости и самоорганизуемости.
Слайд 4 Так, под адаптацией понимается способность системы использовать получение
новой информации для приближения своего поведения и структуры к
оптимальным в новых условиях. Самообучение – это способность системы, адаптируясь к новым условиям, корректировать своё поведение с учётом допущенных ошибок.Способность же системы изменять свою структуру, состав и параметры элементов при изменении условий взаимодействия с окружающей средой выделяется как свойство самоорганизуемости.
Слайд 5 Любая большая система является адаптивной – она тем
или иным образом приспосабливается к изменившимся условиям. Но не
каждая из таких систем обладает свойством самообучаемости – приспособления не только на основе внешней информации, но и на основе того, насколько поведение системы далеко от оптимального. Высший уровень живучести большой системы определяется наличием у ней не только свойств адаптивности и самообучаемости, но и самоорганизации.Слайд 6 Поскольку основной задачей социально-экономического прогнозирования является построение прогнозных
моделей, наилучшим способом описывающих динамику развития, то для этого
при прогнозировании эволюционных процессов используют адаптивные методы, под которыми понимают методы, позволяющие в большей степени учитывать текущую информацию и в меньшей степени – прошлую. Основное свойство таких методов – изменение коэффициентов построенной модели при поступлении новой информации, т.е. адаптация моделей к новым данным.Слайд 7 Впрочем, иногда встречается и такое понятие адаптивной корректировки
параметров модели, когда они, оцененные с помощью МНК, при
поступлении новой информации просто пересчитываются вновь. В данном случае нельзя говорить об адаптации, так как последняя предусматривает приспособление моделей к новой информации, учёт её в большей степени, чем прошлой информации, а не простой перерасчет коэффициентов модели с учетом дополнительной информации, которая считается одинаково важной, как в начале наблюдений, так и в ее конце. Это – уточнение модели, а не её адаптация.Слайд 8 Формальной основой алгоритмов адаптации могут быть любые итеративные
методы, позволяющие за конечное количество шагов найти нужное решение.
Именно подобные методы нашли широчайшее применение в задачах технической кибернетики. Но социально-экономические процессы значительно многообразнее задач, которые решаются в технической кибернетике. Применительно к задачам социально-экономического прогнозирования принципиально различными выступают задачи краткосрочного и среднесрочного прогнозирования.Слайд 9 В случае краткосрочного прогнозирования задача заключается в том,
чтобы «уловить» последние по времени сиюминутные отклонения от сложившихся
тенденций, отклонения, которые вызваны кратковременным действием некоторых факторов.После того, как действие этих случайным образом сложившихся факторов прекратиться, показатели социально-экономической системы вновь вернутся к той траектории, по которой они двигались в прежние времена.
Слайд 10 В случае среднесрочного прогнозирования задача ставится иначе –
нет смысла учитывать текущие кратковременные колебания и отклонения от
сложившейся тенденции – они в скором времени прекратятся. Есть смысл «уловить» наметившиеся в последние моменты наблюдений неминуемые изменения в тенденциях развития, и, учитывая их, откорректировать прогнозную модель.Слайд 11 Рассмотрим адаптивные методы краткосрочного прогнозирования. Прежде всего, упростим
задачу – предположим, что перед прогнозистом стоит задача изучить
некоторый временной ряд Yt, не имеющий какой-либо явно выраженной тенденции, и сделать прогноз в конце ряда на один шаг наблюдения Yt+1.Слайд 12 В этом случае ему проще всего воспользоваться в
качестве прогнозной модели простой средней арифметической:
Слайд 13 Эта средняя арифметическая характеризует средний уровень ряда, отклонения
от которого вызваны рядом причин. В случае стационарного процесса,
да ещё при нормальном распределении вероятностей эта процедура не вызывает никаких сомнений и возражений. Но средняя арифметическая, как известно, является наилучшей оценкой математического ожидания процесса только в том случае, когда прогнозируемый процесс является стационарным с нормальным распределением вероятностей. Если эти условия не выполняются, то средняя арифметическая не будет лучшей прогнозной моделью.Слайд 14 Для эволюционных процессов текущие отклонения являются более важными
для понимания происходящих процессов, чем прошлые. Тем более -
текущие значения являются более важными для прогноза, чем прошлые наблюдения. Например, для того, чтобы определить на завтра курс рубля по отношению к евро, текущие значения этого курса важнее, чем значения полугодовалой давности.Слайд 16 Здесь vt – вес t-го наблюдения, причём легко
убедиться в том, что:
Естественное желание учесть текущую информацию
в большей степени, чем прошлую, может быть математически выражено так: Слайд 17 Если при этом потребовать выполнения условия (2), то,
подставляя эти веса в (1), можно получить формулу взвешенной
средней арифметической. В математике существует огромное количество рядов, чья сумма будет равна единице, а каждый вес будет убывать с убыванием наблюдений в прошлое, например, ряд:Слайд 18 сходится к единице, то есть его сумма равна
единице. В принципе любой сходящийся к некоторому числу ряд
можно преобразовать так, чтобы его сумма была равна единице. Например, рядСходится к числу e-1. Поэтому будет равна единице сумма такого ряда: