Слайд 2
При выполнении выше перечисленных операций отношения эквивалентности имеют
вид:
а) дизъюнкция
б) конъюнкция в) инверсия
_
0+0=0 0●0=0 0=1
0+1=1 0●1=0 _
1+0=1 1●0=0 1=0
1+1=1 1●1=1
Слайд 3
Законы алгебры логики:
1. Переместительный закон
для
логического сложения: x1 + x2=
x2 +x1,
для логического умножения: x1 ⋅ x2= x2 ⋅x1.
2. Сочетательный закон
для логического сложения: (x1 + x 2)+x3= x1 +(x2 + x3),
для логического умножения: (x1 ⋅ x 2) x3 = x1(x2⋅x3).
3. Распределительные законы
первый распределительный закон: x1(x2+x3) = x1 ⋅ x2+x1⋅x3, второй распределительный закон: x1+x2⋅x3=(x1+x2)(x1+x3).
Слайд 4
4. Законы отрицания (правило де Моргана)
для дизъюнкции:
x1 + x2 = x1 ⋅ x2
для конъюнкции: x1 ⋅ x2 = x1 + x2
двойное отрицание: x = x
5. Законы поглощения
дизъюнктивное поглощение: x1+x1⋅x2= x1⋅(1+x2)=x1
конъюнктивное поглощение: x1⋅(x1+x2)=x1⋅x1+x1⋅x2=x1+x1⋅x2=x2
6. Законы склеивания
дизъюнктивное склеивание: x1⋅x2+x1⋅x2=x1⋅(x2+x2)=x1
конъюнктивное склеивание: (x1+x2)(x1+x2)=x1+x1⋅ x2+x1⋅x2=x1
Слайд 5
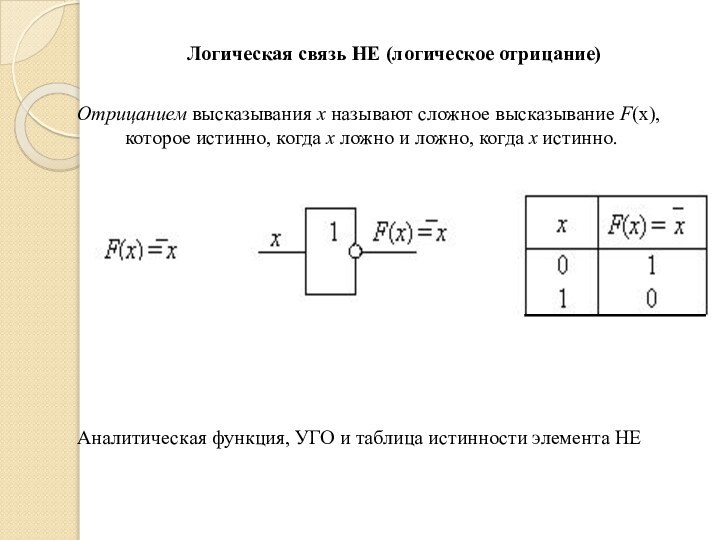
Логическая связь НЕ (логическое отрицание)
Отрицанием высказывания х
называют сложное высказывание F(х), которое истинно, когда х ложно
и ложно, когда х истинно.
Аналитическая функция, УГО и таблица истинности элемента НЕ
Слайд 6
Логическая связь ИЛИ – сложение (дизъюнкция) высказываний
Дизъюнкцией
двух высказываний х1 и х2 называется сложное высказывание F(х1,
х2), которое ложно только в одном случае, когда х1 и х2 одновременно ложны (х1 = 0 и х2 = 0). Во всех остальных случаях высказывание F(х1, х2) истинно.
Аналитическая функция, УГО и таблица истинности элемента ИЛИ
Слайд 7
Логическая связь И (конъюнкция высказываний)
Конъюнкцией высказываний х1
и х2, называется сложное высказывание F(х1, х2), которое истинно
только в одном случае, когда х1 и х2 одновременно истинны (х1 = 1 и х2 = 1). Во всех остальных случаях высказывание F(х1, х2) ложно.
Аналитическая функция, УГО и таблица истинности элемента И
Слайд 8
Логическая связь отрицание дизъюнкции (операция Пирса)
Логической связью
отрицание дизъюнкции высказываний х1 и х2, называется сложное высказывание
F(х1, х2), которое истинно только в том случае, когда х1 и х2 одновременно ложны (х1 = 0 и х2 = 0). Во всех остальных случаях высказывание F(х1, х2) ложно.
Аналитическая функция, УГО и таблица истинности элемента ИЛИ-НЕ
Слайд 9
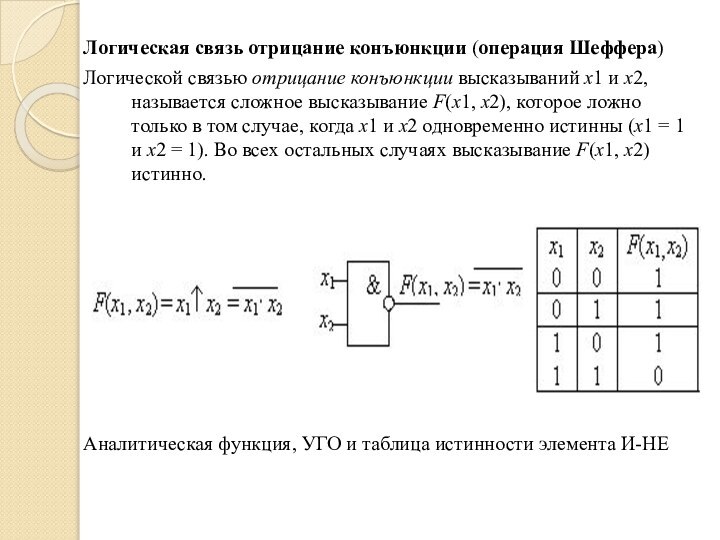
Логическая связь отрицание конъюнкции (операция Шеффера)
Логической связью
отрицание конъюнкции высказываний х1 и х2, называется сложное высказывание
F(х1, х2), которое ложно только в том случае, когда х1 и х2 одновременно истинны (х1 = 1 и х2 = 1). Во всех остальных случаях высказывание F(х1, х2) истинно.
Аналитическая функция, УГО и таблица истинности элемента И-НЕ
Слайд 10
Логическая связь отрицание равнозначности
(операция
ИЛИ-ИЛИ)
Логической связью отрицание равнозначности высказываний х1 и х2,
называется сложное высказывание F(х1, х2), которое истинно тогда, когда значения истинности высказываний х1 и х2 не совпадают и ложно, когда значения истинности высказываний х1 и х2 совпадают.
Аналитическая функция, УГО и таблица истинности элемента исключающее ИЛИ
Слайд 11
СИНТЕЗ ЛОГИЧЕСКИХ СХЕМ
Сущность задач синтеза заключается в том,
чтобы спроектировать логическое устройство
Основные этапы синтеза логических
схем
На первом этапе на основании заданного алгоритма работы синтезируемого устройства формируют словесное описание логической функции.
Пример: Считать, что цель обнаружена (выходной сигнал равен 1) только в тех случаях, когда не менее чем два входных сигнала равны "1". Во всех остальных случаях цель не обнаружена (выходной сигнал равен 0).
Слайд 12
На втором этапе на основе словесной формы логической
функции составляют табличную форму. Затем по таблице истинности находят
аналитическую форму представления логической функции в виде СДНФ или СКНФ
Пример:
СДНФ примет вид :
СКНФ примет вид :
Слайд 13
Третий этап. На этом этапе осуществляется минимизация СДНФ
или СКНФ с целью уменьшения числа логических элементов, необходимых
для разработки функциональной схемы синтезируемого устройства. Для минимизации логических функций используются как аналитические, так и графические методы.
Сущность аналитических методов сводится к последовательному применению законов алгебры логики и их следствий
F(X1,X2,X3)=X2X3(X1+X1)+X1X3(X2+X2)+X1X2(X3+X3) =>
F(X1,X2,X3)=X2X3+X1X3+X1X2
Слайд 14
На четвертом этапе на основе минимизированной логической функции
разрабатывается функциональная схема синтезируемого устройства и проверяется правильность ее
работы.
Слайд 15
Куб Карно
Куб Карно́ — графический способ минимизации переключательных (булевых)
функций, обеспечивающий относительную простоту работы с большими выражениями и
устранение потенциальных гонок. Представляет собой операции попарного неполного склеивания и элементарного поглощения. Карты Карно рассматриваются как перестроенная соответствующим образом таблица истинности функции.
Карты Карно были изобретены в 1952 Эдвардом В. Вейчем и усовершенствованы в 1953 Морисом Карно, физиком из «Bell Labs», и были призваны помочь упростить цифровые электронные схемы.
В карту Карно булевы переменные передаются из таблицы истинности и упорядочиваются с помощью кода Грея, в котором каждое следующее число отличается от предыдущего только одним разрядом
Слайд 16
Принципы минимизации
Основным методом минимизации логических функций, представленных в
виде СДНФ или СКНФ, является операция попарного неполного склеивания и элементарного поглощения.
Операция попарного склеивания осуществляется между двумя термами (членами), содержащими одинаковые переменные, вхождения которых (прямые и инверсные) совпадают для всех переменных, кроме одной. В этом случае все переменные, кроме одной, можно вынести за скобки, а оставшиеся в скобках прямое и инверсное вхождение одной переменной подвергнуть склейке. Например:
Аналогично для КНФ:
Возможность поглощения следует из очевидных равенств
Слайд 17
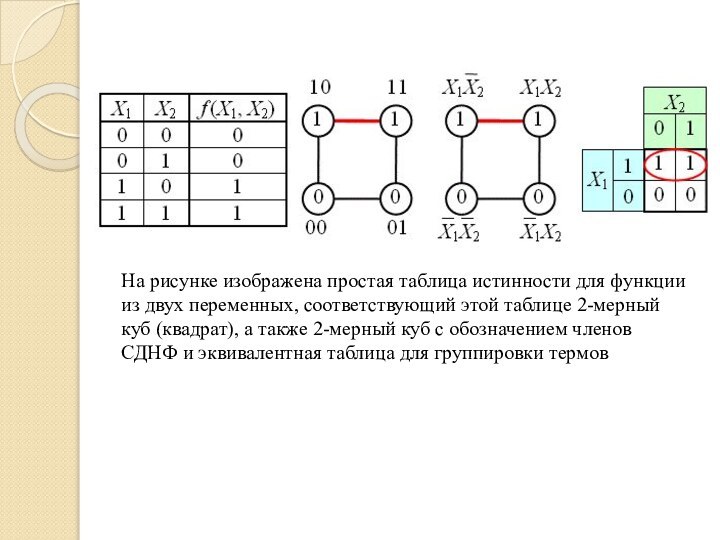
На рисунке изображена простая таблица истинности для функции
из двух переменных, соответствующий этой таблице 2-мерный куб (квадрат),
а также 2-мерный куб с обозначением членов СДНФ и эквивалентная таблица для группировки термов
Слайд 18
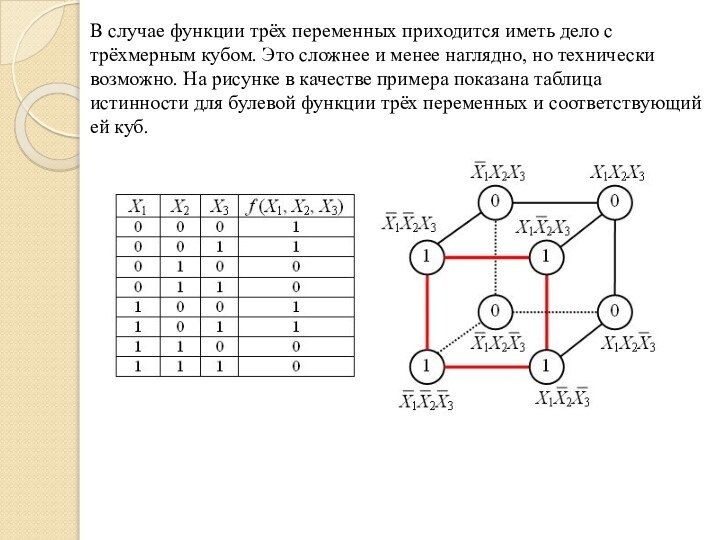
В случае функции трёх переменных приходится иметь дело с
трёхмерным кубом. Это сложнее и менее наглядно, но технически
возможно. На рисунке в качестве примера показана таблица истинности для булевой функции трёх переменных и соответствующий ей куб.
Слайд 19
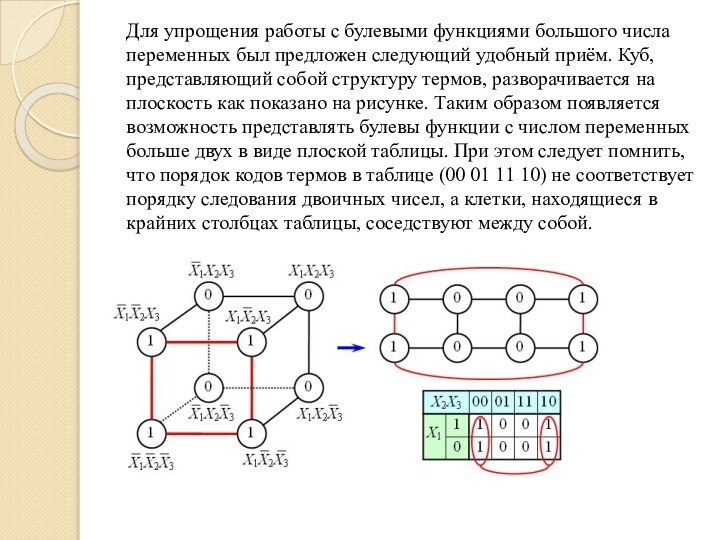
Для упрощения работы с булевыми функциями большого числа
переменных был предложен следующий удобный приём. Куб, представляющий собой
структуру термов, разворачивается на плоскость как показано на рисунке. Таким образом появляется возможность представлять булевы функции с числом переменных больше двух в виде плоской таблицы. При этом следует помнить, что порядок кодов термов в таблице (00 01 11 10) не соответствует порядку следования двоичных чисел, а клетки, находящиеся в крайних столбцах таблицы, соседствуют между собой.
Слайд 20
Синтез логической схемы
Синтезом логической схемы называется процедура получения
логической схемы реализующую заданную логические функцию. При синтезе логических
схем используются логические элементы.
Набор логических функций, с помощью которого можно представить любую переключательную функцию называется функционально полной системой или базисом. Обычно функционально полными системами являются базисы 1) И, ИЛИ, НЕ, 2) И, НЕ, 3) ИЛИ, НЕ, 4) И-ИЛИ-НЕ, 5) И-НЕ, 6) ИЛИ-НЕ.
Основным является базис И, ИЛИ, НЕ так как с помощью него можно записать любую сложную функцию в виде СДНФ и СКНФ.
При синтезе комбинационной схемы с несколькими выходами, каждый выход рассматривается как функция входных значений. Полученные функции минимизируются, и затем строится логическая схема в одном из заданных базисов.
Слайд 21
При синтезе цифровых автоматов , в таблицу функционирования
кроме выходных значений необходимо указывать и внутреннее состояние устройства.
Пример синтеза комбинационной схемы.
Синтезировать комбинационную схему устройства управления семисегментным индикатором в базисе И, ИЛИ, НЕ. Устройство работает согласно таблицы
Слайд 22
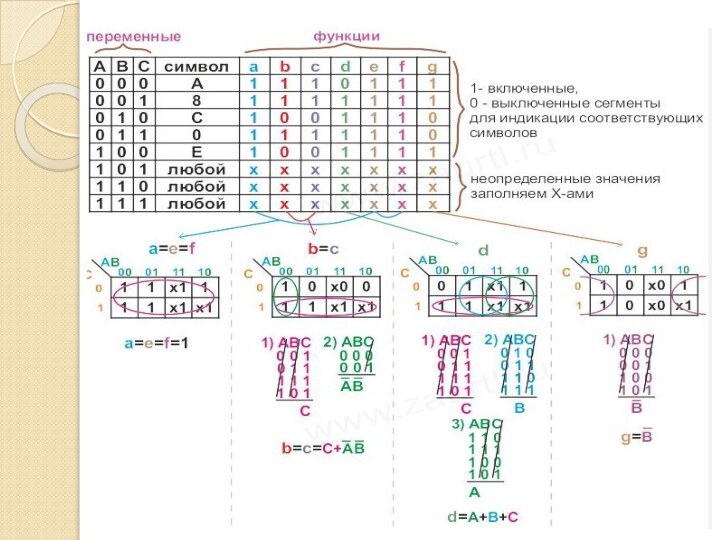
Составляем таблицу функционирования устройства, используя символ индикации и
обозначение сегментов. При этом получаем таблицу зависимости восьми функций
а, b, c, d, e, f, g от переменных (значений входных сигналов). Затем используя карту Карно, получаем минимальные дизъюнктивные форму функций. Неопределенные значения при этом заменяем на «0» или «1» в зависимости от эффективности образования групп и, следовательно, минимизации.
Слайд 24
Используя полученные функции синтезируем логическую схему устройства в
базисе И, ИЛИ, НЕ. Синтез выполняется в направлении от
значений входных сигналов до получения выходных значений. Первоначально из входных переменных получаем необходимые для функций инверсные значения. Затем, поэтапно применяя необходимые элементы для реализации операций, получаем конечные значения функций. Источник логической единиц условно обозначаем точкой (1). При положительной логике ей соответствует напряжение питания всей схемы.