Презентация на тему Анализ количественных признаков

вспомнили общепринятые методы описания и представления данных
На примере

Поговорили о вероятностях возможных ошибок, возникающих при использовании всякого статистического теста

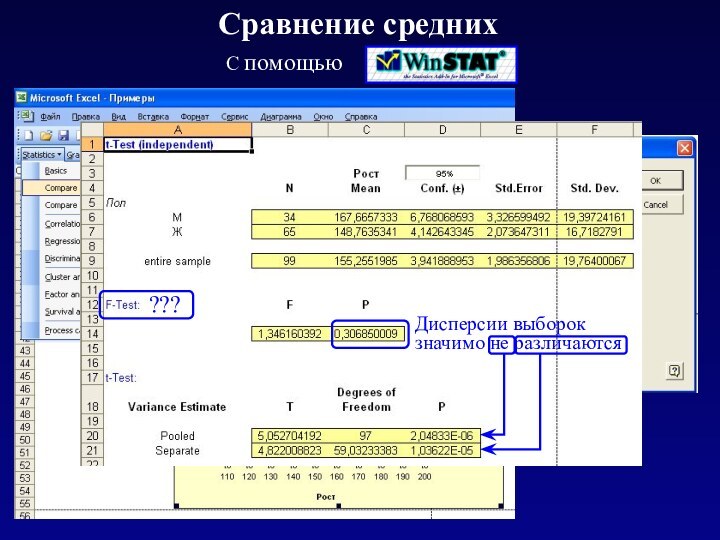
При этом мы сознательно не затрагивали ряд традиционных для статистики тем: сравнение средних, критерий Стьюдента и т.д.

Отчасти потому, что вы об этом наверняка наслышаны, но в основном из методических соображений

средних для двух выборок.
Например, рост в выборках «М» и

Нулевая гипотеза состоит в предположении, что обе выборки изъяты из одной генеральной совокупности (т.е. различий нет):

Н0:

Дальше надо предложить способ оценить вероятность ошибки I рода

универсальный способ построения статистических критериев: Z – статистика, т.е.
Есть

, т.е. разность средних, деленная
на стандартное отклонение этой разности.

но имеет большую дисперсию: D(t) = k/(k-2) >

При k→∞ становится нормальным

Excel умеет вычислять «хвосты» распределения Стьюдента:

= СТЬЮДРАСП(2; 100; 1)

2 означает, что тест двусторонний

0.024

числом
Сравнение двух зависимых выборок
Сравнение двух выборочных средних

Для каждой особи проводят 2 однотипных замера:
- до и после приема лекарства,
- в этом году и в прошлом году и т.д.

Возможно раного объема

3 варианта использования теста Стьюдента:

Медведев сообщил, что средняя продолжительность жизни в РФ составляет

В этом месяце в районном морге побывало 100 клиентов, и получена другая оценка: 62±3 года. Отличается ли эта оценка от средней по стране?

= СТЬЮДРАСП((69-62)/3; 100-1; 2)

Р = 0.022

Вывод: нулевая гипотеза отвергается. Вероятность того, что при этом отвергли правильную нулевую гипотезу равна 0.022 (ошибка I рода). Выборка по данным районного морга не соответствует среднему по стране.
Различия статистически значимы.

2 означает, что тест двусторонний

Эта запись означает, что наша величина имеет распределение Стьюдента с n-1 степенями свободы

Никогда не пишите, что различия достоверны!
Достоверно это то, что происходит с вероятностью 1

В данном примере среднее для одной выборки сравнивалось с заранее известной величиной. Это так называемый одновыборочный тест

(мы это уже делали: помните 470 из 1000?)

случай. Вычисляется t-статистика
и вес хвостов распределения Стьюдента с n1+n2-2

Можно ни о чем этом не думать и использовать

=ТТЕСТ(массив1; массив2; 2; 1)

2 означает, что тест двусторонний

1 означает, что выборки зависимы

Для независимых выборок все несколько сложнее…

возможны 2 ситуации:
σ1 = σ2 ,

σ1 ≠ σ2 , т.е. изменчивость данных в выборках неодинакова, и эти различия статистически значимы. Тогда вычисляется объединенная дисперсия для двух выборок. Число степеней свободы тоже модифицируется.

Не будем расписывать, как это делается, а запустим Excel

=ТТЕСТ(массив1; массив2; 2; 2)

2 означает, что тест двусторонний

2 - σ1 = σ2
3 - σ1 ≠ σ2

Надо сказать, что Excel не проверяет статистическую значимость σ1 ≠ σ2 , Более адекватно поступает WinStat

в случае независимых выборок

возможны 2 ситуации:
σ1 = σ2 ,

σ1 ≠ σ2 , т.е. изменчивость данных в выборках неодинакова, и эти различия статистически значимы. Тогда вычисляется объединенная дисперсия для двух выборок. Число степеней свободы тоже модифицируется.

Не будем расписывать, как это делается, а запустим Excel

=ТТЕСТ(массив1; массив2; 2; 2)

2 означает, что тест двусторонний

2 - σ1 = σ2
3 - σ1 ≠ σ2

Надо сказать, что Excel не проверяет статистическую значимость σ1 ≠ σ2 , Более адекватно поступает WinStat

в случае независимых выборок

ошибки самих оценок (SD и SE)?
Средняя оценка по физике

Средняя оценка по физкультуре = 4.6. Дисперсия = 0.44

Можно записать так 3.40±0.08, но не так 3.4±0.08

Считаем t-статистику:

= СТЬЮДРАСП(11,3; 100-2; 2)

Значимо! Р = 10-19

сравнения дисперсий (F-тест) и вычислил функцию распределения соответствующей статистики.
Не

=ФТЕСТ(массив1; массив2)

=FРАСП(1,5;100;100)

В Excel имеется функция, вычисляющая это распределение

Можно также сравнить дисперсии двух выборок

Н0: σ1 = σ2 против Н1: σ1 < σ2

– сравнение нескольких выборок
Ничего, кроме школьной алгебры!
Средняя дисперсия

Дисперсия средних

Межвыборочная изменчивость

Внутривыборочная изменчивость

Факториальная изменчивость

Остаточная изменчивость

(при k = 2 все сведется к критерию Стьюдента)

Н0:

Н1: хотя бы одно среднее отличается

сравним частоты аберраций хромосом для носителей различных генотипов по

Упражняемся…

сравним частоты аберраций хромосом для носителей различных генотипов по

Упражняемся…

Межгрупповая дисперсия в 12 раз выше, чем внутригрупповая

Можно обойтись пакетом

«Анализ данных» в Excel

результат:
В какой фирме зарплата выше?
=ТТЕСТ(массив1; массив2; 2; 3)
На

Средние

это некорректно…
Средние

т.е. такими, которые не зависят от характера распределения данных.

Самый простой тест – критерий знаков для пары зависимых выборок

0.035

Различия значимы по одностороннему тесту (но не по двустороннему!)

Приводит ли лекарство к увеличению систолического давления?

Манна – Уитни,
который основан на вычислении суммы рангов для

Как всегда Н0: выборки взяты из одной генеральной совокупности.

Упражняемся …

В нашем файле смотрим сопряженность
заболевания с частотой аберраций

Видим различия средних:

Проверяем значимость различий по Стьюденту:

Различия значимы по Стьюденту (независимо от условия равенства дисперсий )

Но что там с нормальностью?

и здоровых:
Какая уж тут нормальностью!
Проверяем значимость различий по Стьюденту:
Различия

Необходимо использовать непараметрический тест Манна-Уитни

Попробуем все это воспроизвести:

различий, о чем с грустью сообщаем в публикации. Достаточно

НЕТ! Мы должны продемонстрировать, что объемы наших выборок достаточны, чтобы обнаружить эффект, если он существует.

Мощность (чувствительность) используемых тестов должна быть не ниже 80% (тогда упускаем не более 20% открытий)

Только в этом случае незначимые различия можно рассматривать как отрицательный результат

Compare2/ Numerical observations/

Тогда по тесту Стьюдента различия незначимы и Р = 0.159

Проверим мощность данного теста

Compare2/ Power/ Comparison of means
Size A - 100 Size B – 100
DETECT a difference 2

Чтобы выйти на мощность 80% объемы выборок должны быть 400 и 400

Compare2/ Sample size/ Means

Допустим, что для 2 выборок имеем:

О чем мы обязаны сообщить в публикации (правда биологи этого почти никогда не делают)

т.е. доля упущенных открытий более 70% !