Что такое findslide.org?

FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.

Для правообладателей

Обратная связь

Email: Нажмите что бы посмотреть 

Яндекс.Метрика

Презентация на тему Арифметические операции в системах

Содержание

1 – 10 2 - 5 3 - 4 4 - 1 5 - 2 6 - 8 7 - 3
Ум заключается не только в знании, но и в умении 1 – 10 2 - 5 3 - 4 4 - 1 Укажите, какие числа записаны с ошибками и аргументируйте ответ: 1237, 30064, 12ААС0920, Арифметические операции в системах счисления Сложение в позиционных системах счисления Цифры суммируются по разрядам, Примеры:10011001010110 Примеры1 3 1 12 3 5 2 Пример:С В А16+ A 5 9161 7 1 3 Вычитание в позиционных системах счисления При вычитании чисел, если Примеры:111011110 Примеры5 0 42 7 4 Пример:А 5 916– 1 В А16 8 9 F 3∙3=9=8+1Умножение в позиционных системах счисления При умножении многозначных чисел Деление в позиционных системах счисления Деление в любой позиционной Примеры:×111102:1102=1011011101 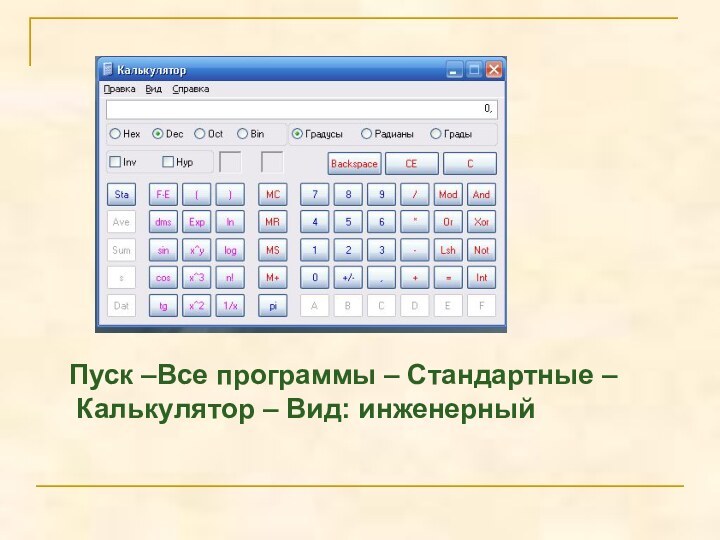Пуск –Все программы – Стандартные – Калькулятор – Вид: инженерный Домашнее заданиеПараграф 2.8№ 2.25 Сегодня на уроке самым познавательным для меня было …Меня удивило, что …Полученные
Слайды презентации

Слайд 2 1 – 10 2 - 5 3 - 4 4 -

1 – 10 2 - 5 3 - 4 4 -

1 5 - 2 6 - 8 7 - 3

Слайд 3 Укажите, какие числа записаны
с ошибками и аргументируйте

Укажите, какие числа записаны с ошибками и аргументируйте ответ: 1237, 30064,

ответ: 1237, 30064, 12ААС0920, 134767
Какое минимальное основание должна иметь
система

счисления, если в ней
могут быть записаны числа: 10, 21, 201, 1201

Какой цифрой заканчивается четное двоичное число? Какой цифрой заканчивается нечетное двоичное число?

Слайд 4 Арифметические операции в системах счисления

Арифметические операции в системах счисления

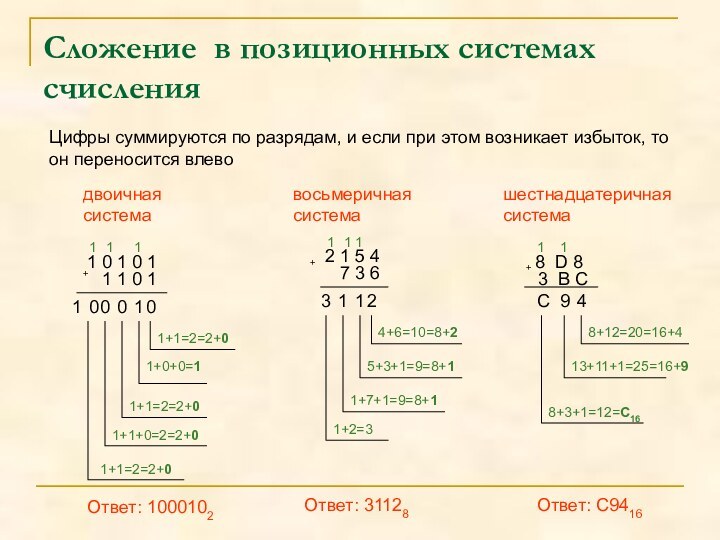
Слайд 5 Сложение в позиционных системах счисления

Сложение в позиционных системах счисления Цифры суммируются по разрядам, и


Цифры суммируются по разрядам, и если при этом возникает

избыток, то он переносится влево

1 0 1 0 1

+

1 1 0 1

двоичная
система

0


1+1=2=2+0

1

1


1+0+0=1

0


1+1=2=2+0

1

0


1+1+0=2=2+0

1

0


1+1=2=2+0

1

Ответ: 1000102

2 1 5 4

+

7 3 6

2


4+6=10=8+2

1

1


5+3+1=9=8+1

1


1+7+1=9=8+1

1

3


1+2=3

восьмеричная
система

1

Ответ: 31128

шестнадцатеричная
система

8 D 8

+

3 B C

4


8+12=20=16+4

1

9


13+11+1=25=16+9


8+3+1=12=C16

C

1

Ответ: C9416

Слайд 6 Примеры:
1001100
1010110

Примеры:10011001010110

Слайд 7 Примеры
1 3 1 1
2 3 5 2

Примеры1 3 1 12 3 5 2

Слайд 8 Пример:
С В А16
+ A 5 916

1 7

Пример:С В А16+ A 5 9161 7 1 3

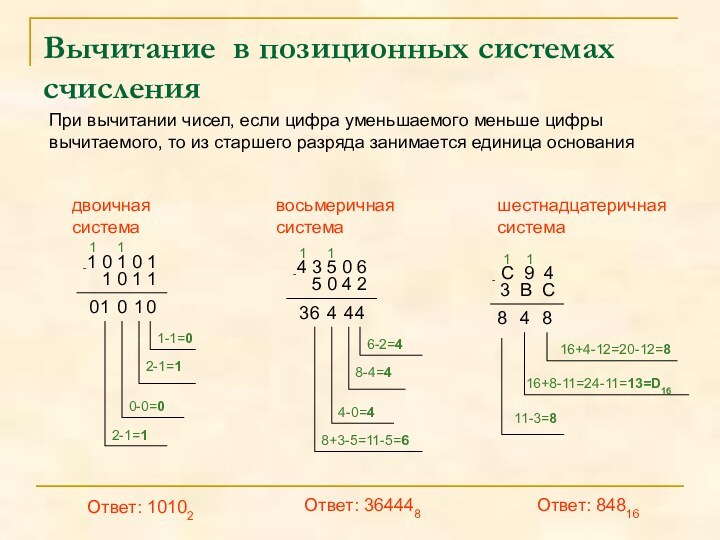
Слайд 9 Вычитание в позиционных системах счисления

Вычитание в позиционных системах счисления При вычитании чисел, если цифра


При вычитании чисел, если цифра уменьшаемого меньше цифры вычитаемого,

то из старшего разряда занимается единица основания

двоичная
система

Ответ: 10102

восьмеричная
система

Ответ: 364448

шестнадцатеричная
система

Ответ: 84816

1 0 1 0 1

-

1 0 1 1

0


1-1=0

1

1


2-1=1

0


0-0=0

1


2-1=1

1

0

4 3 5 0 6

-

5 0 4 2

4


6-2=4

1

4


8-4=4

4


4-0=4

6


8+3-5=11-5=6

1

3

С 9 4

-

3 В С

8


16+4-12=20-12=8

1

4


16+8-11=24-11=13=D16

8


11-3=8

1

Слайд 10 Примеры:
1110
11110

Примеры:111011110

Слайд 11 Примеры
5 0 4
2 7 4

Примеры5 0 42 7 4

Слайд 12 Пример:
А 5 916
– 1 В А16

8

Пример:А 5 916– 1 В А16 8 9 F

Слайд 13 3∙3=9=8+1
Умножение в позиционных системах счисления

3∙3=9=8+1Умножение в позиционных системах счисления При умножении многозначных чисел в


При умножении многозначных чисел в различных позиционных системах применяется

алгоритм перемножения чисел в столбик, но при этом результаты умножения и сложения записываются с учетом основания системы счисления

двоичная
система

Ответ: 1010111112

восьмеричная
система

Ответ: 133518

1 1 0 1 1

х

1 1 0 1

1 1 0 1 1

1 1 0 1 1

1 1 0 1 1


1 0 1 0 1 1 1 1 1


1+1+1=3=2+1

1


1+1+1=3=2+1

1


1+1=2=2+0

1

1

1 6 3

х

6 3

5 3 1


1


6∙3+1=19=16+3=2∙8+3

2


1∙3+2=5

1 2 6 2



6∙3=18=16+2=8∙2+2


6∙6+2=38=32+6=4∙8+6


2

4

6∙1+4=10=8+2

1 3 3 5 1


6+5=11=8+3

1

Слайд 14 Деление в позиционных системах счисления

Деление в позиционных системах счисления Деление в любой позиционной системе


Деление в любой позиционной системе производится по тем же

правилам, как и деление углом в десятичной системе. При этом необходимо учитывать основание системы счисления.

двоичная
система

Ответ: 10,12

восьмеричная
система

Ответ: 638


1 0 0 0 1 1



1 1 1 0

1

1 1 1 0

1 1 1 0

1 1

1

,

0

0

1

0

1 3 3 5 1

1 6 3

6

1 2 6 2

5 3

1

3

5 3 1

0

Слайд 15 Примеры:
×
111102:1102=

1011011
101

Примеры:×111102:1102=1011011101

Слайд 16
Пуск –Все программы – Стандартные –
Калькулятор –

Пуск –Все программы – Стандартные – Калькулятор – Вид: инженерный

Вид: инженерный

Слайд 17 Домашнее задание
Параграф 2.8
№ 2.25

Домашнее заданиеПараграф 2.8№ 2.25
  • Имя файла: arifmeticheskie-operatsii-v-sistemah.pptx
  • Количество просмотров: 97
  • Количество скачиваний: 0
- Предыдущая Проект Конституции 1993 года
Следующая - Строим свое здоровье сами

Похожие презентации

Многочлен и его стандартный вид Многочлен и его стандартный вид 115
Презентация ГЕОМЕТРИЯ ВОКРУГ НАС презентация к уроку математики (4 класс) по теме Презентация ГЕОМЕТРИЯ ВОКРУГ НАС презентация к уроку математики (4 класс) по теме 186
Равные множества. Пустое множество. Знак Ø Равные множества. Пустое множество. Знак Ø 159
Подібність трикутників Подібність трикутників 102
презентация- блоки Дьенеша презентация (математика) по теме презентация- блоки Дьенеша презентация (математика) по теме 108
Презентация по математике на тему: Правильные и неправильные дроби (5 класс) Презентация по математике на тему: Правильные и неправильные дроби (5 класс) 134
Транежёр по математике Помоги принцессе! Транежёр по математике Помоги принцессе! 111
Презентация по математике по теме Нумерация в пределах 100 Презентация по математике по теме Нумерация в пределах 100 165
1 класс. Презентация.Задача в два действия презентация к уроку по математике (1 класс) 1 класс. Презентация.Задача в два действия презентация к уроку по математике (1 класс) 96
Решение задач Закрепление 2 класс Решение задач Закрепление 2 класс 101
Подготовка к ЕГЭ 2012. Диаграммы и графики Подготовка к ЕГЭ 2012. Диаграммы и графики 156
Математика: Проценты Математика: Проценты 151
Сечение Сечение 90
Презентация к уроку математики в 5 классе по теме Решение задач на уравнивание с использованием приёмов холистического обучения Презентация к уроку математики в 5 классе по теме Решение задач на уравнивание с использованием приёмов холистического обучения 113
Презентация по теме Решение упражнений с использованием положительных и отрицательных чисел 6 класс Презентация по теме Решение упражнений с использованием положительных и отрицательных чисел 6 класс 123
Пропорция. Решение задач Пропорция. Решение задач 112
Неравенства-подготовка к ЕГЭ Неравенства-подготовка к ЕГЭ 121
Возрастание убывание функции Возрастание убывание функции 132
Построение сечения куба, нахождение его координат и площади Построение сечения куба, нахождение его координат и площади 122
Презентация к уроку математики Умножение обыкновенных дробей 5 класс Презентация к уроку математики Умножение обыкновенных дробей 5 класс 205
Умножение числа на сумму план-конспект урока по математике (4 класс) Умножение числа на сумму план-конспект урока по математике (4 класс) 143
Сравнение двузначных чисел Сравнение двузначных чисел 111
Основные аксиомы стереометрии Основные аксиомы стереометрии 116
Математика. Решение задач. 2 класс Школа России презентация к уроку математики (2 класс) по теме Математика. Решение задач. 2 класс Школа России презентация к уроку математики (2 класс) по теме 152
Тема урока: НАХОЖДЕНИЕ Площади ФИГУР и объемОВ ТЕЛ Тема урока: НАХОЖДЕНИЕ Площади ФИГУР и объемОВ ТЕЛ 114
Геометрические фигуры презентация к уроку по математике (старшая группа) Геометрические фигуры презентация к уроку по математике (старшая группа) 111
Теорема о трех перпендикулярах Теорема о трех перпендикулярах 127
Конспект и презентация к уроку математики Таблица умножения и деления с числом 5 план-конспект урока по математике (3 класс) по теме Конспект и презентация к уроку математики Таблица умножения и деления с числом 5 план-конспект урока по математике (3 класс) по теме 130
10-га, 100-ке,1000-га артыышкынныг үлелге. план-конспект урока по математике (4 класс) 10-га, 100-ке,1000-га артыышкынныг үлелге. план-конспект урока по математике (4 класс) 169
Презентация по математике на тему Простые и составные числа Презентация по математике на тему Простые и составные числа 132