Слайд 2
Пояснительная записка
Данный элективный курс разработан в
рамках предпрофильной подготовки для ориентации учебно-воспитательного процесса на удовлетворение
потребностей учащихся в углублении их знаний, умений и навыков по математике и готовит обучающихся к переходу в старшем звене на профильный уровень обучения.
Курс ориентирован на развитие у школьника умений решать задачи практического характера. Он развивает умение работать с информацией, представленной в виде таблиц, графиков, диаграмм, производить интерпретацию результатов, полученных при исследованиях и опросах общественного мнения.
Слайд 3
Цель и задачи:
Целью данного элективного курса является
формирование у учащихся первоначальных вероятностно-статистических представлений.
В процессе изучения
курса решаются следующие задачи:
получение знаний о комбинаторике и основных элементах теории вероятностей;
овладение умениями решать задачи, связанные с конкретной жизненной ситуацией;
умение определять связь теории вероятностей с практическими потребностями.
Слайд 4
Формы организации учебных занятий
На занятиях предполагается использование
различных форм активного обучения: игры, учебные исследования, опрос общественного
мнения, проведение опытов, интерактивные занятия, создание мини-проекта.
Формы контроля:
Текущий контроль проводится в форме собеседования с
учащимися по решению практических задач.
Тематический контроль предполагает проверку выполнения тестовых заданий.
Итоговый контроль происходит в форме защиты проекта по теме элективного курса, создается буклет «Задачи по статистике, комбинаторике и теории вероятностей».
Слайд 5
Формы контроля за уровнем достижений обучающихся:
Текущий контроль осуществляется
в ходе выполнения практических работ во время занятий;
Достижения обучающихся
по итогам прохождения элективного курса оцениваются по последнему продуктивному заданию, которым завершается практическая работа над всей темой.
Слайд 6
Требования к подготовке учащихся:
В результате изучения курса ученик
должен знать/понимать:
1. Выбрать и применить более рациональный способ решения
той или иной логической задачи.
2. Использовать свои знания из различных школьных предметов при решении задач по теории множеств и математической логики.
3. Уметь вычислять вероятности событий, пользуясь различными определениями вероятности и формулами.
4. Видеть в конкретных научных, технических, житейских проблемах вопросы, задачи, допускающие решения методами теории вероятностей, уметь формулировать и решать такие задачи.
Слайд 7
На контроле следующие виды деятельности учащихся:
Работы над проектом:
умение
отобрать материал
изложить теорию вопроса
решить круг задач самостоятельно на применение
этой теории
умение изложить данный материал на занятии в группе
умение ответить на вопросы одноклассников
Слайд 8
Основные методические особенности:
Подготовка по тематическому принципу, соблюдая «правила
спирали» от простых типов заданий к сложным;
Работа с
тематическими тестами, выстроенными в виде логически взаимосвязанной системы;
Работа с тренировочными тестами в режиме «теста скорости»;
Работа с тренировочными тестами в режиме максимальной нагрузки, как по содержанию, так и по времени.
Слайд 9
Содержание тем учебного курса
Слайд 10
Описание материально-технического обеспечения образовательного процесса
А. А. Чернов, А.Ф.
Чернов. Начальные сведения из теории вероятностей. Сборник элективных курсов.
Волгоград: Учитель, 2014.
Макарычев Ю. В., Миндюк Н. Г. Элементы статистики и теории вероятностей. – М.: Просвещение, 2009.
Мордкович А.Г., Семенов П.В. События. Вероятности. Статистика обработки данных .7-9 класс.- М.: Мнемозина, 2010.
Ткачева М. В., Федорова Н.Е. Элементы статистики и вероятность. – М.: Просвещение, 2013.
Слайд 11
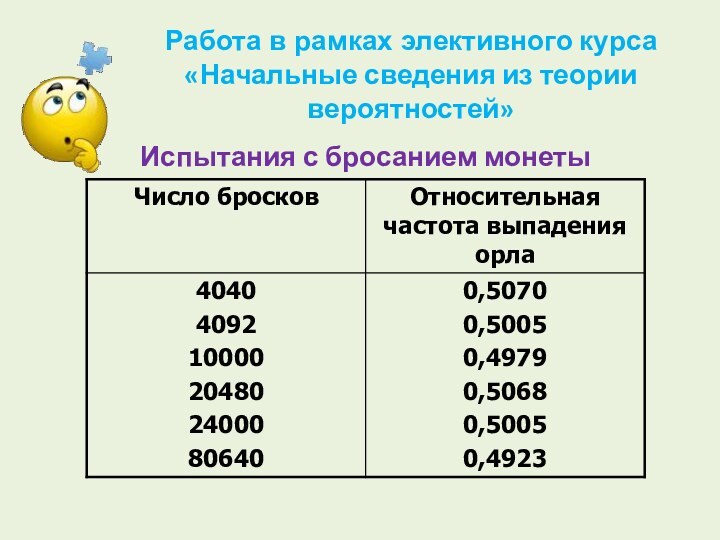
Испытания с бросанием монеты
Работа в рамках элективного курса
«Начальные
сведения из теории вероятностей»
Слайд 12
Работа в рамках элективного курса
«Начальные сведения из теории
вероятностей»
Задача.
На полке стоят 12 книг, из которых
4 – это учебники. С полки снимают наугад 6 книг. Какова вероятность того, что 3 из них окажутся учебниками?
Решение:
Пусть А – событие, состоящее в том, 3 из 6 снятых с полки книг, окажутся учебниками, тогда количество равновозможных исходов «снять 6 книг из 12» равно С126 при этом количество благоприятных исходов «снять 3 учебника из 4» равно С43, после чего количество благоприятных исходов «снять 3 неучебника из 8 неучебников» равно С83 и по правилу комбинаторного умножения всего благоприятных исходов события А будет С43С83.
Значит Р(А) = С43С83/С126 = (4!/3!1!)(8!/3!5!)/(12!/6!6!) = 4!8!6!6!/(3!3!5!12!) = 8:33 =24%.