Что такое findslide.org?

FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.

Для правообладателей

Обратная связь

Email: Нажмите что бы посмотреть 

Яндекс.Метрика

Презентация на тему Призма. Элементы призмы

Содержание

ПризмыПризма - Призмой называется многогранник у которого грани находятся в параллельных плоскостях.Чертёж призмы
Презентация На тему: ПризмаДанную презентацию сделали ученики «9Б» класса:Харчевников Андрей Ильин Костя Артёменко Егор ПризмыПризма - Призмой называется многогранник у которого грани находятся в параллельных плоскостях.Чертёж призмы Элементы призмы Элементы призмыОснования – это грани, совмещаемые параллельным переносом.Боковая грань – это грань, Общие свойства призмыОснования призмы равныОснования призмы лежат в параллельных плоскостяхУ призмы боковые Виды призмn –n –угольная призма Прямая призмаНаклонная призмаПравильная призма N-угольная призма- это призма, в основании которой лежит n -угольникТреугольная призмаЧетырёхугольная призмаШестиугольная призма Прямая призма- это призма, боковые рёбра которой перпендикулярны основаниюЕё высота равна боковому ребруb Правильная призма- это прямая призма, основанием которой является правильный многоугольник.В основании равносторонний Наклонная призма- это призма, боковые рёбра которой не перпендикулярны основанию. Поверхность призмыПолная поверхность Sполн.Поверхность – это сумма площадей граней+ Боковая поверхность прямой призмыТеорема: Боковая поверхность прямой призмы равна произведению периметра Особые сечения призмыДиагональное сечение – это сечение проходящее через два боковых ребра, Призмы вокруг нас
Слайды презентации

Слайд 2 Призмы
Призма -
Призмой называется многогранник у которого грани

ПризмыПризма - Призмой называется многогранник у которого грани находятся в параллельных плоскостях.Чертёж призмы

находятся в параллельных плоскостях.

Чертёж призмы

Слайд 3 Элементы призмы




Элементы призмы

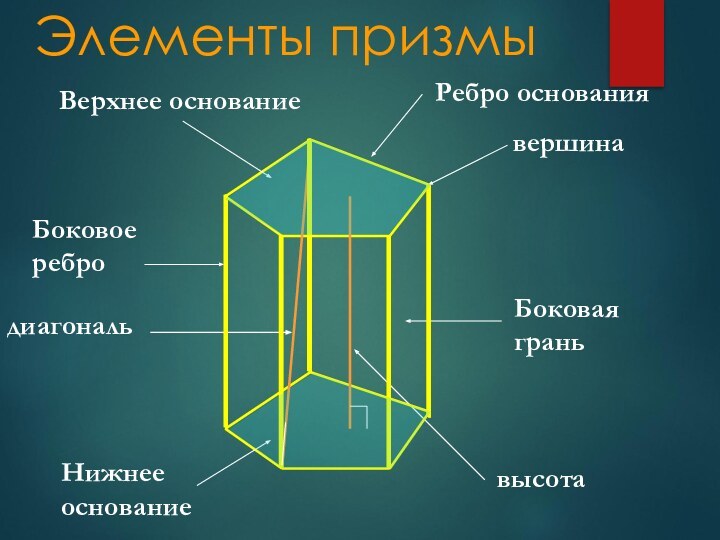
Слайд 4 Элементы призмы
Основания –
это грани, совмещаемые параллельным переносом.
Боковая

Элементы призмыОснования – это грани, совмещаемые параллельным переносом.Боковая грань – это

грань –
это грань, не являющаяся основанием.
Боковые рёбра –


это отрезки, соединяющие соответствующие вершины оснований.
Вершины –
это точки, являющиеся вершинами оснований.
Высота –
это перпендикуляр, опущенный из одного основания на другое.
Диагональ –
это отрезок, соединяющий две вершины, не лежащие в одной грани.

Слайд 5 Общие свойства призмы
Основания призмы равны
Основания призмы лежат в

Общие свойства призмыОснования призмы равныОснования призмы лежат в параллельных плоскостяхУ призмы

параллельных плоскостях
У призмы боковые рёбра параллельны и равны
Любая боковая

грань является параллелограммом


Слайд 6 Виды призм
n –n –угольная призма

Прямая призма

Наклонная призма

Правильная

Виды призмn –n –угольная призма Прямая призмаНаклонная призмаПравильная призма

призма

Слайд 7 N-угольная призма
- это призма, в основании которой лежит

N-угольная призма- это призма, в основании которой лежит n -угольникТреугольная призмаЧетырёхугольная призмаШестиугольная призма

n -угольник
Треугольная призма
Четырёхугольная призма
Шестиугольная призма

Слайд 8 Прямая призма
- это призма, боковые рёбра которой перпендикулярны

Прямая призма- это призма, боковые рёбра которой перпендикулярны основаниюЕё высота равна боковому ребруb

основанию
Её высота равна
боковому ребру
b

Слайд 9 Правильная призма
- это прямая призма, основанием которой является

Правильная призма- это прямая призма, основанием которой является правильный многоугольник.В основании

правильный многоугольник.
В основании равносторонний треугольник
В основании квадрат
В основании правильный


6-угольник

Слайд 10 Наклонная призма
- это призма, боковые рёбра которой не

Наклонная призма- это призма, боковые рёбра которой не перпендикулярны основанию.

перпендикулярны основанию.

Слайд 11 Поверхность призмы
Полная поверхность Sполн.







Поверхность – это сумма площадей

Поверхность призмыПолная поверхность Sполн.Поверхность – это сумма площадей граней+

граней
+

Слайд 12 Боковая поверхность прямой призмы
Теорема:
Боковая поверхность прямой

Боковая поверхность прямой призмыТеорема: Боковая поверхность прямой призмы равна произведению периметра основания на длину бокового ребра.

призмы равна произведению периметра основания на длину бокового ребра.

Слайд 13 Особые сечения призмы
Диагональное сечение – это сечение проходящее

Особые сечения призмыДиагональное сечение – это сечение проходящее через два боковых

через два боковых ребра, не принадлежащих одной грани.
Перпендикулярное сечение

– это сечение, проходящее перпендикулярно боковым ребрам.
  • Имя файла: prizma-elementy-prizmy.pptx
  • Количество просмотров: 152
  • Количество скачиваний: 0
- Предыдущая Disorders of nucleoproteids metabolism. Disorder of metabolism of haemoglobinogenic pigments
Следующая - Стратегии ценообразования

Похожие презентации

Конспект урока Двузначные числа. Повторение (Школа России, 2 класс) план-конспект урока по математике (2 класс) Конспект урока Двузначные числа. Повторение (Школа России, 2 класс) план-конспект урока по математике (2 класс) 157
Таблица сложения презентация к уроку по математике (1 класс) Таблица сложения презентация к уроку по математике (1 класс) 111
Презентация по математике Деление чисел с разными знаками (6 класс) Презентация по математике Деление чисел с разными знаками (6 класс) 123
Что такое дроби? Что такое дроби? 112
Презентация к внеклассному мероприятию по теме День программиста Презентация к внеклассному мероприятию по теме День программиста 169
Учись считать Учись считать 89
Связь математики с другими науками Связь математики с другими науками 177
Симметрия Симметрия 102
Использование игровых моментов при повторении на уроках математики в 5-ых классах Использование игровых моментов при повторении на уроках математики в 5-ых классах 119
Определение параллельных прямых Определение параллельных прямых 89
Математические ребусы Математические ребусы 96
Презентация Во сколько раз больше,во сколько раз меньше. презентация к уроку по математике Презентация Во сколько раз больше,во сколько раз меньше. презентация к уроку по математике 168
Тренажёр по математике Решу ВПР: прямоугольный параллелепипед, куб (часть 3) Тренажёр по математике Решу ВПР: прямоугольный параллелепипед, куб (часть 3) 142
Находим неизвестное презентация к уроку по математике (4 класс) Находим неизвестное презентация к уроку по математике (4 класс) 136
Значения выражений Значения выражений 116
Число и цифра 8 Число и цифра 8 118
Тренажёр по математике 3 класс Умножение на 10, 100 и 1000 тест по математике (3 класс) Тренажёр по математике 3 класс Умножение на 10, 100 и 1000 тест по математике (3 класс) 139
Деление 5 класс Деление 5 класс 109
Зерттеудің нәтижелерін. Талдау Зерттеудің нәтижелерін. Талдау 103
Свойства сложения натуральных чисел. Свойства сложения натуральных чисел. 108
Комфортность на урокх математики Комфортность на урокх математики 125
Определённый интеграл. Введение и некоторые его приложения Определённый интеграл. Введение и некоторые его приложения 107
Дециметр 1 класс Дециметр 1 класс 198
Технологическая карта по математике 2 класс план-конспект урока по математике (2 класс) Технологическая карта по математике 2 класс план-конспект урока по математике (2 класс) 49
Новые приключения Волка и поросят Новые приключения Волка и поросят 115
Конспект интегрированного занятия в подготовительной группе Полет на Луну план-конспект занятия по математике (подготовительная группа) по теме Конспект интегрированного занятия в подготовительной группе Полет на Луну план-конспект занятия по математике (подготовительная группа) по теме 101
Вращательные движение твердого тела Вращательные движение твердого тела 154
Формирование математической грамотности и читательской компетентности с помощью современных образовательных технологий презентация по математике Формирование математической грамотности и читательской компетентности с помощью современных образовательных технологий презентация по математике 127
Математика-царица наук Математика-царица наук 199
Математика. Решение задач. 2 класс Школа России презентация к уроку математики (2 класс) по теме Математика. Решение задач. 2 класс Школа России презентация к уроку математики (2 класс) по теме 150