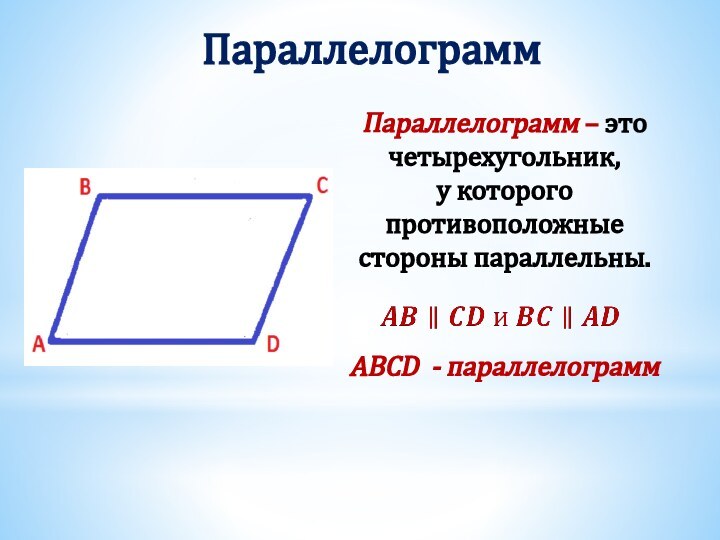
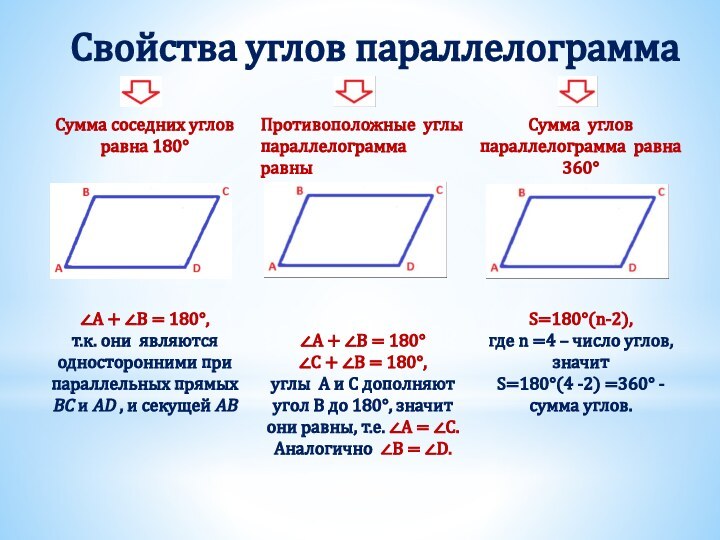
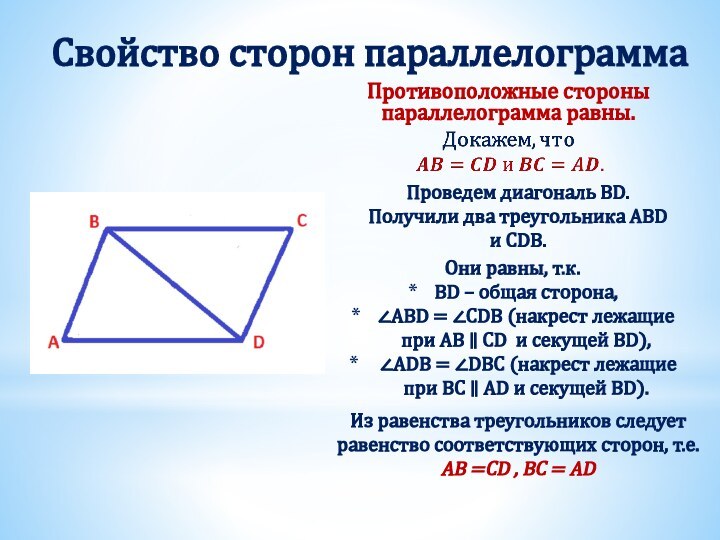
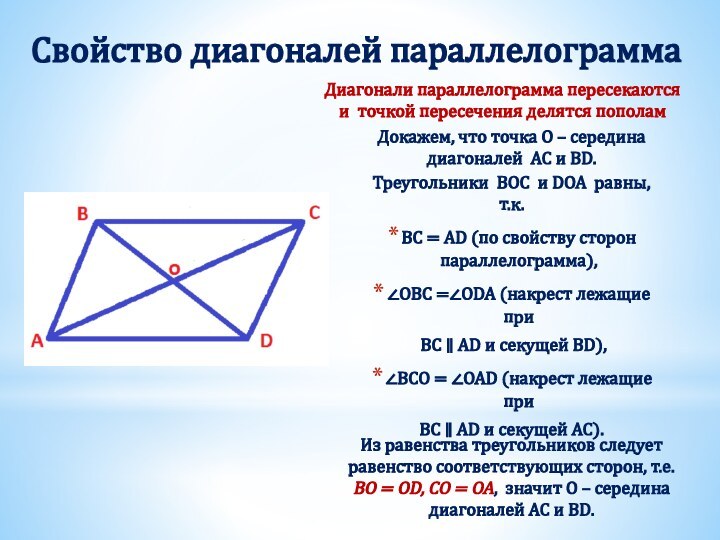
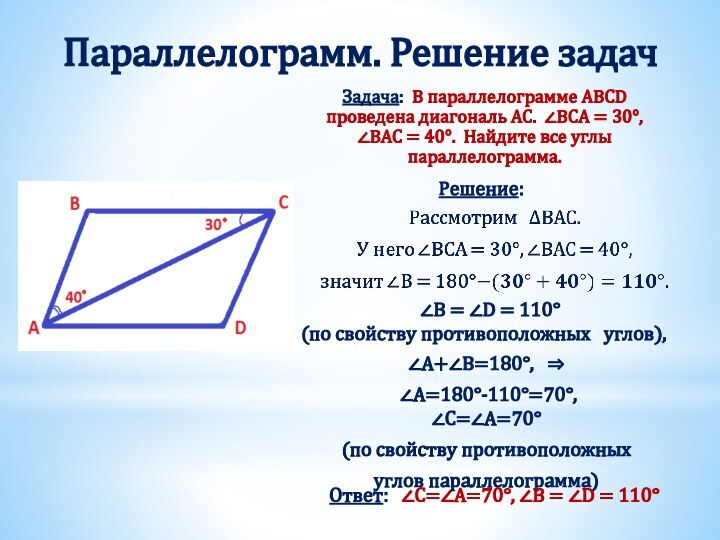
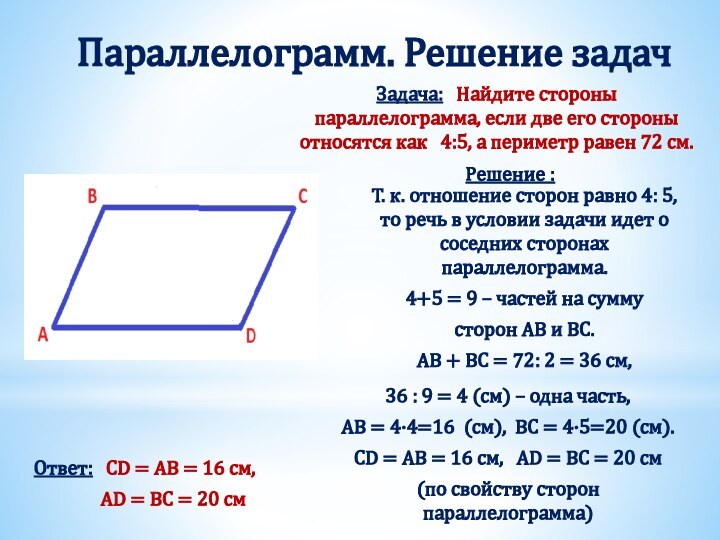
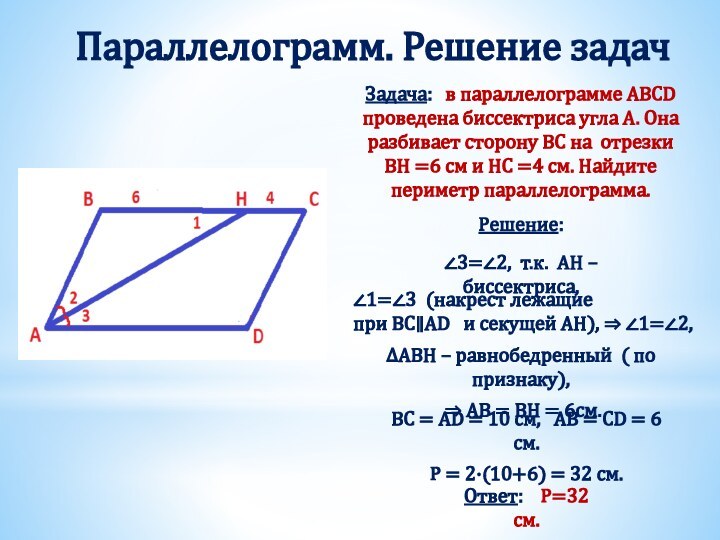
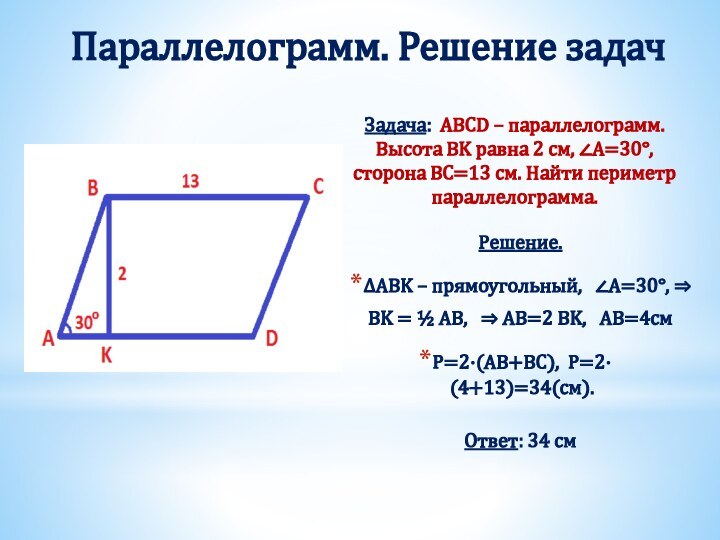
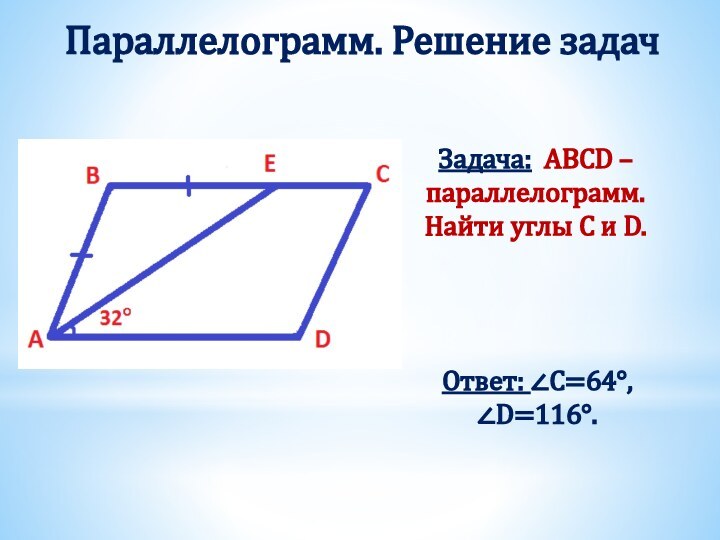
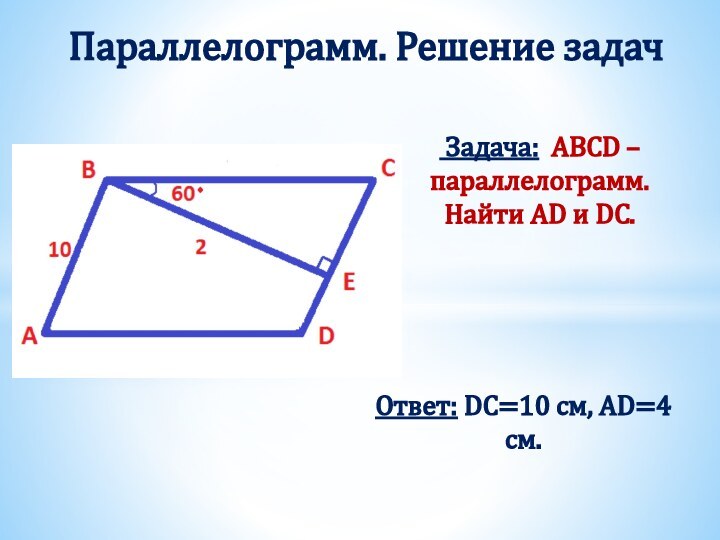
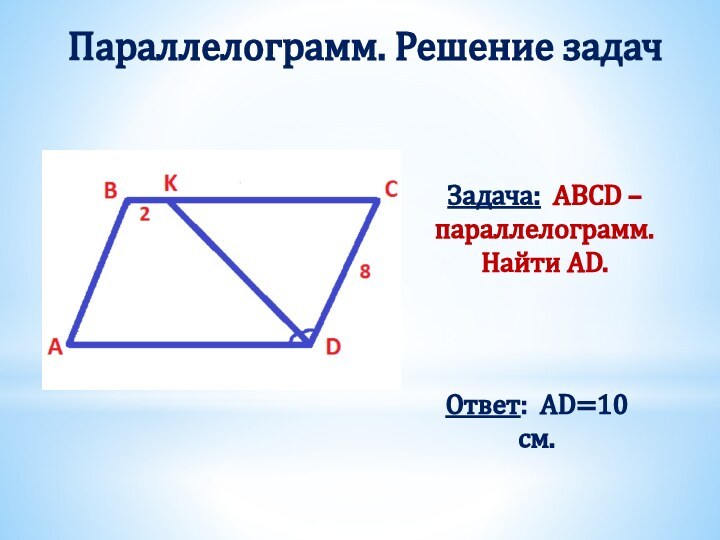
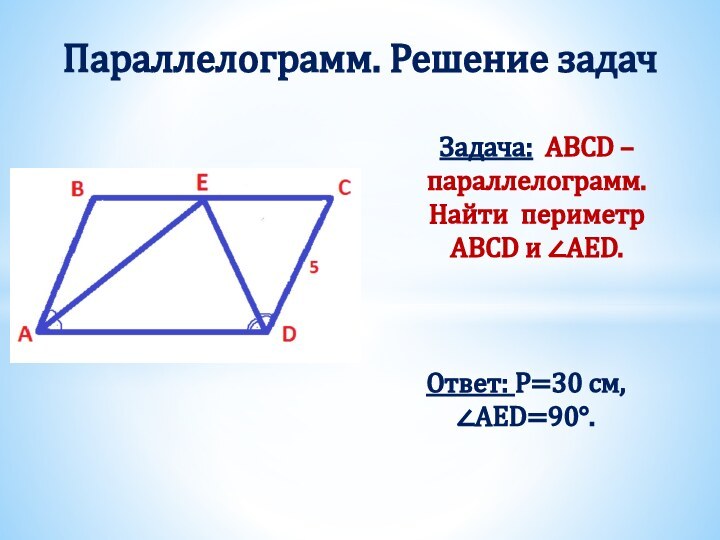
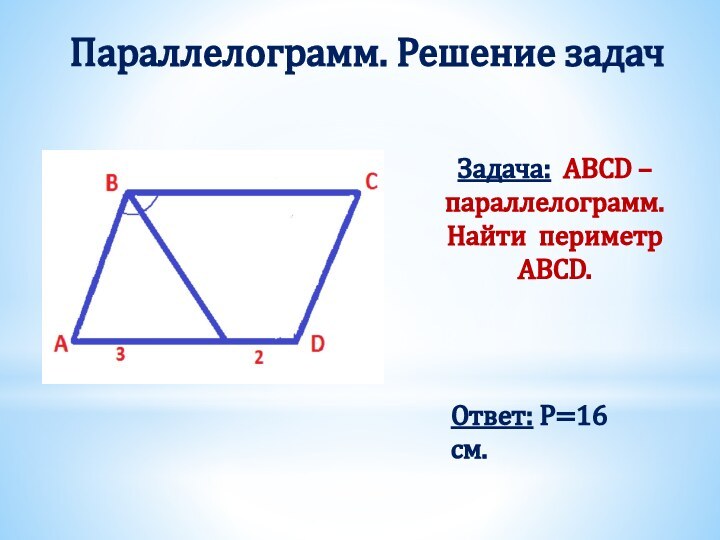
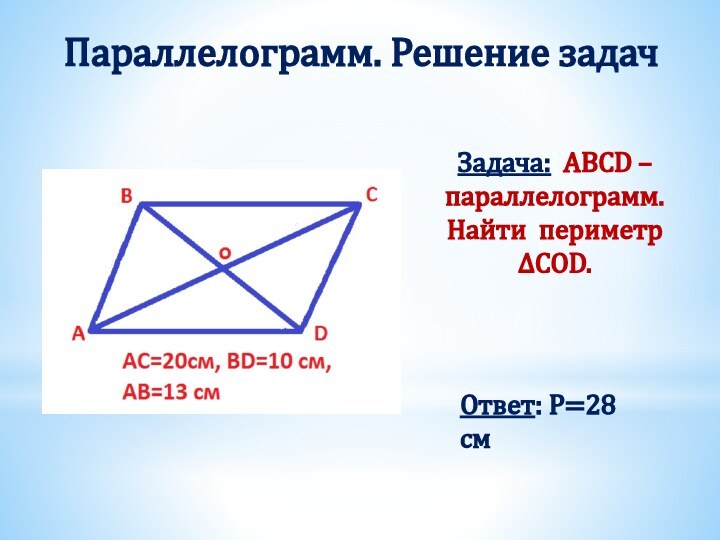
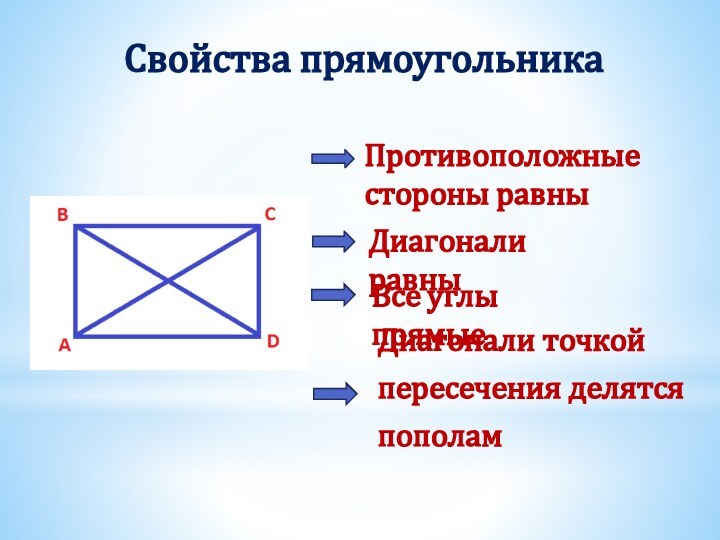
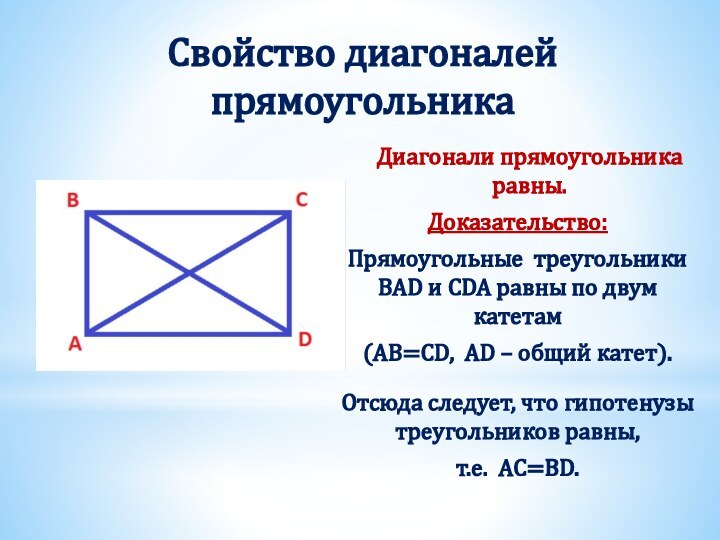
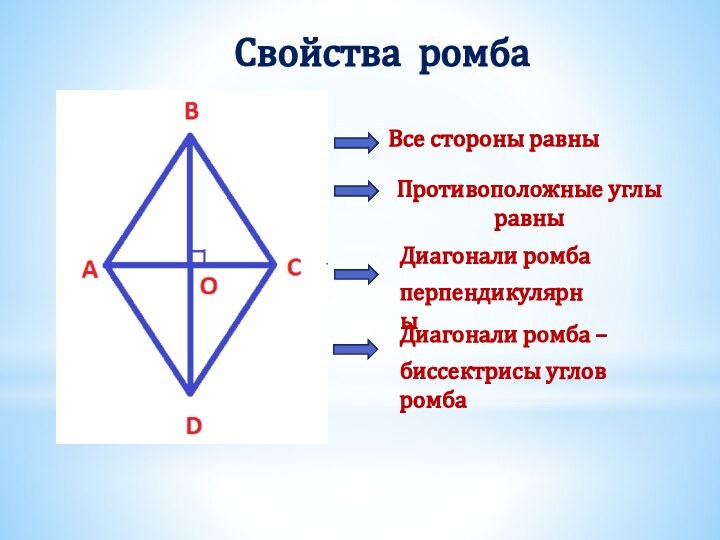
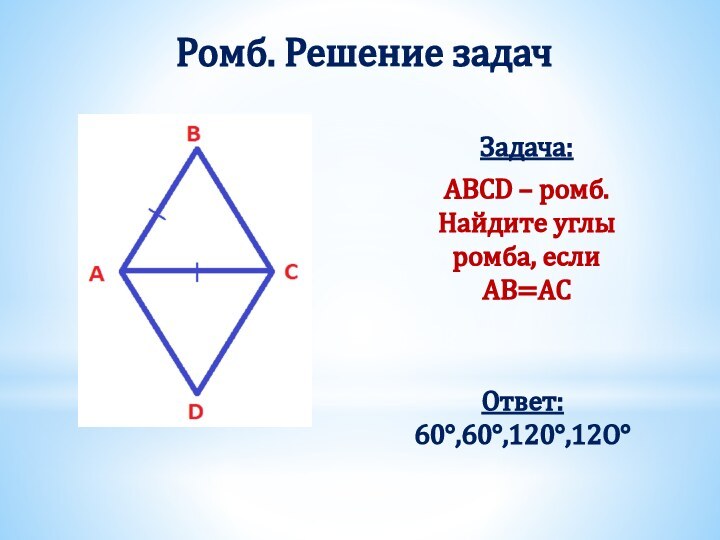
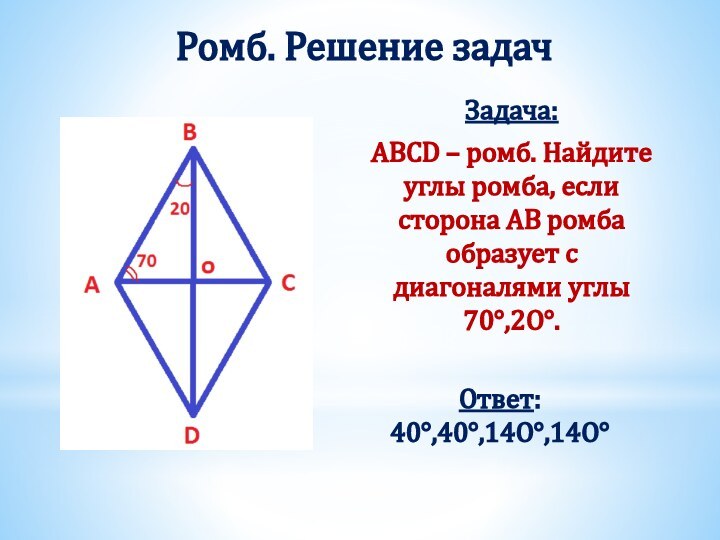
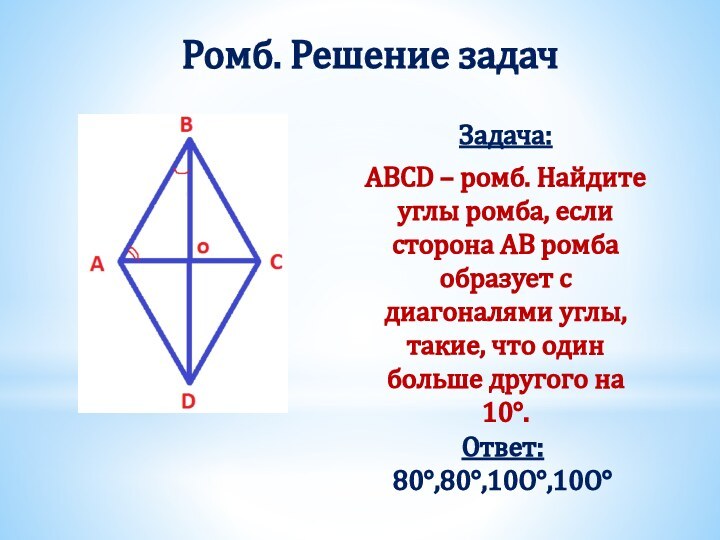
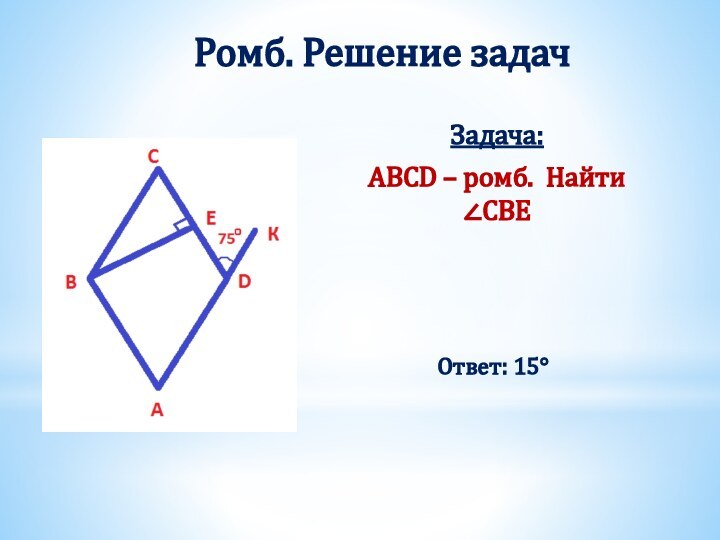
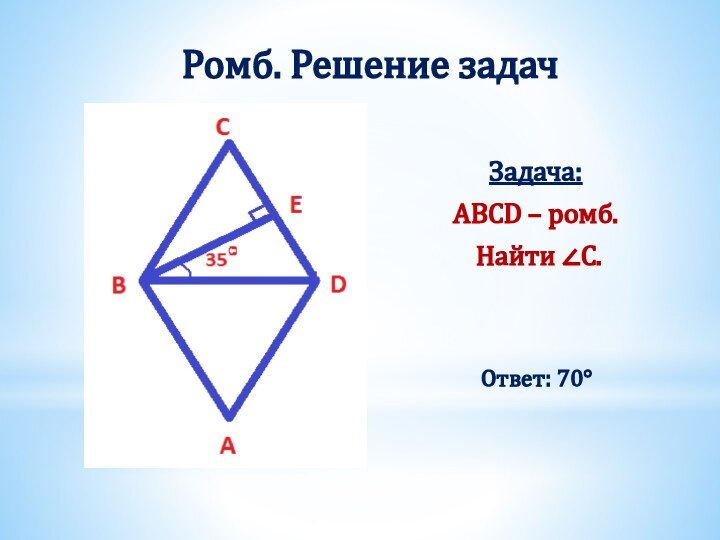
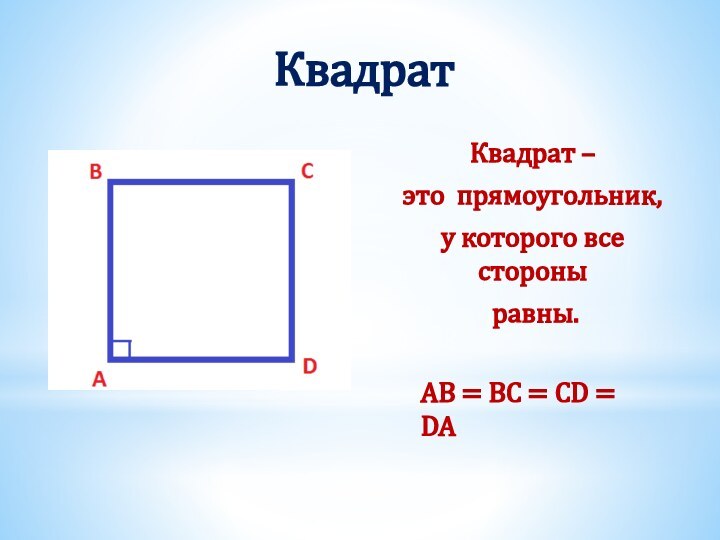
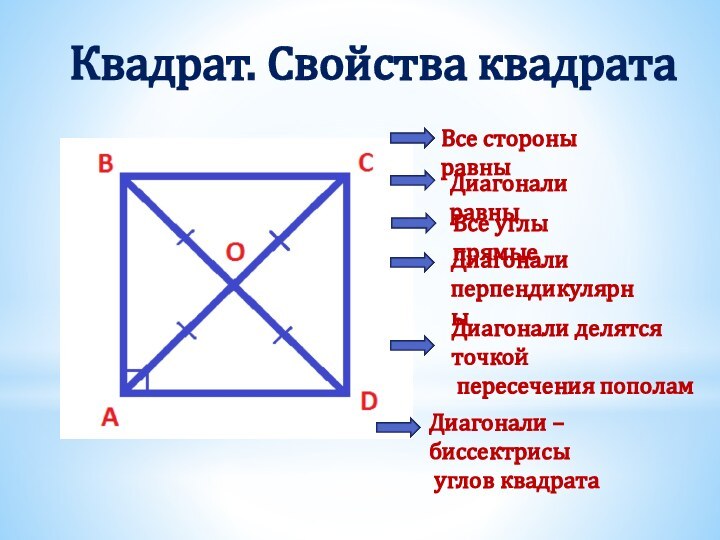
Получили два треугольника АВD и СDB.
Они равны, т.к.
BD – общая сторона,
∠ABD = ∠CDB (накрест лежащие при AB ∥ CD и секущей BD),
∠ADB = ∠DBC (накрест лежащие при BС ∥ AD и секущей BD).
Из равенства треугольников следует равенство соответствующих сторон, т.е. AB =CD , BC = AD