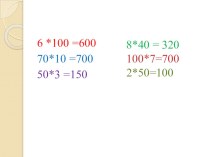30 = 0
имеет корни х1 = 10, х2
= 3; сумма
его корней х1 + х2 = 13, а их
произведение х1х2 = 30.
Отметим, что теорема Виета
справедлива и в случае, когда
квадратное уравнение имеет два
равных корня: х1 = х2 = - р/2.
Например, уравнение
х2 – 6х + 9 = 0
имеет равные корни: х1=х2 = 3; их сумма х1 + х2 = 6,
произведение х1х2 = 9
Задача1.
Один из корней уравнения
x ² + p x - 12 = 0
равен Х1 = 4.
Найти коэффициент p и второй корень х2 , этого уравнения.
По теореме Виета
х1+х2 = - p ,
х1х2 = - 12,
Так как Х1 = 4, то 4 х2 = - 12,
откуда х2 = - 3,
p = - ( х1 + х2) = -(4 – 3) = -1
Ответ: 3, - 1.