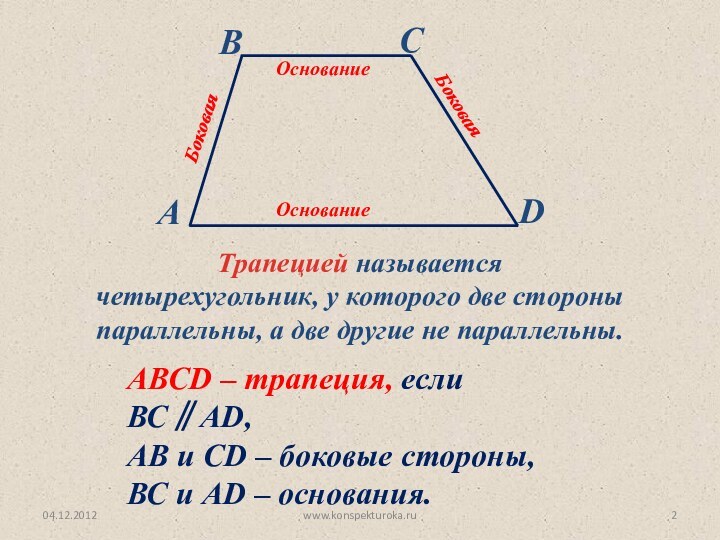
а две другие не параллельны.
АВСD – трапеция, если ВС∥AD,
АВ и СD – боковые стороны,
ВС и AD – основания.
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть

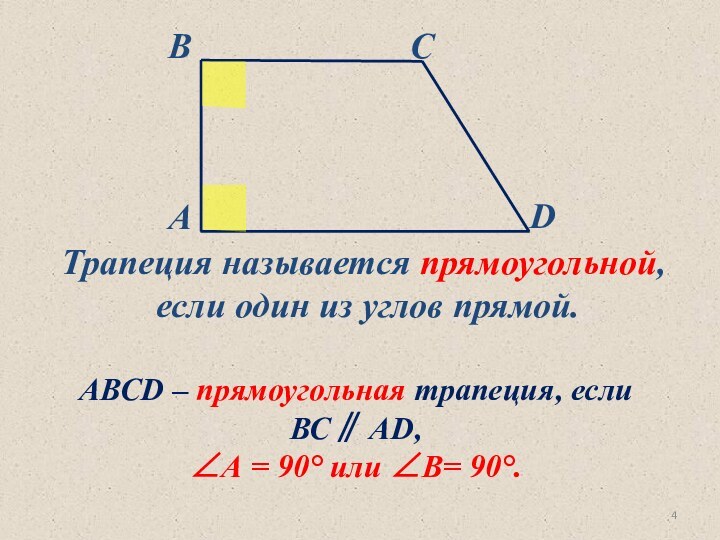
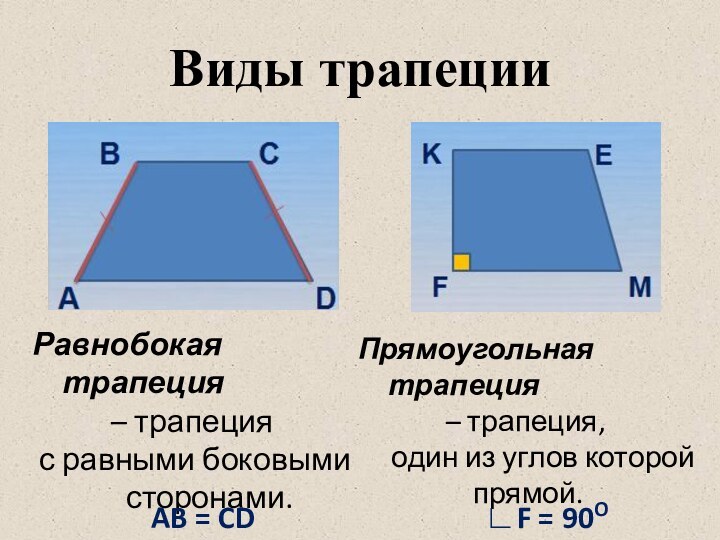

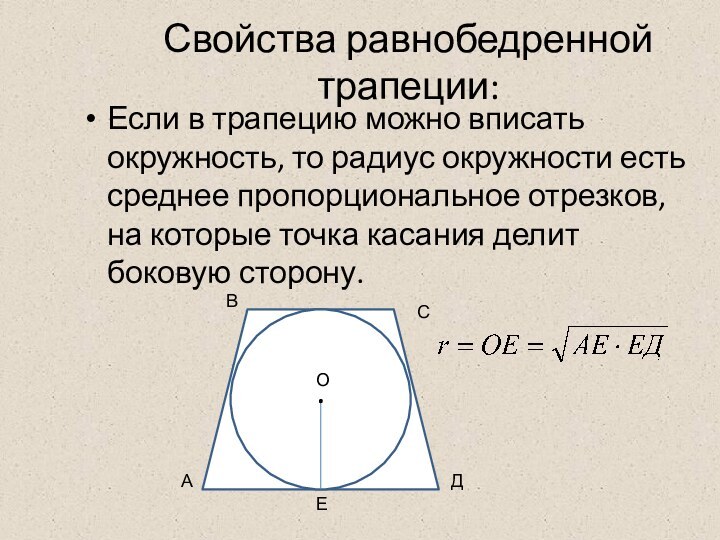
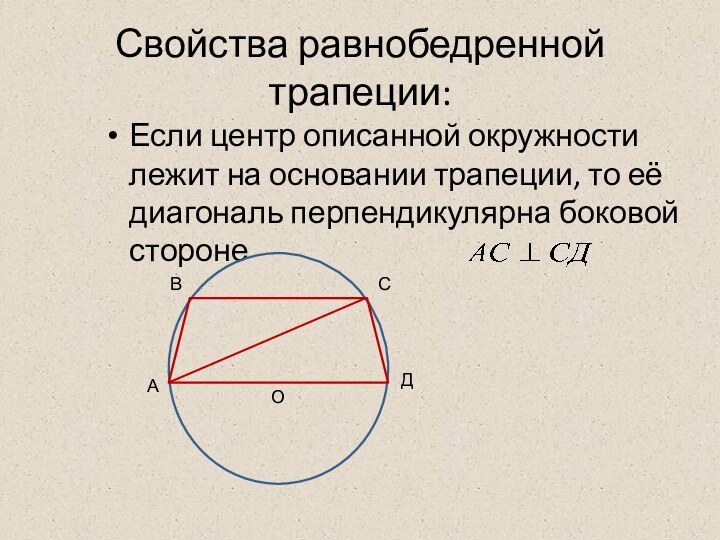
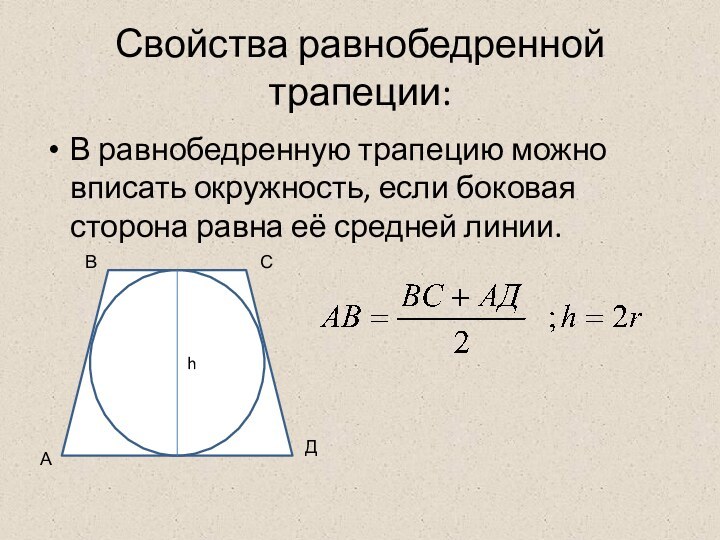

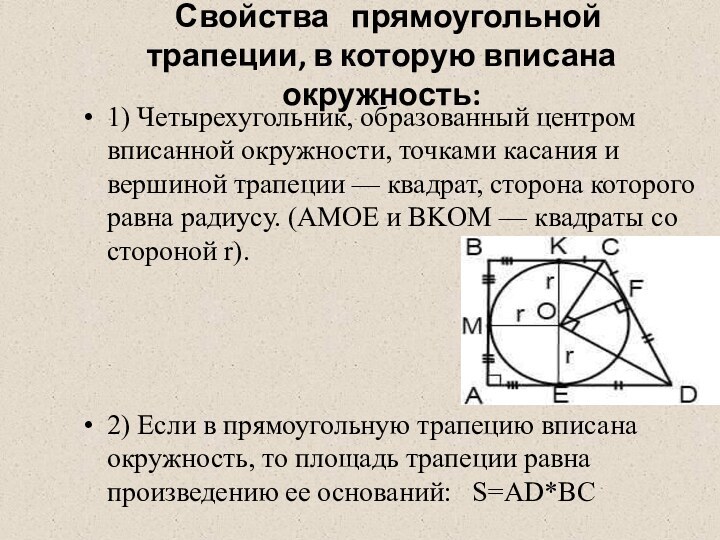
Прямоугольная трапеция
– трапеция,
один из углов которой
прямой.
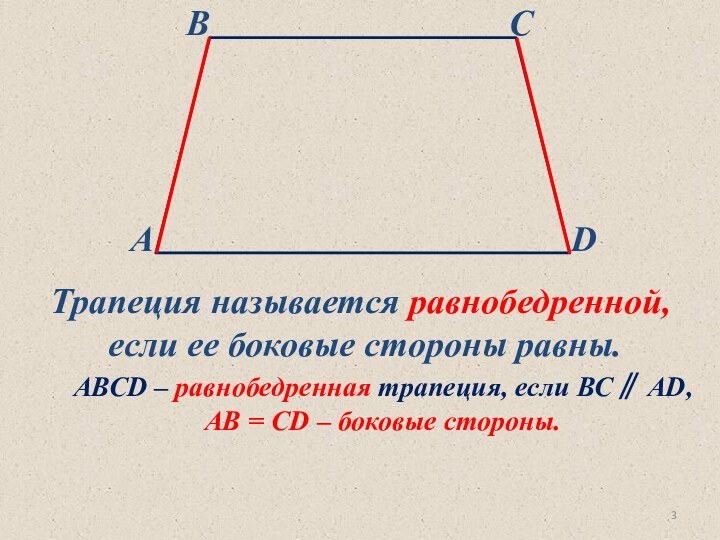
AB = CD
∟F = 90O
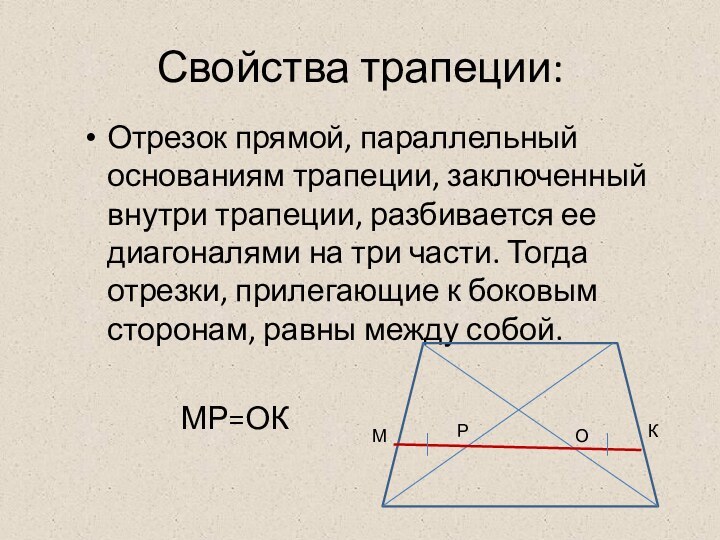
Р
М
О
К
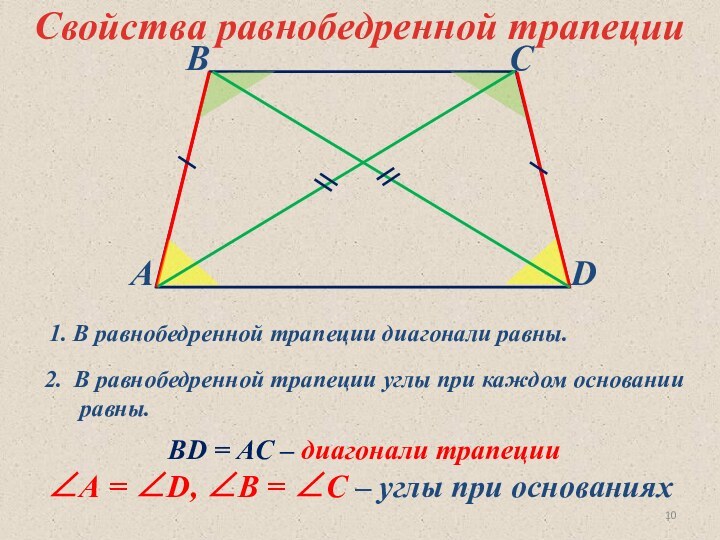
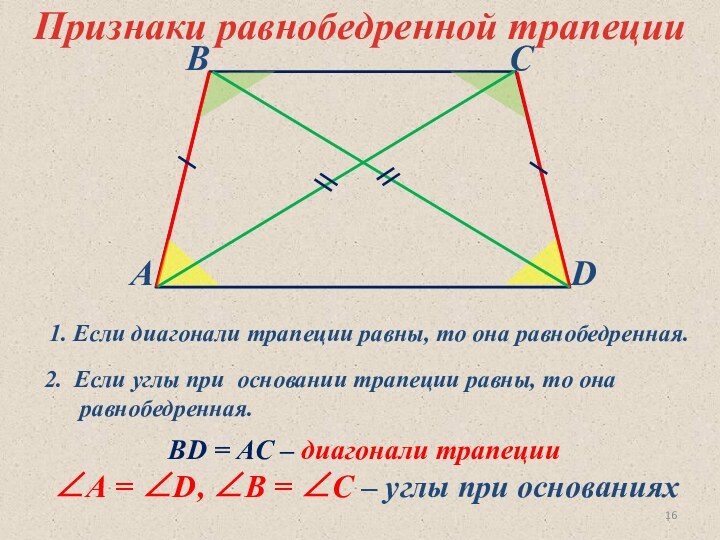
1. В равнобедренной трапеции диагонали равны.
О
О
1. Если диагонали трапеции равны, то она равнобедренная.
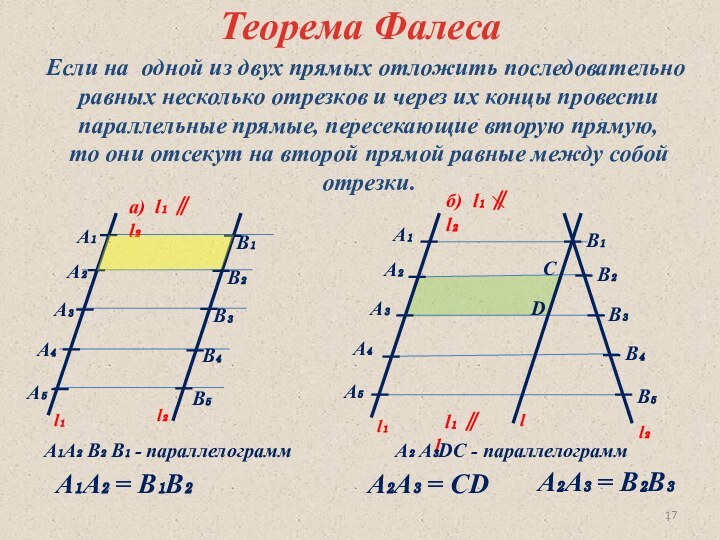
а) l₁ ∥ l₂
б) l₁ ∥ l₂
А₁А₂ = В₁В₂
l₁
l₁
l₂
l₂
А₁А₂ В₂ В₁ - параллелограмм
l₁ ∥ l
А₂ А₃DC - параллелограмм
А₂A₃ = CD
А₂A₃ = В₂B₃
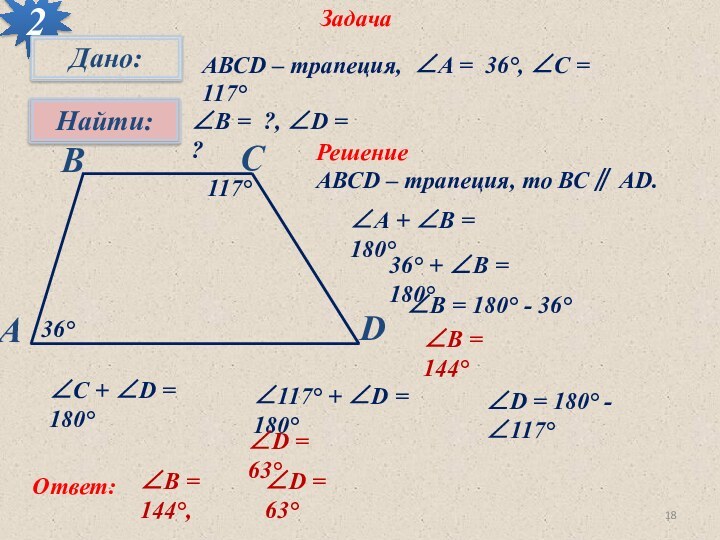
∠А + ∠В = 180°
36° + ∠В = 180°
∠В = 180° - 36°
∠В = 144°
∠С + ∠D = 180°
∠117° + ∠D = 180°
∠D = 180° - ∠117°
∠D = 63°
Ответ:
∠В = 144°,
∠D = 63°
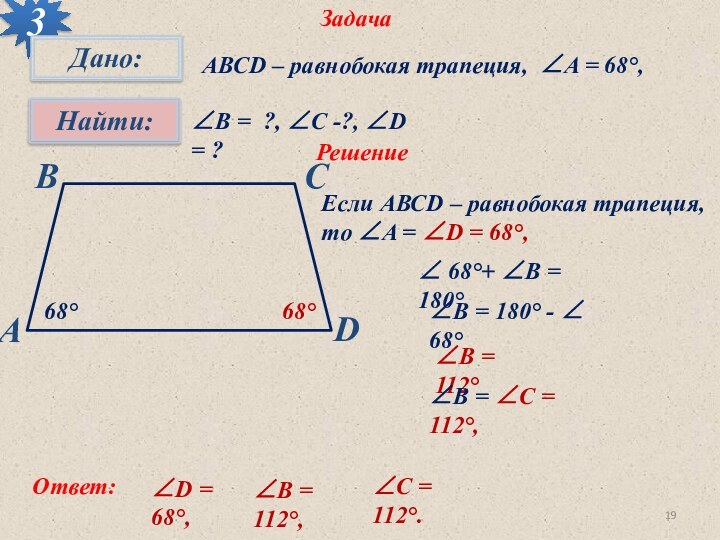
68°
68°
∠ 68°+ ∠В = 180°
∠В = 180° - ∠ 68°
∠В = 112°
∠В = ∠С = 112°,
Ответ: