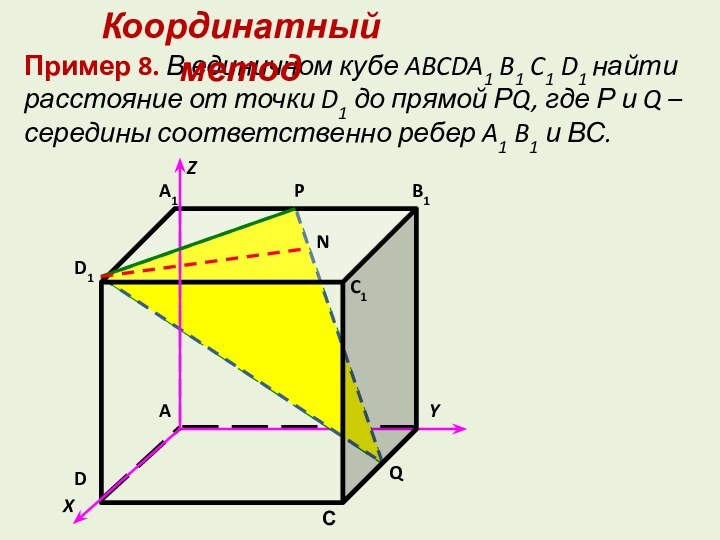
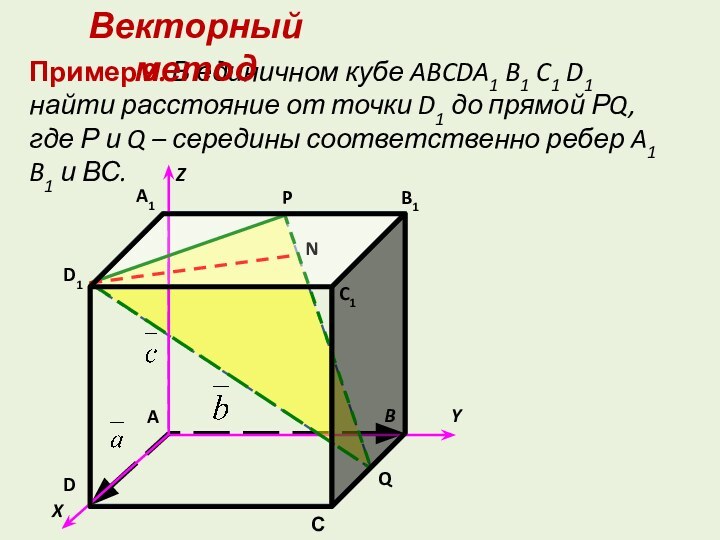
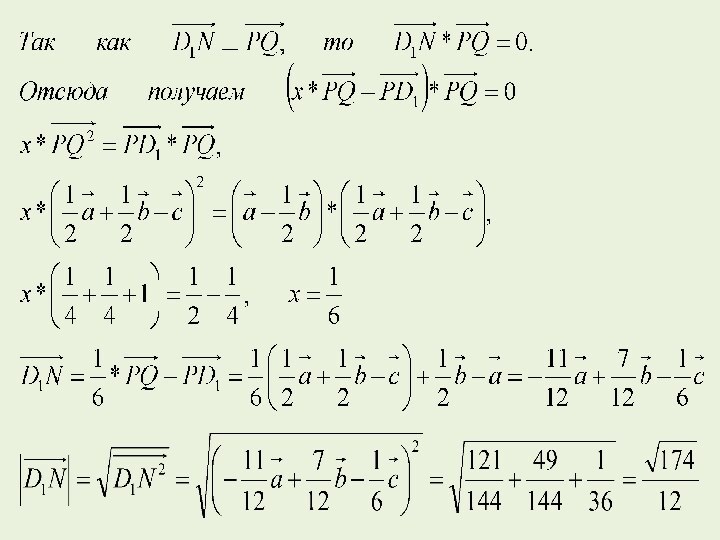точку, есть длина отрезка перпендикуляра, проведенного из этой точки
на прямую.Расстояние между двумя параллельными прямыми равно длине отрезка их общего перпендикуляра.
Расстояние между двумя параллельными прямыми равно расстоянию от любой точки одной из этих прямых до другой прямой.
1.2. Расстояние от точки до прямой