- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Числовые характеристики (параметры) распределений случайных величин
Содержание
- 2. литература
- 3. Математическое ожидание: центр распределения Дискретные распределенияНепрерывные распределения
- 5. Виды параметровМоментыначальныецентральныеПараметры сдвига математическое ожиданиемедианамодаПараметры формы дисперсияасимметрия эксцесс
- 6. Моменты
- 7. Связь между центральными и начальными моментамиПрименим формулу бинома Ньютона
- 8. Возьмем мат. ожидание от левой и правой
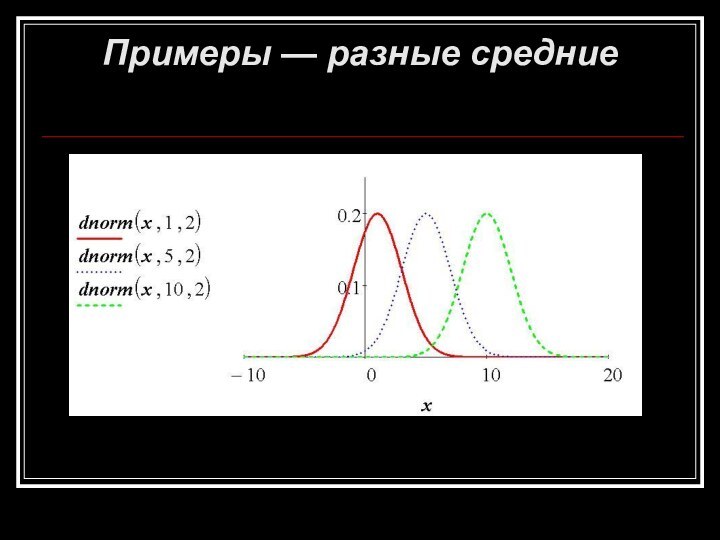
- 9. Примеры — разные средние
- 10. МодаЗначение Mo непрерывной случайной величины, при котором
- 11. Медиана Значение случайной величины x = Med,
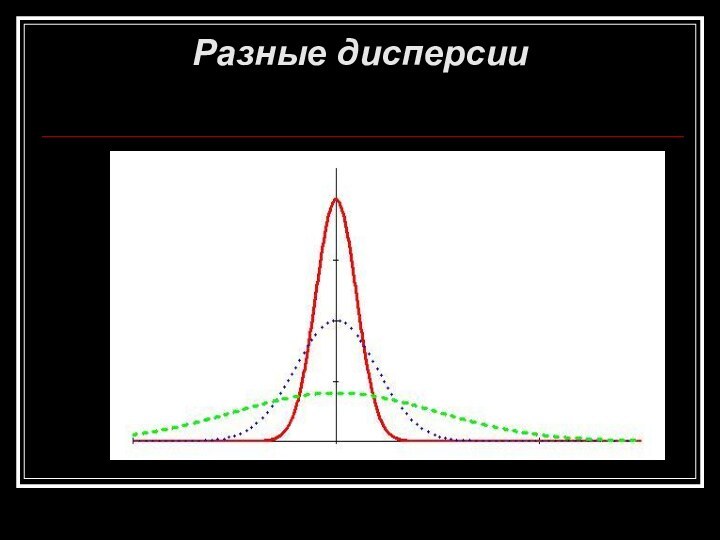
- 12. Параметры формы (масштаба)Дисперсия Dx и среднеквадратичное отклонение σ2Дискретные СВНепрерывные СВ
- 13. Разные дисперсии
- 14. Свойства дисперсии
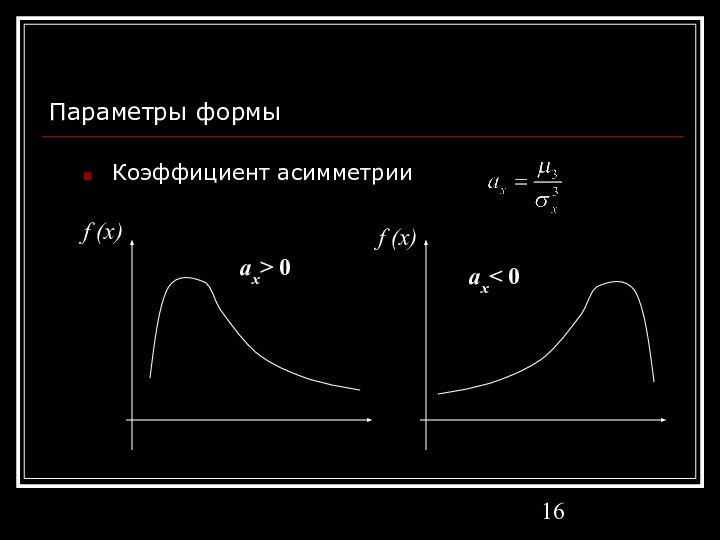
- 16. Параметры формы Коэффициент асимметрии
- 17. Параметры формыЭксцесс
- 18. Основные распределения и их свойства
- 19. Вырожденное распределение(Распределение константы)Распределение Бернулли (Распределение индикатора события)
- 20. Скачать презентацию
- 21. Похожие презентации
литература
Слайд 3
Математическое ожидание:
центр распределения
Дискретные распределения
Непрерывные
распределения
Слайд 5
Виды параметров
Моменты
начальные
центральные
Параметры сдвига
математическое ожидание
медиана
мода
Параметры формы
дисперсия
асимметрия
эксцесс
Слайд 8 Возьмем мат. ожидание от левой и правой частей
этого выражения и получим выражение, связывающее центральные и начальные
моменты
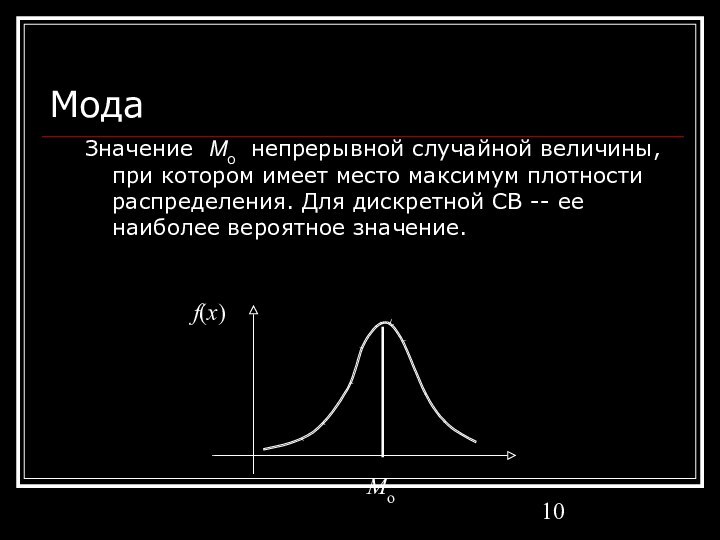
Слайд 10
Мода
Значение Mo непрерывной случайной величины, при котором имеет
место максимум плотности распределения. Для дискретной СВ -- ее
наиболее вероятное значение.
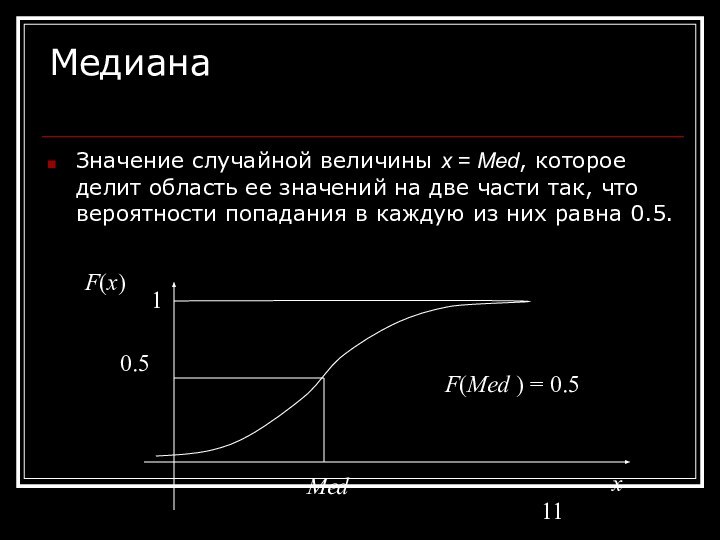
Слайд 11
Медиана
Значение случайной величины x = Med, которое делит
область ее значений на две части так, что вероятности
попадания в каждую из них равна 0.5.Med
F(Med ) = 0.5
Слайд 12
Параметры формы (масштаба)
Дисперсия Dx и среднеквадратичное отклонение σ2
Дискретные
СВ
Непрерывные СВ
Слайд 19
Вырожденное распределение
(Распределение константы)
Распределение Бернулли
(Распределение индикатора события)
