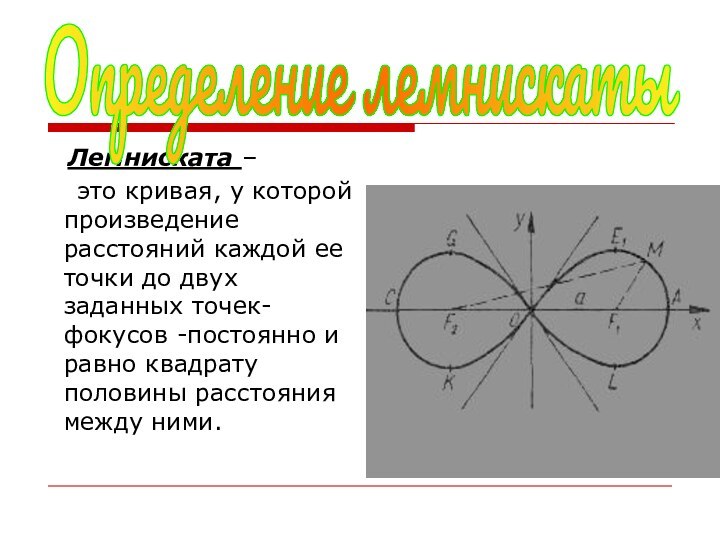
лемнискаты.
5.Уравнение лемнискаты в полярной системе координат.
6.Исследование уравнения лемнискаты.
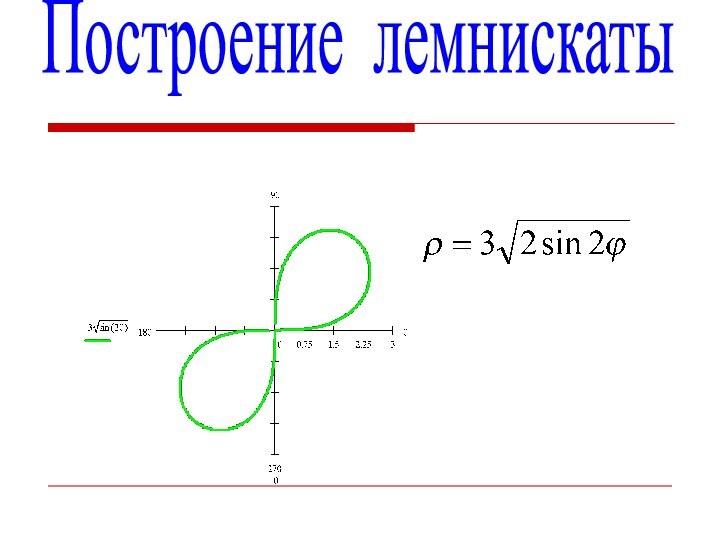
7.Построение лемнискаты.
8.
Применение лемнискаты.9.Краткая историческая справка.