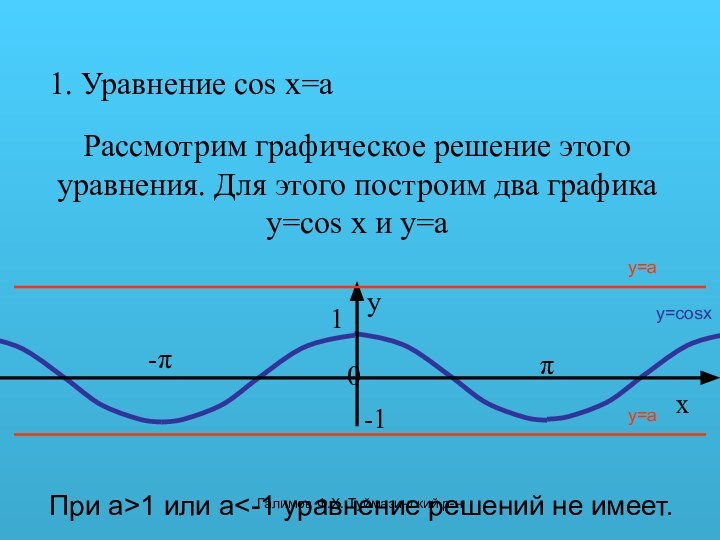
решение этого уравнения. Для этого построим два графика y=cos
x и y=ay=cosx
y=a
При а>1 или a<-1 уравнение решений не имеет.
y=a
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть
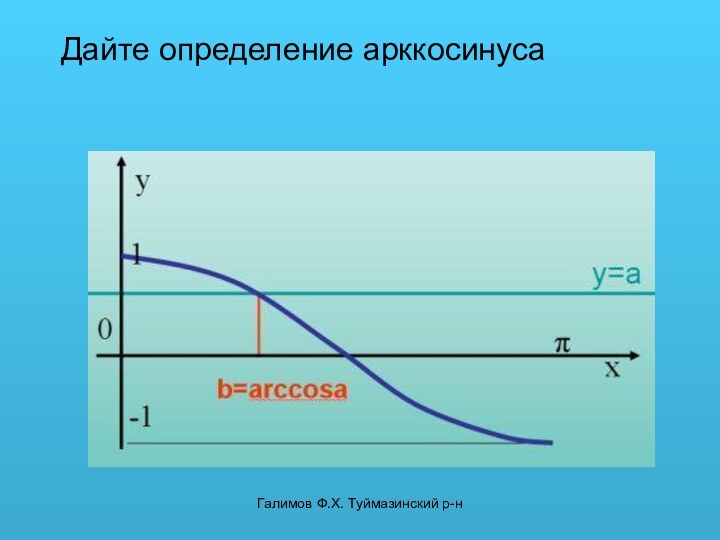
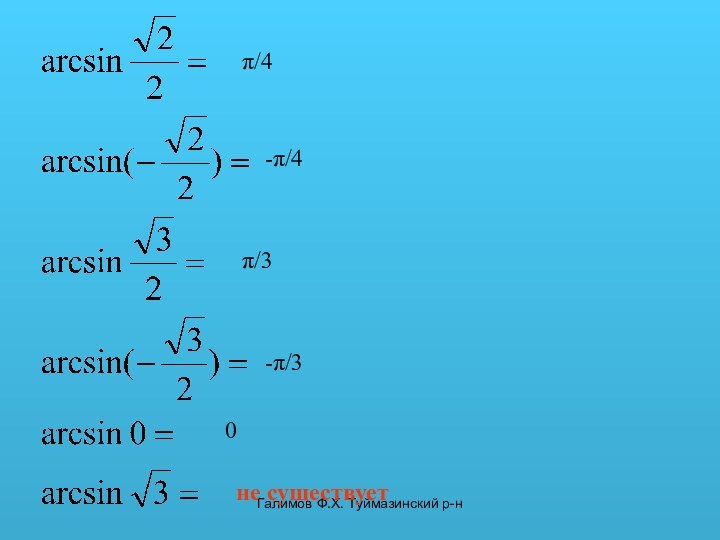




![Дайте определение арксинуса Галимов Ф.Х. Туймазинский р-нy=ay=aПри aЄ[-1;1] уравнение cos x=a имеет бесконечное множество решений.Мы](/img/tmb/14/1355114/81345f05efd72e5f8dbadd333ff4b7dd-720x.jpg)
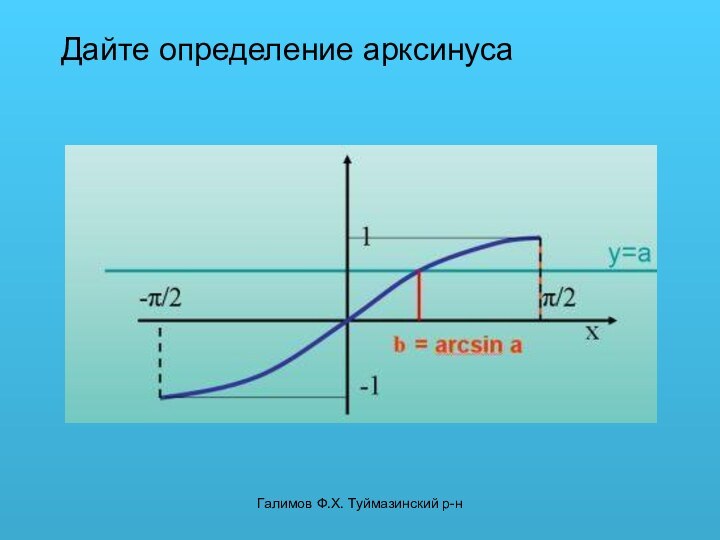
![Дайте определение арксинуса Галимов Ф.Х. Туймазинский р-нy=aПри aЄ[-1;1] уравнение sin x=a имеет бесконечное множество решений.Мы](/img/tmb/14/1355114/b00b2221e8c8947cd837b735664d875f-720x.jpg)








y=cosx
y=a
При а>1 или a<-1 уравнение решений не имеет.
y=a
x1=arccos a
Другие решения выразим через это решение.
x2=-arccos a
x3=arccos a-2π
-2π
+2π
x4=-arccos a+2π
Функция y=cos x имеет период 2π, поэтому остальные решения отличаются от х1 и х2 на 2πn, где nЄZ.
Таким образом все решения уравнения cos x=a записываются в виде
x=±arccos a+2πn, nЄZ
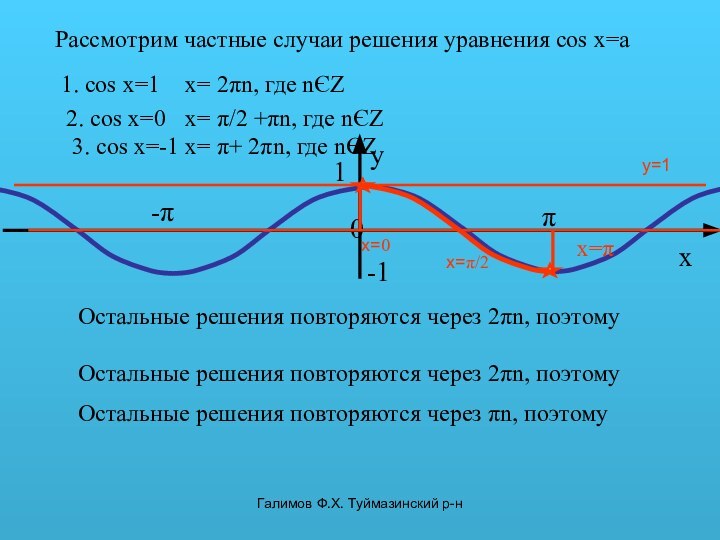
2. cos x=0
x=0
Остальные решения повторяются через πn, поэтому
x= π/2 +πn, где nЄZ
3. cos x=-1
Остальные решения повторяются через 2πn, поэтому
x= π+ 2πn, где nЄZ
x=π
y=a
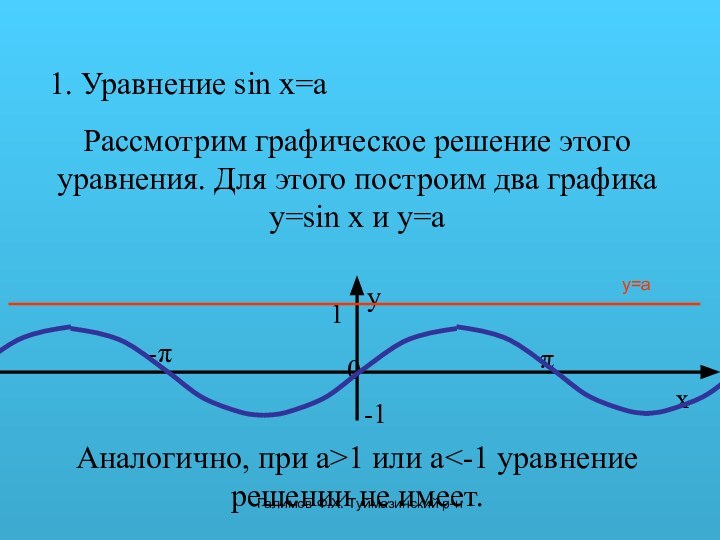
Аналогично, при a>1 или a<-1 уравнение решении не имеет.
x1=arcsin a
Другие решения выразим через это решение.
x2=π-arcsin a
Так-как функция y=sin x имеет период 2π, остальные решения отличаются от этих двух на 2πn, где nЄZ.
Получаем две группы решении
x1=arcsin a+ 2πn,
x2= π -arcsin a+ 2πn, где nЄZ,
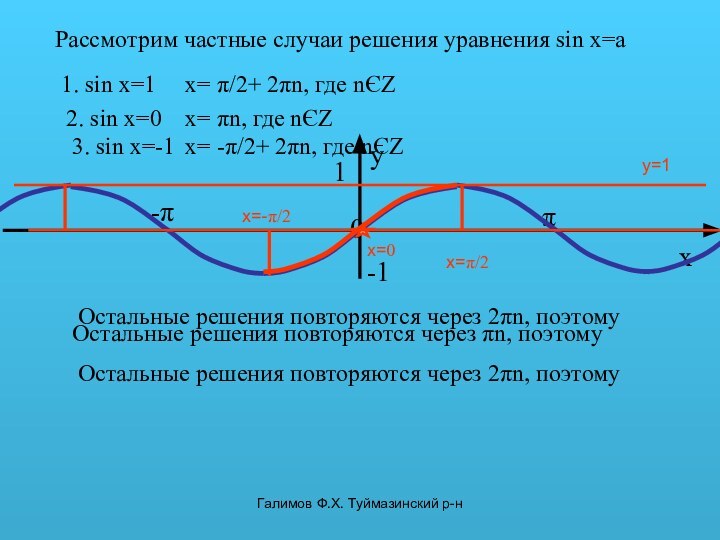
2. sin x=0
x=0
Остальные решения повторяются через πn, поэтому
x= πn, где nЄZ
3. sin x=-1
Остальные решения повторяются через 2πn, поэтому
x= -π/2+ 2πn, где nЄZ
x=-π/2