- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему по математике на тему Золотое сечение
Содержание
- 2. «…Геометрия владеет двумя сокровищами – теоремой Пифагора
- 3. Цель работы –расширить свой кругозор, способствовать развитию
- 4. Вы, наверное, обращали свое внимание,
- 5. Людей с давних времён волновал вопрос, подчиняются
- 6. Что же такое золотое сечение? Его можно
- 7. Термин золотое сечение ввёл в XVI веке
- 8. Деление отрезка в золотом отношении● ● A
- 9. Золотым называется такой равнобедренный треугольник, основание и боковая сторона которого находятся в золотом отношении.Золотой треугольник
- 10. Золотой прямоугольникПрямоугольник, стороны которого находятся в золотом
- 11. Золотая спираль
- 12. Золотое сечение и золотая спираль в природе
- 13. Золотое сечение и золотая спираль в природе
- 14. Парфенон
- 15. ПентаграммаПентаграмма представляет собой вместилище золотых пропорций! Интересно,
- 16. Закон угловВ 1850 г. немецкий учёный
- 17. Деление отрезка в золотом отношении
- 18. Скачать презентацию
- 19. Похожие презентации
«…Геометрия владеет двумя сокровищами – теоремой Пифагора и золотым сечением, и если первое из них можно сравнить с мерой золота, то второе – с драгоценным камнем…» ,

















Слайд 3
Цель работы –
расширить свой кругозор, способствовать развитию познавательного
интереса;
показать обще интеллектуальное значение математики;
способствовать познанию законов красоты и
гармонии окружающего мира.Слайд 4 Вы, наверное, обращали свое внимание, что мы неодинаково
относимся к предметам и явлениям окружающей действительности. Беспорядочность, бесформенность,
несоразмерность воспринимают нами как нечто безобразное и производят отталкивающее впечатление. А предметы и явления, которые свойственная мера, целесообразность и гармония, воспринимаются как красивые и вызывают у нас чувство восхищения, радость, поднимают настроениеСлайд 5 Людей с давних времён волновал вопрос, подчиняются ли
такие неуловимые вещи как красота и гармония, каким-либо математическим
расчётам.Можно ли «проверить алгеброй гармонию?» – как сказал А.С. Пушкин.
Конечно, все законы красоты невозможно вместить в несколько формул, но, изучая математику, мы можем открыть некоторые слагаемые прекрасного.
Слайд 6
Что же такое золотое сечение?
Его можно разделить
точкой С на две части бесконечным множеством способов, но
говорят что точка С производит золотое сечение отрезка АВ, если выполняется пропорция: длина меньшего отрезка так относится к длине большего, как больший отрезок относится к длине всего отрезка, т.е.Рассмотрим отрезок АВ.
А
В
С
Слайд 7 Термин золотое сечение ввёл в XVI веке великий
художник, учёный и изобретатель Леонардо да Винчи. В истории
утвердились три варианта названия: золотое сечение, золотая пропорция и третье - деление отрезка в среднем и крайнем отношениях. Кроме того, золотое сечение награждали эпитетами «божественное», «чудесное», «превосходнейшее», потому что-то, где оно присутствует, вызывает у нас ощущение красоты и гармонии.
Слайд 8
Деление отрезка в золотом отношении
●
●
A
C
B
E
D
Дано: отрезок АВ.
Построить:
золотое сечение отрезка
АВ, т.е. точку С так, чтобы Построение
l
Построим прямоугольный треугольник, у которого один катет в два раза больше другого. Для этого восстановим в точке В перпендикуляр к прямой АВ и на нём отложим отрезок BD = 0,5 AB.
Далее, соединив точки А и D, отложим отрезок DЕ = ВD, и, наконец, АС = АЕ. Точка С является искомой, она производит золотое сечение отрезка АВ.
●
Слайд 9 Золотым называется такой равнобедренный треугольник, основание и боковая
сторона которого находятся в золотом отношении.
Золотой треугольник
Слайд 10
Золотой прямоугольник
Прямоугольник, стороны которого находятся в золотом отношении,
т.е. отношение ширины к длине даёт число φ, называется
золотым прямоугольником.
Слайд 15
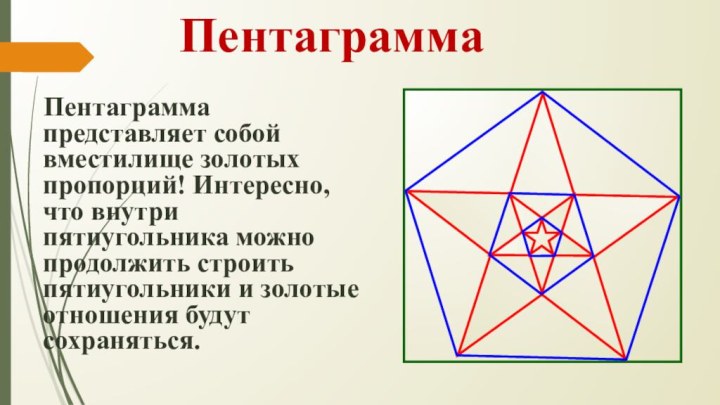
Пентаграмма
Пентаграмма представляет собой вместилище золотых пропорций! Интересно, что
внутри пятиугольника можно продолжить строить пятиугольники и золотые отношения
будут сохраняться.
Слайд 16
Закон углов
В 1850 г. немецкий учёный
А. Цейзинг открыл так
называемый закон углов, согласно которому средняя величина углового отклонения ветки растения равна примерно 138 градусов.
Слайд 17
Деление отрезка в золотом отношении
На отрезке АВ построим квадрат АВСD. Найдём точку
Y, делящую АВ в среднем отношении.Соединим точку Е (середину АС) с точкой В. На продолжении стороны СА квадрата отложим отрезок ЕJ = ВЕ. На отрезке AJ построим квадрат AJHY.
Продолжение стороны HJ до пересечения с CD в точке К делит квадрат ABCD на два прямоугольника AYKC и YBDK.
Существует чисто геометрическое доказательство, что прямоугольник YBDK равновелик квадрату AJHY.
«Начала Евклида»
Геометрическое решение