Презентация на тему Дискретные структуры. Теория множеств. Бинарные отношения. Отношение эквивалентности

их задания для применения в задачах компьютерной инженерии
Содержание:

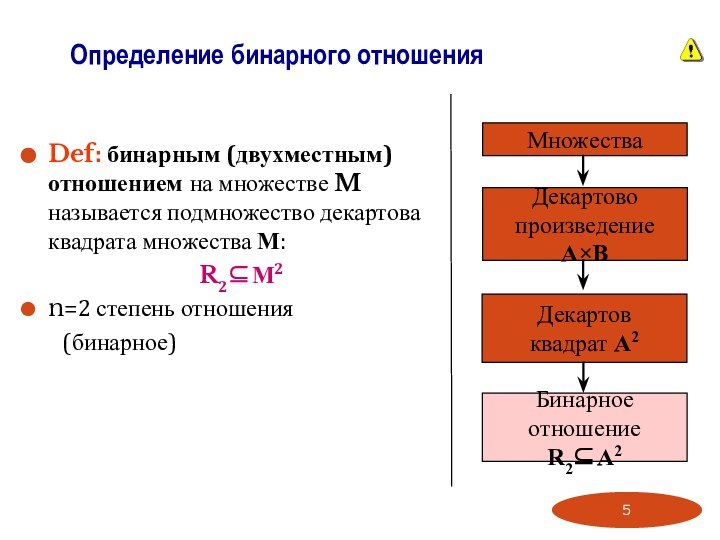
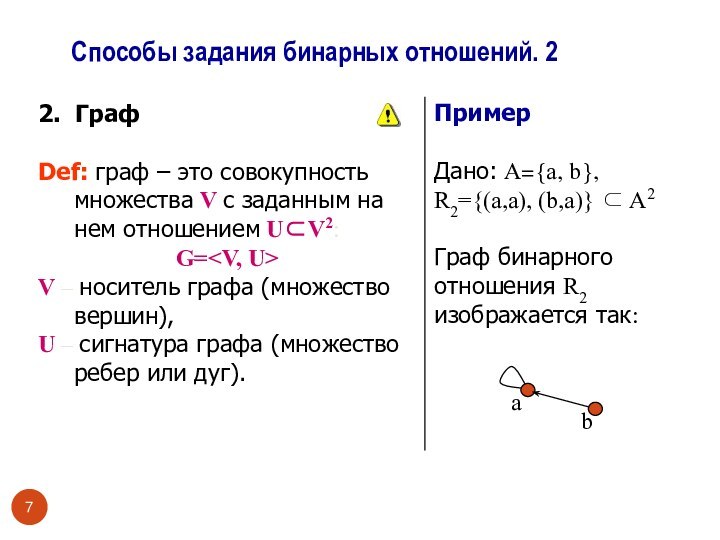
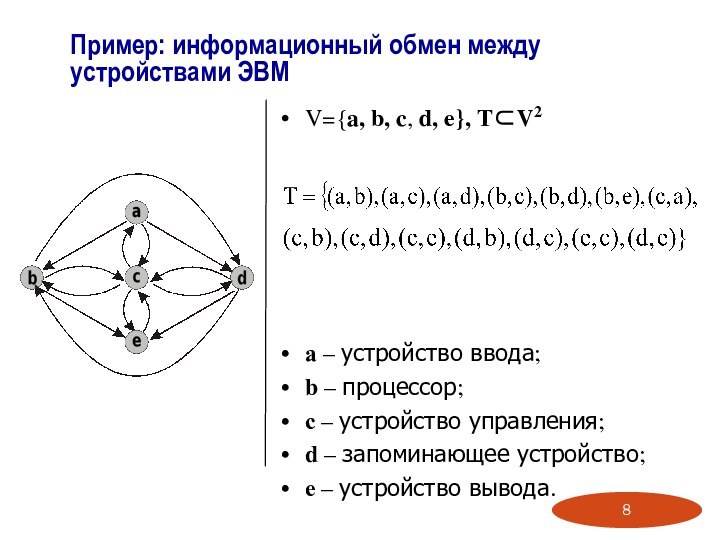
Определение бинарного отношения
Способы задания бинарных отношений
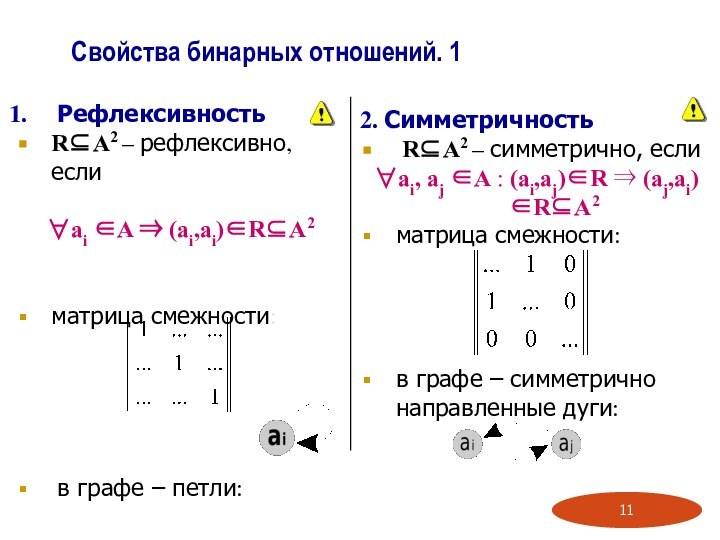
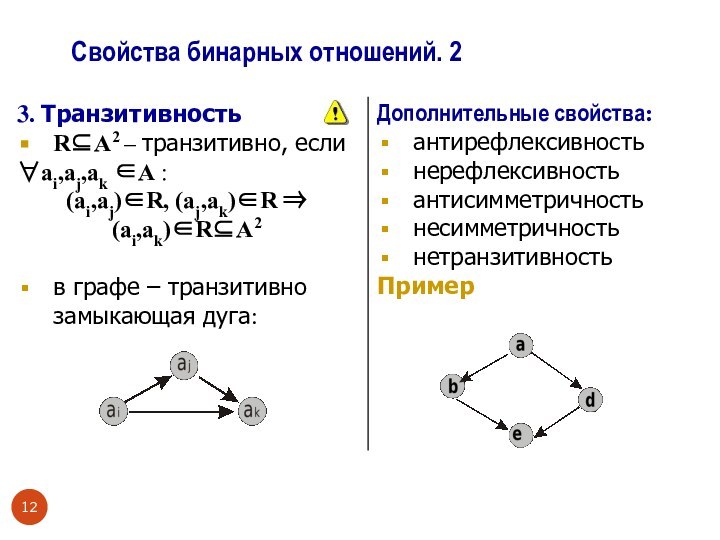
Свойства бинарных отношений
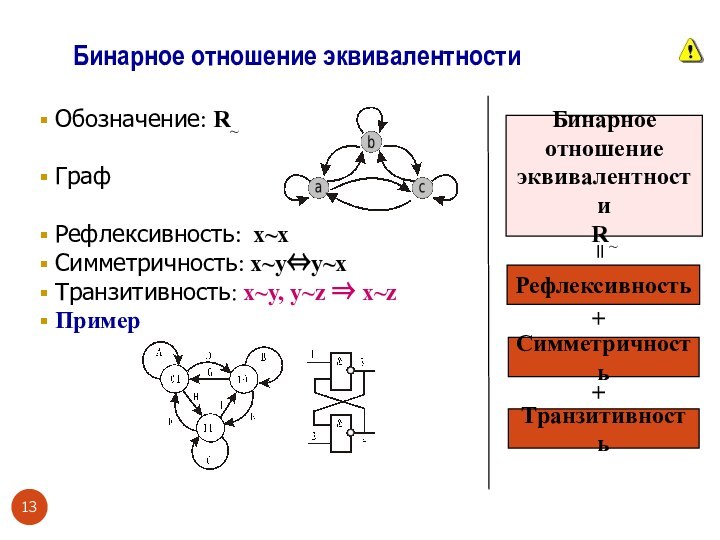
Бинарное отношение эквивалентности
Классы эквивалентности
Применение в задачах компьютерной инженерии

Тема: Бинарные отношения. Отношение эквивалентности

шк., 1986. 10-14 с.
Лавров И.А., Максимова Л.Л. Задачи

по теории множеств, математической логике и теории алгоритмов. М.: Наука. Главная редакция физико-математической литературы, 1984. 224 с.
Кузнецов О.П., Адельсон-Вельский Г.М. Дискретная математика для инженера. М.: Энергия, 1980. 344 с.
Богомолов А.М., Сперанский Д.В. Аналитические методы в задачах контроля и анализа дискретных устройств. Саратов: Изд-во Саратовкого ун-та, 1986. 240с.
Новиков Ф.А. Дискретная математика для программистов. С.-П., 2001. С. 4-24.
Хаханов В.І., Хаханова І.В., Кулак Е.М., Чумаченко С.В. Методичні вказівки до практичних занять з курсу “Дискретна математика”. Харків, ХНУРЕ. 2001. 12-16 с.

декартово произведение
декартова степень
отношение
Ключевые слова:
бинарное отношение
матрица

смежности
граф
фактор-множество
рефлексивность
симметричность
транзитвность
отношение эквивалентности

подмножество декартова квадрата множества М:
R2⊆М2
n=2 степень отношения
(бинарное)

Определение

бинарного отношения

смежности
бинарного отношения на
множестве А={а1, а2, а3, …, an} –
это

таблица размера n×n,
в которой элемент cij ,
определяется следующим образом:

Пример

Дано: А={а, b},
R2={(a,a), (b,a)} ⊂ A2

Матрица смежности
бинарного отношения
R2 представляется так:

это совокупность множества V с заданным на нем отношением

U⊂V2:
G=
V – носитель графа (множество вершин),
U – сигнатура графа (множество ребер или дуг).

Пример

Дано: А={а, b},
R2={(a,a), (b,a)} ⊂ A2

Граф бинарного
отношения R2
изображается так:

ввода;
b – процессор;
c – устройство управления;
d

– запоминающее устройство;
e – устройство вывода.

Пример: информационный обмен между устройствами ЭВМ

физико-математических наук
Член Национальной Академии наук США

Профессор Принстонского университета в США (с 1933)
Член Комиссии по атомной энергии США (с 1954)
Директор Бюро по проектиро-ванию ЭВМ (1945-1955).

радиуса элемента ai∈A :

O(ai)={ aj | (ai,aj)∈R⊆A2, aj∈A }

Def:

фактор-множество A/R
(или A|R) множества A по
отношению R⊆A2 есть
совокупность окрестностей
единичного радиуса

A/R = { O(ai) | ai∈A }

Пример

a b c d e
{b,c,d}{c,d,e}{a,b,d,e}{b,c,а}{c}

Верхняя строка – элементы множества A
Нижняя – совокупность окрестностей единичного радиуса элементов ai

смежности:





в графе – петли:
2. Симметричность
R⊆A2

– симметрично, если
∀ai, aj ∈A : (ai,aj)∈R ⇒ (aj,ai)∈R⊆A2
матрица смежности:




в графе – симметрично направленные дуги:

Свойства бинарных отношений. 1

(aj,ak)∈R ⇒
(ai,ak)∈R⊆A2

в графе – транзитивно замыкающая дуга:
Дополнительные

свойства:
антирефлексивность
нерефлексивность
антисимметричность
несимметричность
нетранзитивность
Пример

Свойства бинарных отношений. 2

Симметричность: x~y⇔y~x
Транзитивность: x~y, y~z ⇒ x~z
Пример

семейство непустых попарно непересекающихся подмножеств, объединение которых совпадает с

А
Свойства Г⊂В(А)
∀Ki∈A: Ki ≠∅
∀Ki, Kj ∈Г: Ki∩Kj = ∅

Пример
Для трехэлементного множества
A={a,b,c} разбиениями являются
Г1={ {a, b, c} }
Г2={ {a}, {b}, {c} }
Г3={ {a}, {b,c} }
Г4={ {b}, {a,c} }
Г5={ {c}, {a,b} }

задано отношение эквивалентности R~

Выберем элемент a1∈A и образуем

подмножество (класс) K1⊂A, состоящий из элемента а1 и всех элементов, эквивалентных ему:


Выберем элемент a2∈A, а2≠а1, и образуем подмножество (класс) K2⊂A, состоящий из элемента а2 и всех элементов, эквивалентных ему:


Таким образом, получаем систему классов, объединение которых совпадает с множеством А

образует разбиение
любые два элемента из одного класса эквивалентны

любые два элемента из разных классов не эквивалентны

Def: класс эквивалентности [à] элемента à
[a]={ x | x~a, x∈A }

Свойства классов эквивалентности:
a∈[a]
b∈[a]⇒[b]=[a]
[a]∩[b]=∅,
[a]∩[b]≠∅⇒ [a]=[b]

представить в блочно-диагональном виде, где каждая подматрица, состоящая из

единиц, соответствует классу эквивалентности

деталей, признаков моделируемого объекта. Отношение эквивалентности, с одной стороны,

отождествляет второстепенные, несущественные признаки и свойства, и, с другой – выделяет в качестве представителей классов эквивалентности основные свойства.
Понятия "отношение эквивалентности", "фактор-множество", "классы эквивалентности" используются при построении математической модели некоторой реально функционирующей сложной системы.
Модель есть некоторое фактор-множество элементов моделируемого объекта относительно некоторого отношения эквивалентности, заданного на исходной системе.

композиции элементов некоторого базисного множества, то вопрос о соотношении

модели и ее прообраза разрешается на основе информации об элементах, на которых вводится отношение эквивалентности - либо это сами элементы базисного множества, либо некоторые подмножества элементов, либо подмножества множества подмножеств элементов.