Презентация на тему Начертательная геометрия

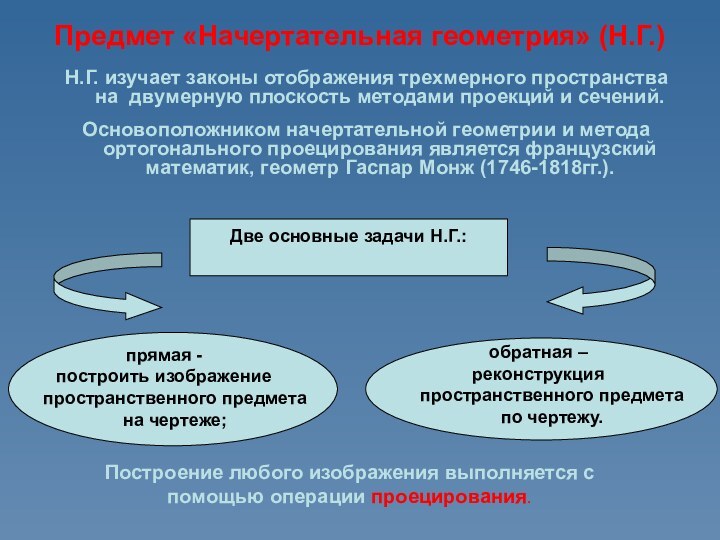
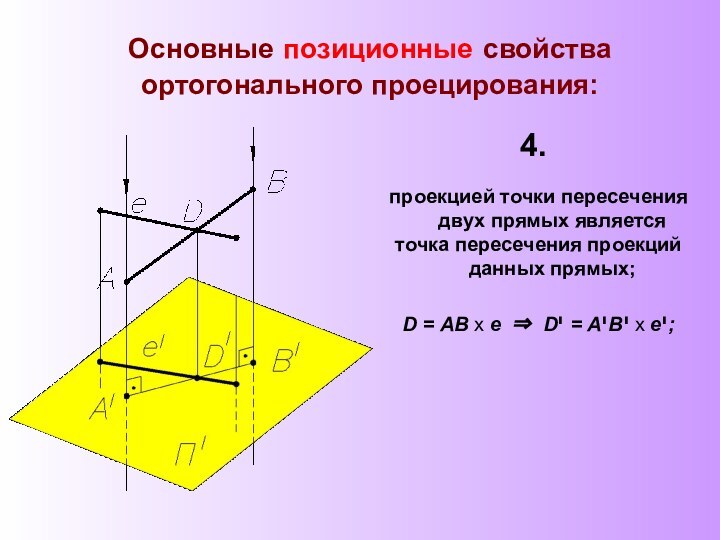
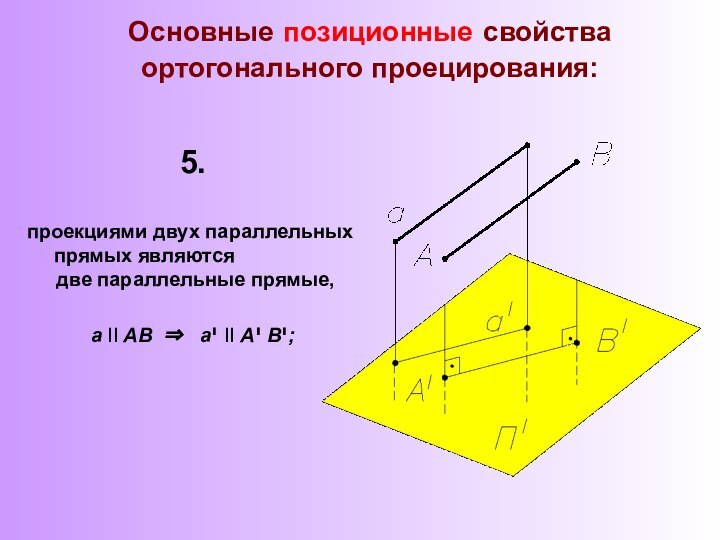
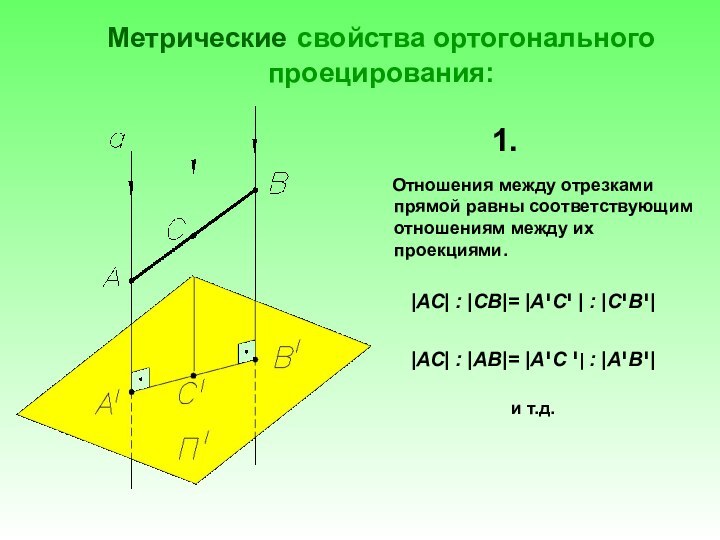
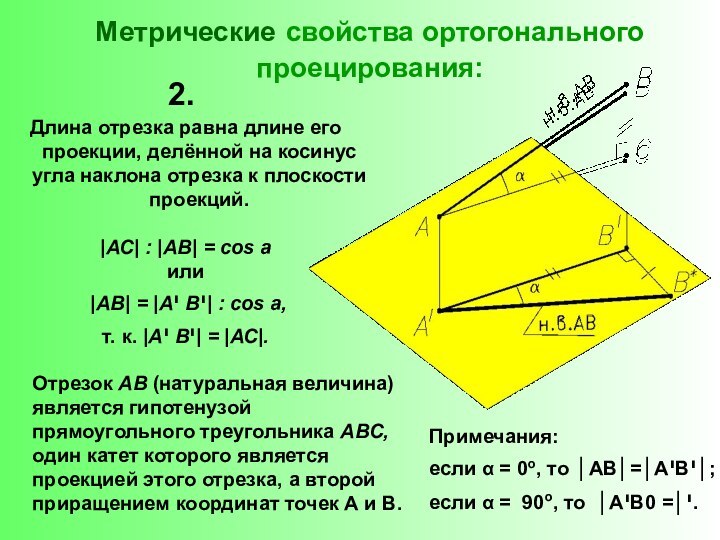
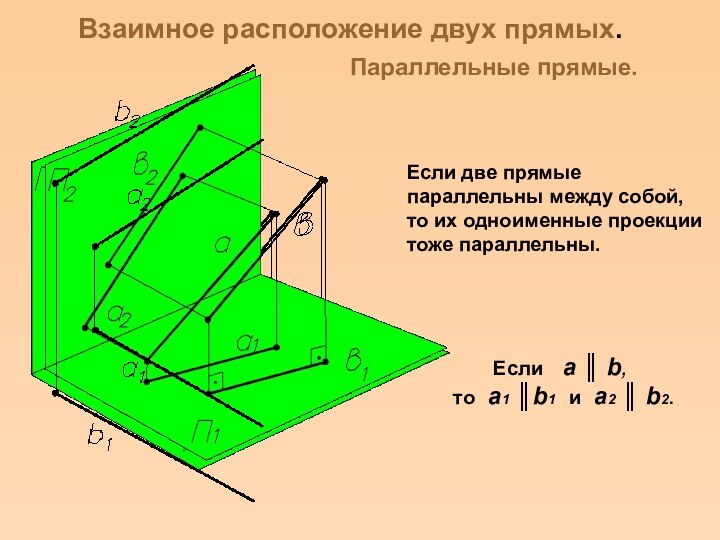
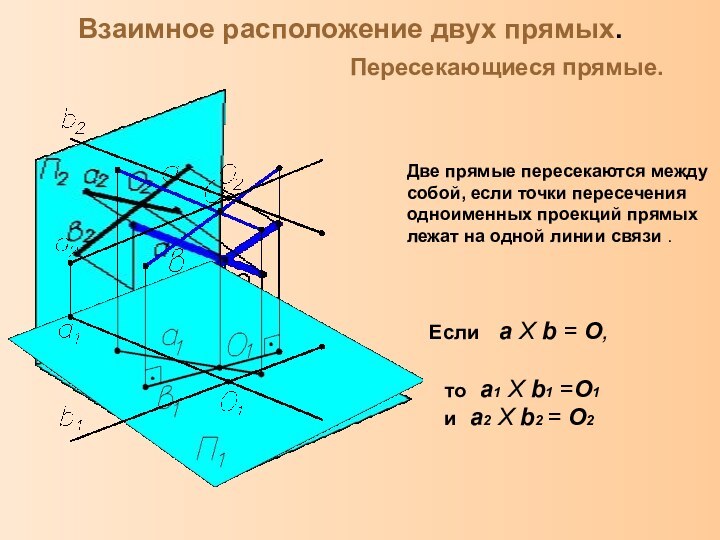
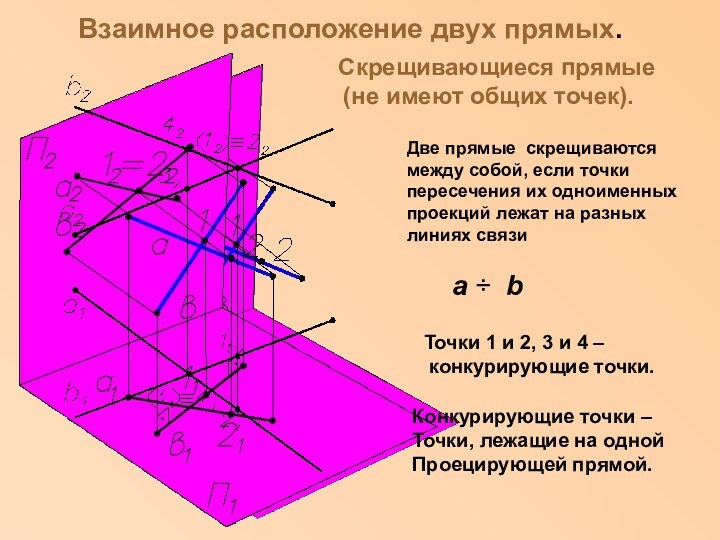
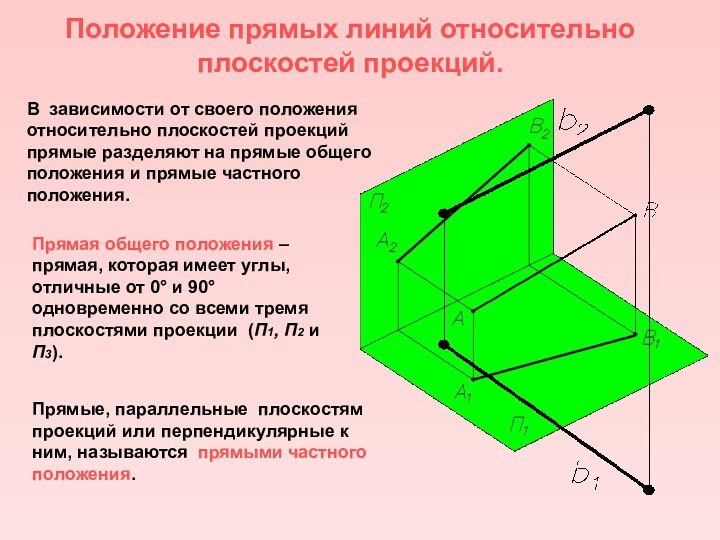
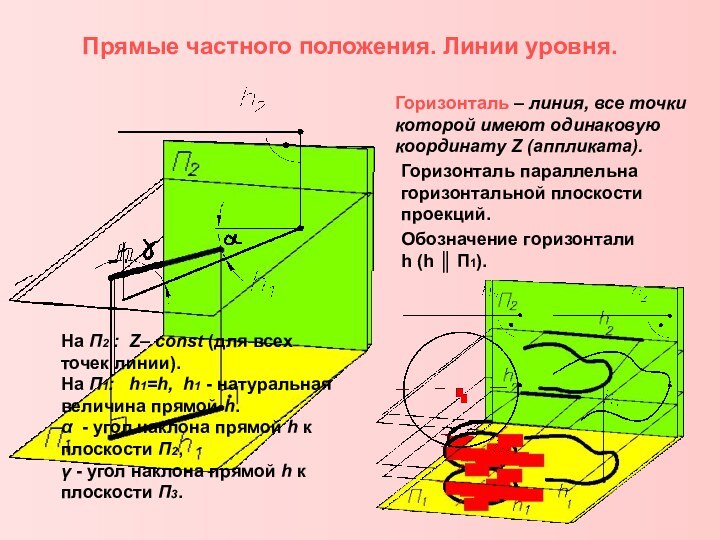
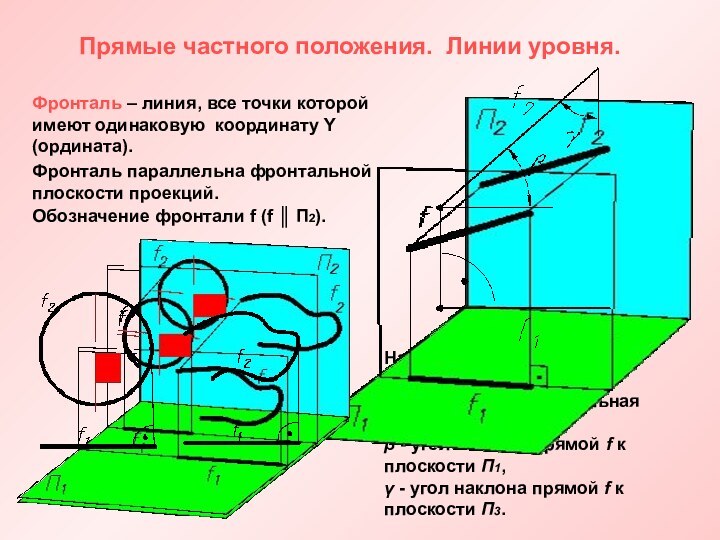
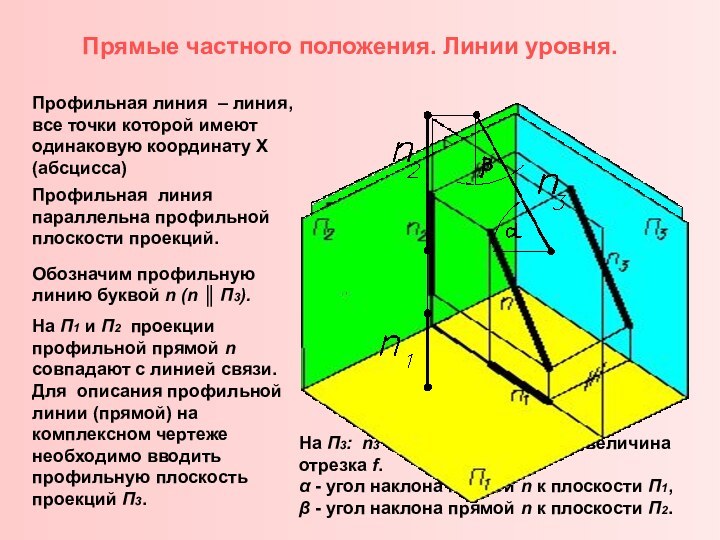
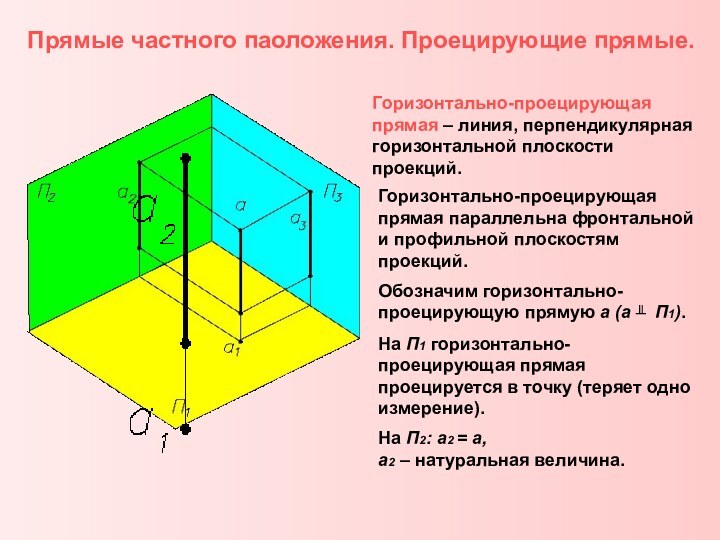
законы отображения трехмерного пространства на двумерную плоскость методами проекций

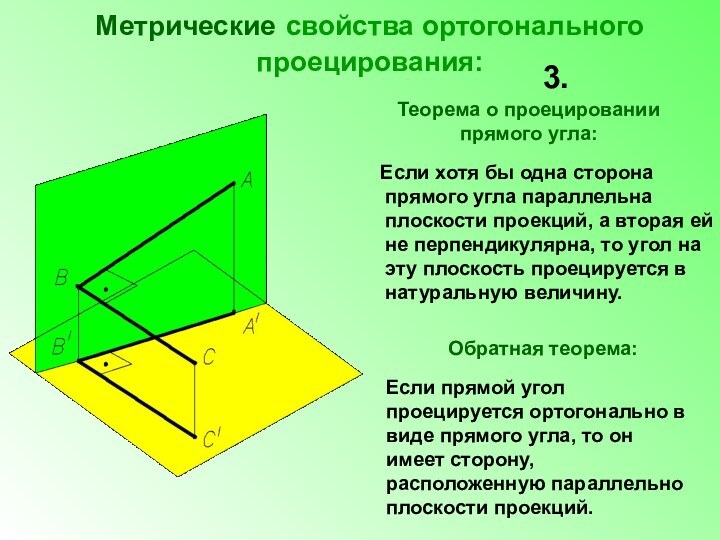
прямая -
построить изображение пространственного предмета на чертеже;

обратная –
реконструкция пространственного предмета по чертежу.

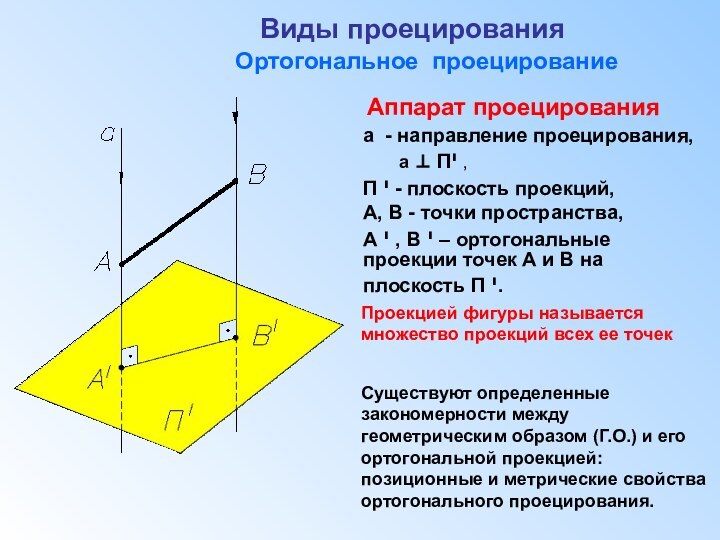
Построение любого изображения выполняется с помощью операции проецирования.

плоскость проекций или картинная плоскость,
А, В - точки

Аппарат проецирования

Проекцией фигуры называется множество проекций всех ее точек

Нет закономерных отношений между линейными размерами геометрического образа (Г.О.) и его проекциями.

проекций
А, В - точки пространства
Аי, Вי –

Аппарат проецирования

Проекцией фигуры называется множество проекций всех ее точек

Нет закономерных отношений между линейными размерами геометрического образа (Г.О.) и его проекциями.

,
П י - плоскость проекций,
А, В - точки

Проекцией фигуры называется множество проекций всех ее точек

Аппарат проецирования

Существуют определенные закономерности между геометрическим образом (Г.О.) и его ортогональной проекцией: позиционные и метрические свойства ортогонального проецирования.

соответствует одна точка на плоскости проекций,
А  Аי;

1.
(обратная

является прямая линия
Аי Вי,

АВ  Аי Вי;

АВАיВי– проецирующая

2.

то ее проекция принадлежит проекции данной линии,

С  АВ

3.

прямых является
точка пересечения проекций данных прямых;

D = АВ

4.

прямых являются
две параллельные прямые,

а II AB

5.

отрезками прямой равны соответствующим отношениям между их проекциями.

|АС| :

1.

проекции, делённой на косинус угла наклона отрезка к плоскости

2.

Примечания:
если α = 0о, то │АВ│=│АיВי│;
если α = 90о, то │АיВי│= 0.

Отрезок АВ (натуральная величина) является гипотенузой прямоугольного треугольника АВС, один катет которого является проекцией этого отрезка, а второй приращением координат точек А и В.

одна сторона прямого угла параллельна плоскости проекций, а вторая

3.

Если прямой угол проецируется ортогонально в виде прямого угла, то он имеет сторону, расположенную параллельно плоскости проекций.

Теорема о проецировании прямого угла:

Обратная теорема:

информации (введение второй плоскости проекции или числовой отметки, указывающей

Вышеприведенные чертежи называются однокартинными.

Рассмотренные методы проецирования позволяют однозначно решить прямую задачу – построить проекцию (чертеж) геометрического образа.

Обратная задача начертательной геометрии – по данному чертежу реконструировать геометрический образ – решается неоднозначно (может быть несколько или бесчисленное множество решений).

Из этого следует, что однокартинный чертеж не обладает свойством обратимости.

называется чертеж, составленный из двух или более связанных между

Принцип образования: геометрический образ ортогонально проецируется минимум на две взаимно перпендикулярные плоскости проекций, которые затем соответствующим образом совмещаются с одной плоскостью.

Данный чертеж называется комплексным чертежем (К.Ч.) точки А.

Если на К.Ч. заданы две проекции точки, можно утверждать, что точка однозначно задана на К.Ч.

осуществляется на три взаимно перпендикулярных плоскости проекций, и тогда

Условные обозначения:
A,В,С,D… 1,2,3… и т.д. – точки в пространстве;
П1 (XOY) – горизонтальная плоскость проекции;
П2 (XOZ) – вертикальная (фронтальная) плоскость проекции;
П3 (YOZ) – вертикальная (профильная) плоскость проекции;
А1 – горизонтальная проекция точки А на плоскость П1;
А2 – фронтальная проекция точки А на плоскость П2.
А3 – профильная проекция точки А на плоскость П3.
А1А2, А2А3 - линии связи.

сформированный последовательным перемещением точки.
Прямая однозначно задана на комплексном

Линия – одномерный геометрический образ.

Обозначение линий – a, b, c, d … и т.д.

параллельны между собой, то их одноименные проекции тоже параллельны.

Если

между собой, если точки пересечения одноименных проекций прямых лежат

Если a Х b = О,

то a1 Х b1 =О1
и a2 Х b2 = О2

точек).
Две прямые скрещиваются между собой, если точки пересечения их

а ÷ b

Точки 1 и 2, 3 и 4 –
конкурирующие точки.

Конкурирующие точки –
Точки, лежащие на одной
Проецирующей прямой.

положения относительно плоскостей проекций прямые разделяют на прямые общего

Прямая общего положения – прямая, которая имеет углы, отличные от 0° и 90° одновременно со всеми тремя плоскостями проекции (П1, П2 и П3).

Прямые, параллельные плоскостям проекций или перпендикулярные к ним, называются прямыми частного положения.

точки которой имеют одинаковую координату Z (аппликата).
Горизонталь параллельна горизонтальной

Обозначение горизонтали h (h ║ П1).

На П2 : Z– const (для всех точек линии).
На П1: h1=h, h1 - натуральная величина прямой h.
α - угол наклона прямой h к плоскости П2,
γ - угол наклона прямой h к плоскости П3.

точки которой имеют одинаковую координату Y (ордината).
Фронталь параллельна

Обозначение фронтали f (f ║ П2).

На П1 : Y – const (для всех точек прямой)
На П2: f2 = f, f2 - натуральная величина отрезка f.
β - угол наклона прямой f к плоскости П1,
γ - угол наклона прямой f к плоскости П3.

все точки которой имеют одинаковую координату X (абсцисса)
Профильная

Обозначим профильную линию буквой n (n ║ П3).

На П1 и П2 проекции профильной прямой n совпадают с линией связи. Для описания профильной линии (прямой) на комплексном чертеже необходимо вводить профильную плоскость проекций П3.

На П3: n3 = n, n3 - натуральная величина отрезка f.
α - угол наклона прямой n к плоскости П1,
β - угол наклона прямой n к плоскости П2.

перпендикулярная горизонтальной плоскости проекций.
Горизонтально-проецирующая
прямая параллельна фронтальной
и профильной плоскостям

Обозначим горизонтально-проецирующую прямую a (a ╨ П1).

На П1 горизонтально-проецирующая прямая проецируется в точку (теряет одно измерение).

На П2: а2 = а,
а2 – натуральная величина.