или состояния, определяющие ту или иную величину наблюдаемого признака
Результативные признаки – наблюдаемые признаки, которые испытывают влияние изучаемых факторовВарианты – отдельные значения результативного признака
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть




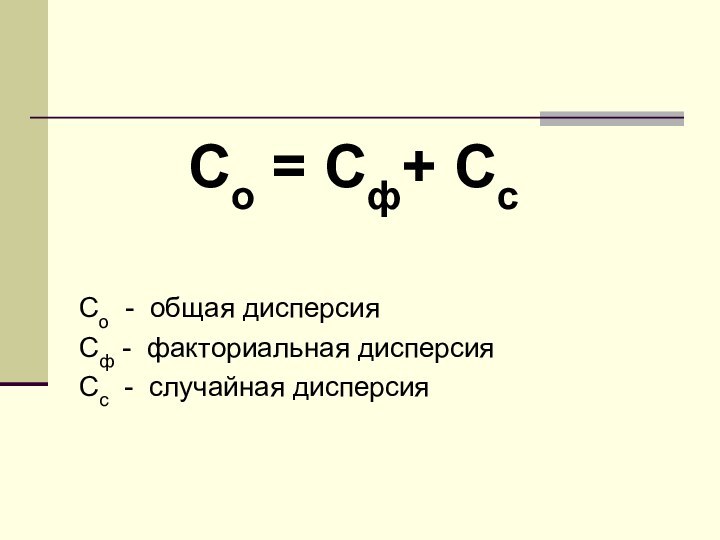












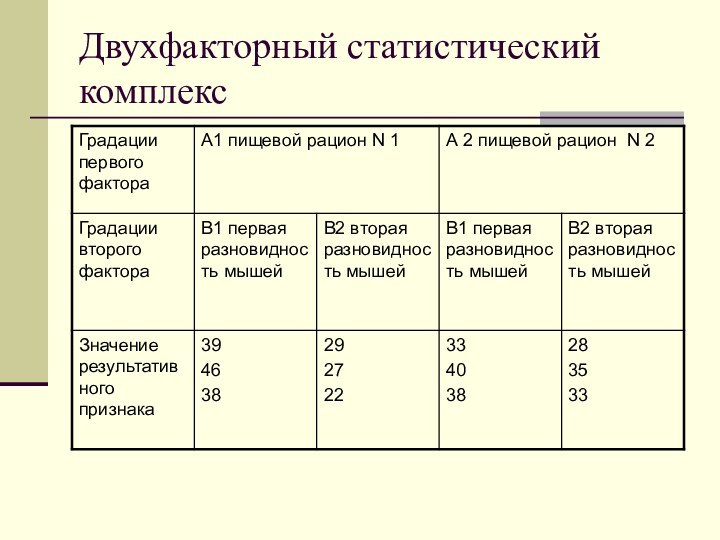
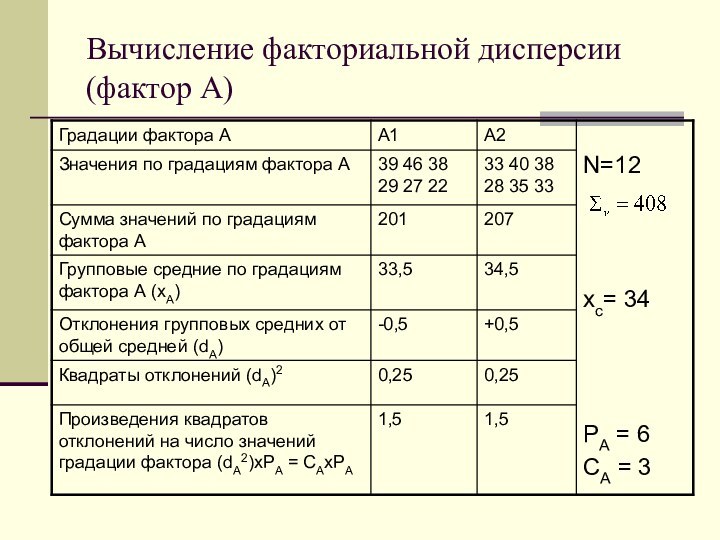
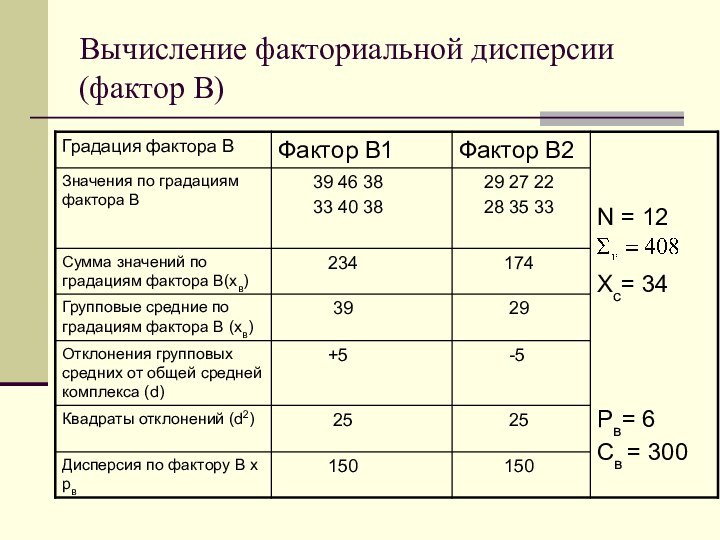

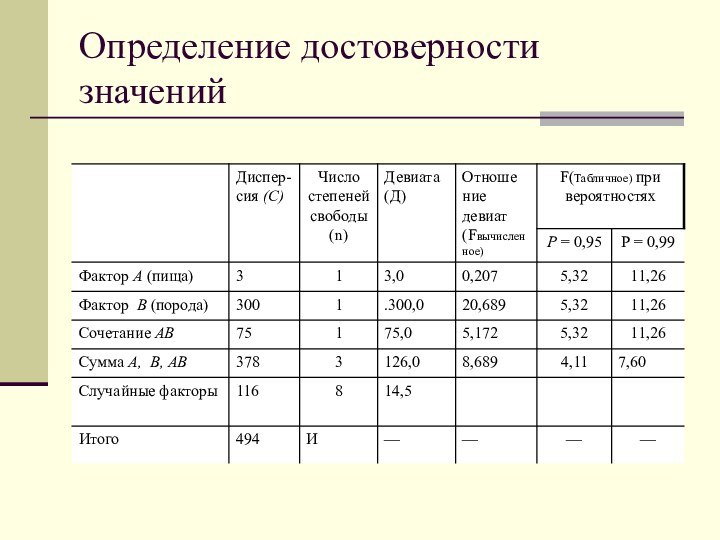

Вычисление общей дисперсии
3. Вычисление дисперсии суммарного действия
организованных факторов