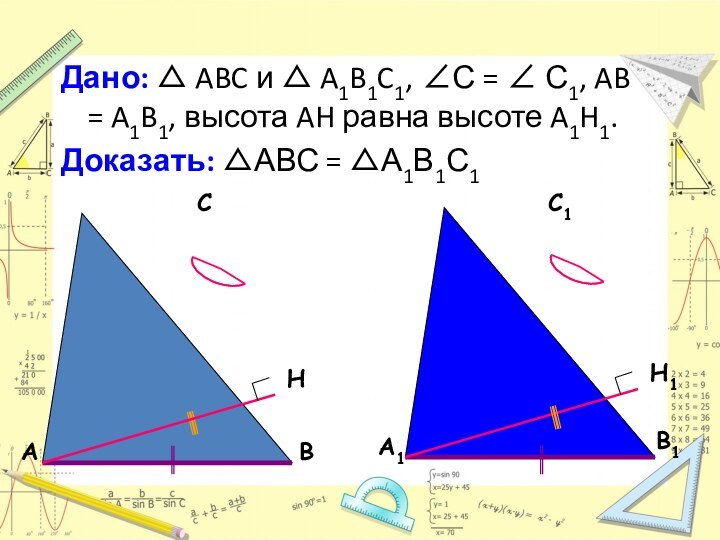
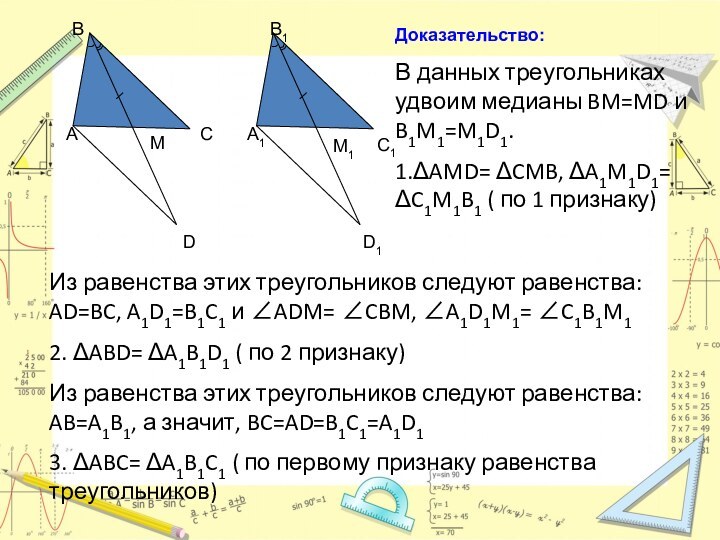
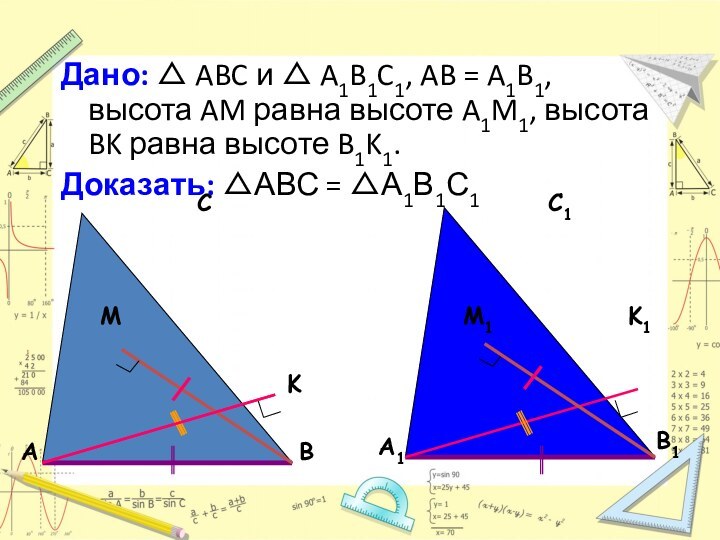
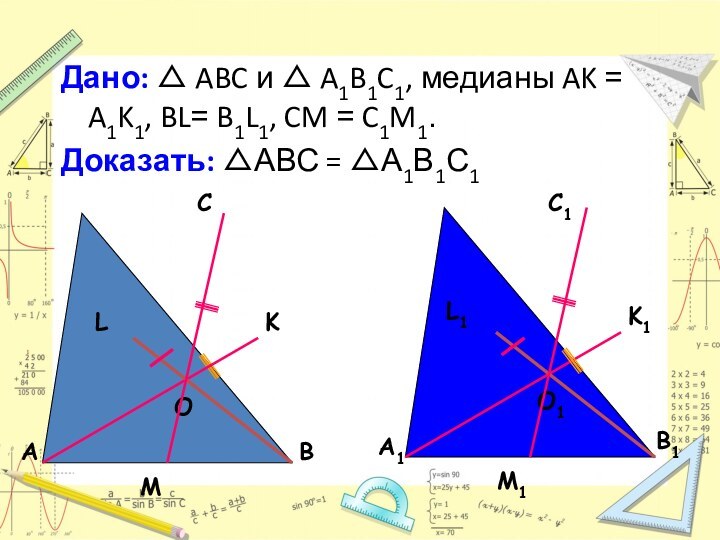
сторона, противолежащая этому углу, и высота, опущенная на другую
сторону, одного треугольника соответственно равны углу, стороне и высоте другого треугольника, то такие треугольники равны.Теорема 1
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть








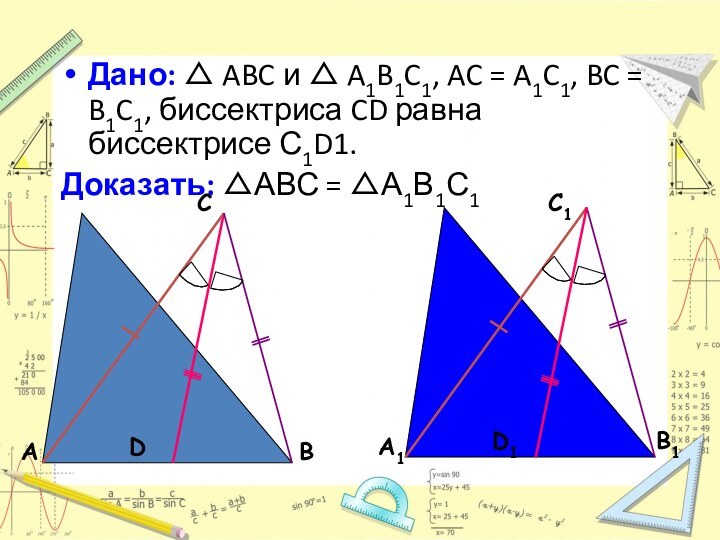

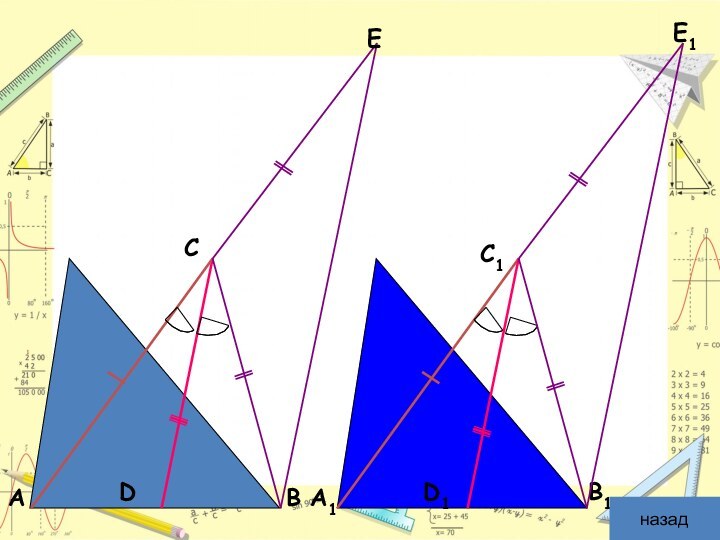

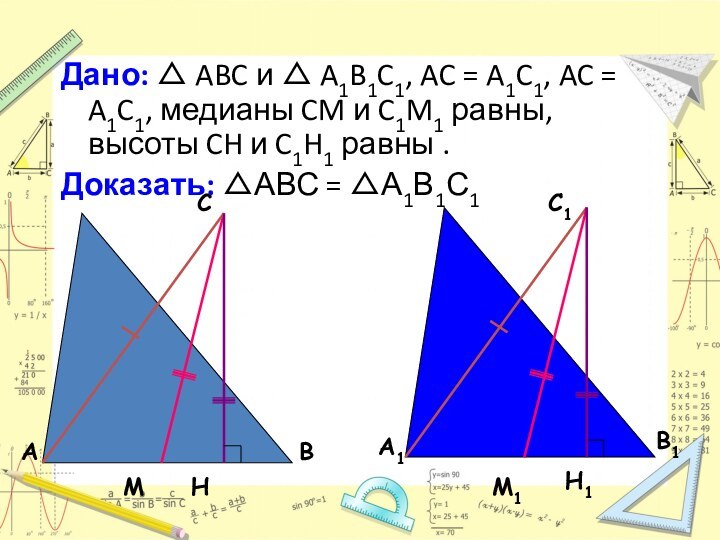


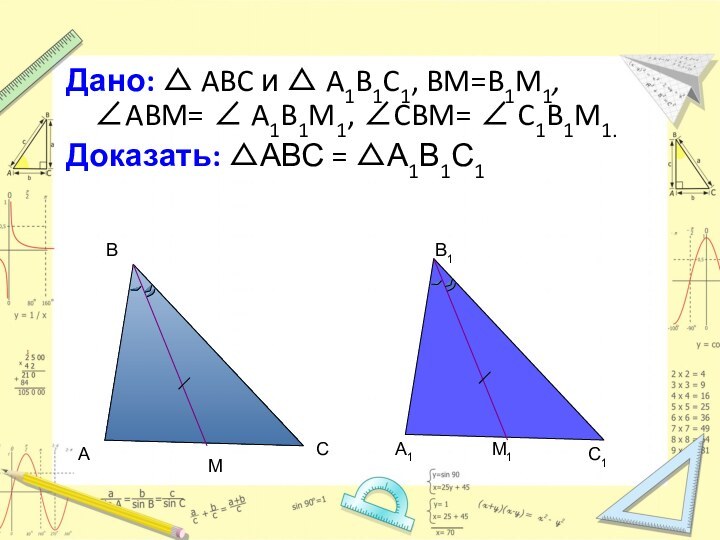







Теорема 1
H
H1
Теорема 2
Теорема 8
M
M1
чертеж
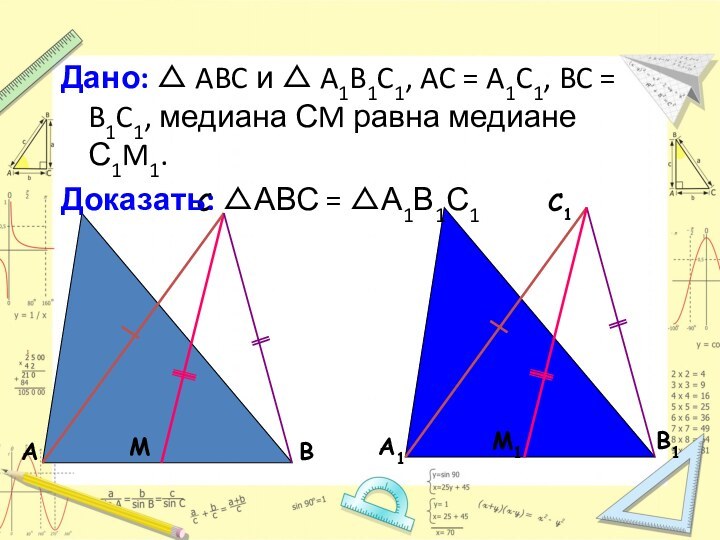
Теорема 3
M
M1
K
K1
O
O1
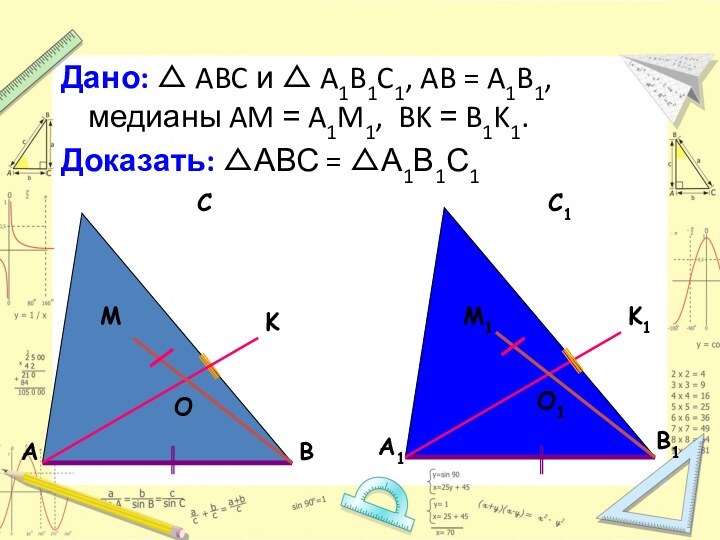
Теорема 4
D
D1
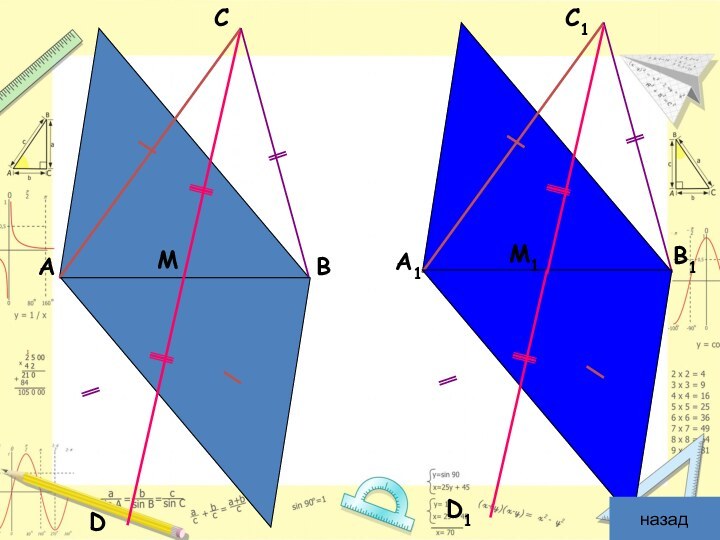
чертеж
Теорема 5
M
M1
H
H1
Теорема 6
Теорема 7
M
M1
K
K1
M
M1
K
K1
O
O1
L
L1
G
G1
H
H1
F
F1