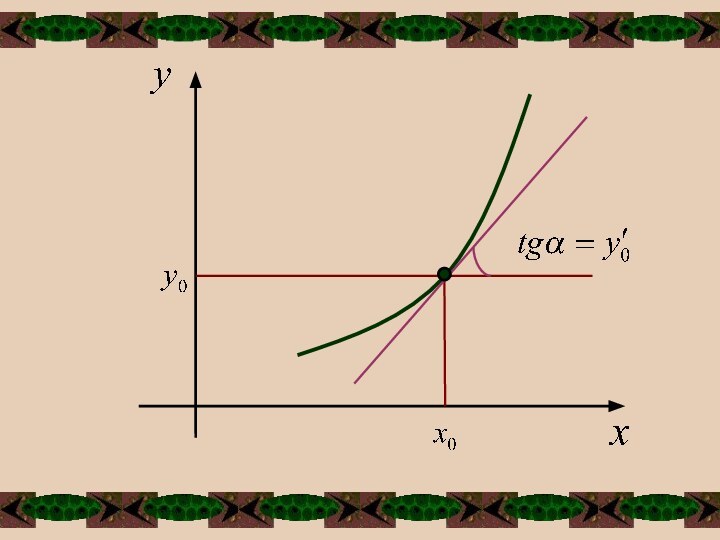
производной:
6
Решением ДУ второго порядка называется
функция у=φ(х), определенная на
некотором интервале
(a,b), котораяпри подстановке ее в уравнение
обращает его в тождество.