- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Две прямые, параллельные третьей прямой
Содержание
- 2. Теорема о параллельности трех прямых в пространствеЕсли две прямые параллельны третьей прямой, то они параллельныabсДано:Доказать:и
- 3. Теорема о параллельности трех прямых в пространствеЕсли
- 4. Теорема. Две прямые, параллельные третьей прямой, параллельны..Лемма.
- 5. Две прямые, лежащие в одной плоскости, и не имеющие общих точек, называются параллельнымиДоказательство от противного.
- 6. Дано: а || c; b || c.
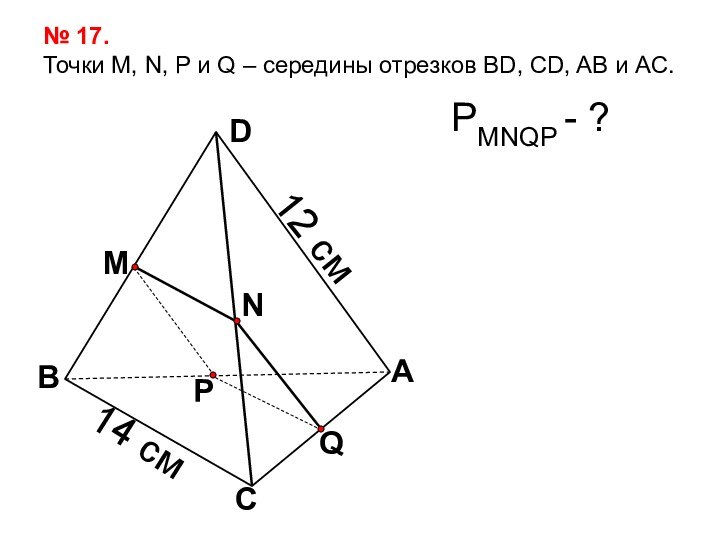
- 7. Задача №17.Дано: М – середина BD ABDCNMРQN
- 8. QАСВDNMP№ 17. Точки М, N, P и
- 9. Скачать презентацию
- 10. Похожие презентации
Теорема о параллельности трех прямых в пространствеЕсли две прямые параллельны третьей прямой, то они параллельныabсДано:Доказать:и



Слайд 2
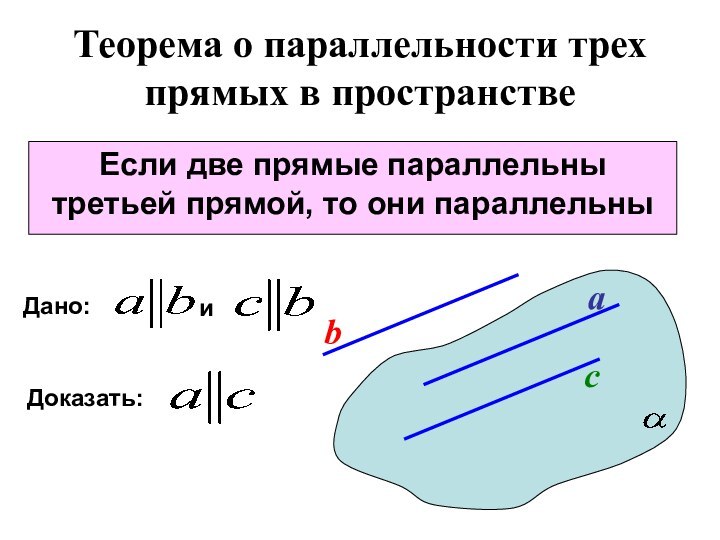
Теорема о параллельности трех прямых в пространстве
Если две
прямые параллельны третьей прямой, то они параллельны
Слайд 3
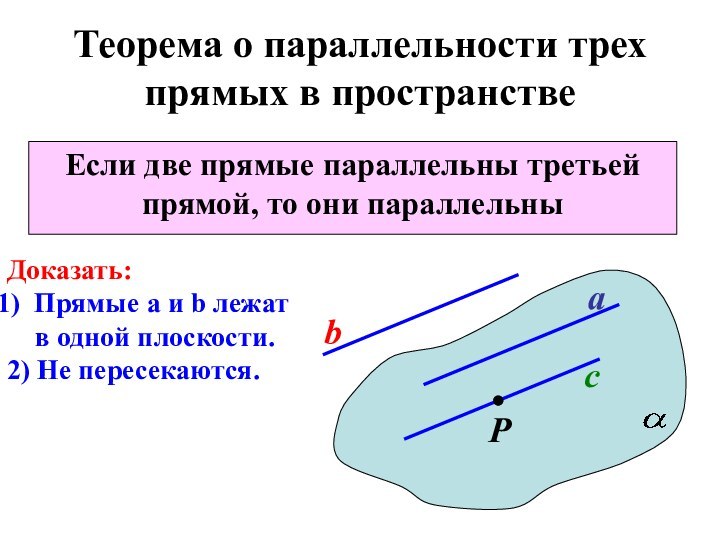
Теорема о параллельности трех прямых в пространстве
Если две
прямые параллельны третьей прямой, то они параллельны
a
b
с
Р
Доказать:
Прямые а и
b лежатв одной плоскости.
2) Не пересекаются.
Слайд 4
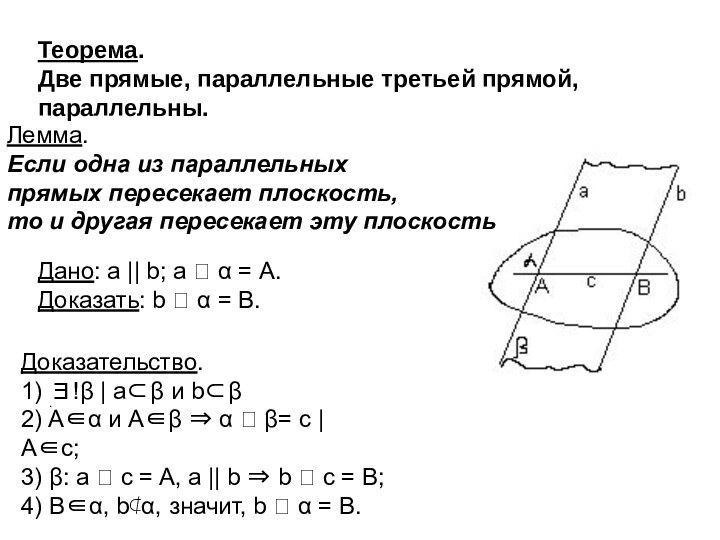
Теорема.
Две прямые, параллельные третьей прямой, параллельны.
.
Лемма.
Если
одна из параллельных
прямых пересекает плоскость,
то и другая
пересекает эту плоскостьДано: а || b; a = A.
Доказать: b = B.
Доказательство.
1) ! | а и b
2) A и A = c | Ac;
3) : a c = A, а || b b c = B;
4) B, b, значит, b = B.
Слайд 5
Две прямые, лежащие в одной плоскости,
и не
имеющие общих точек, называются параллельными
Доказательство от противного.
Слайд 6
Дано: а || c; b || c.
Доказать:
a || b.
Доказательство
Предположим, что а b = O,
тогда Оа, а || c и Оb, b || c –
противоречие с доказанной теоремой, то есть, а b = .
2) Предположим, что а и b не лежат в одной плоскости.
Рассмотрим Аа, тогда ! | А и b, причем, a = A.
По лемме, так как с || a, то c = C | Cb, поскольку с || b.
Следовательно, с b– противоречие.
Таким образом, a, b и а b = , то есть, а || b.
Слайд 7
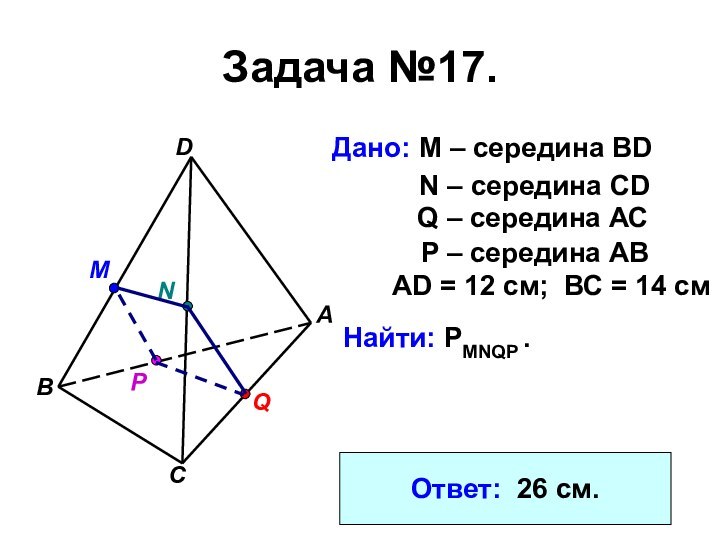
Задача №17.
Дано: М – середина BD
A
B
D
C
N
M
Р
Q
N –
середина CD
Q – середина АС
P – середина АВ
АD =
12 см; ВС = 14 смНайти: PMNQP .
Ответ: 26 см.