Презентация на тему Двусвязность. (Лекция 7)

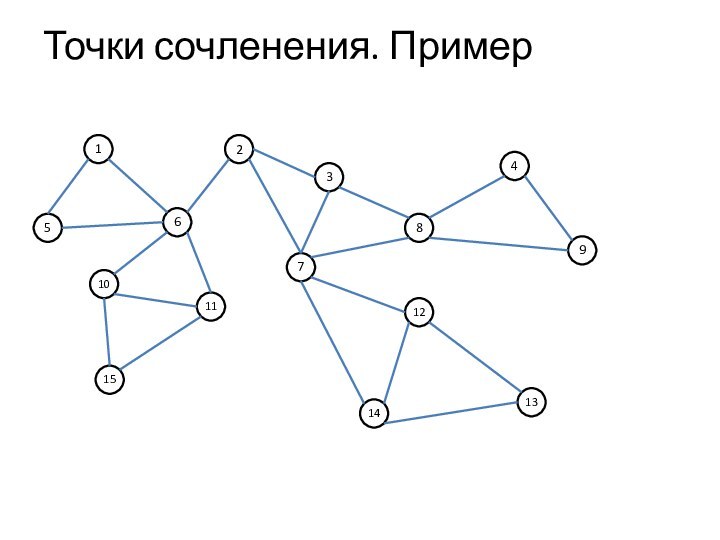
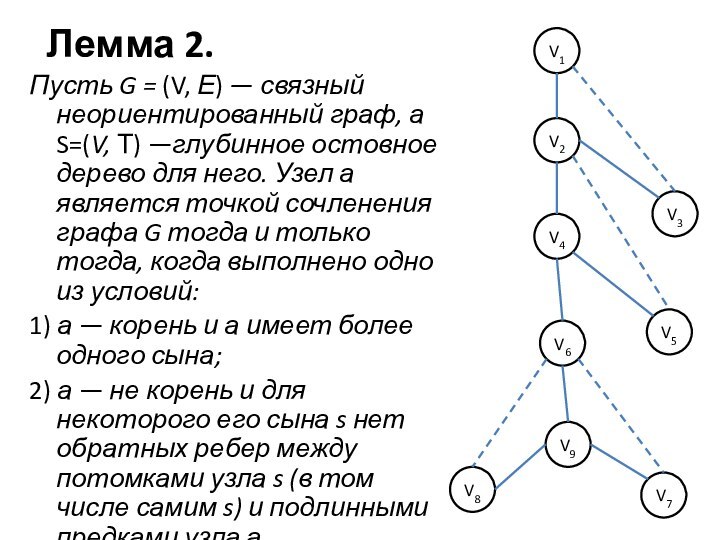
граф. Узел а называют точкой сочленения графа G, если

существуют такие узлы v и w, что v, w и а различны и всякий путь между v и w содержит узел а.
Иначе говоря, а — точка сочленения графа G, если удаление узла a расщепляет G не менее чем на две части.
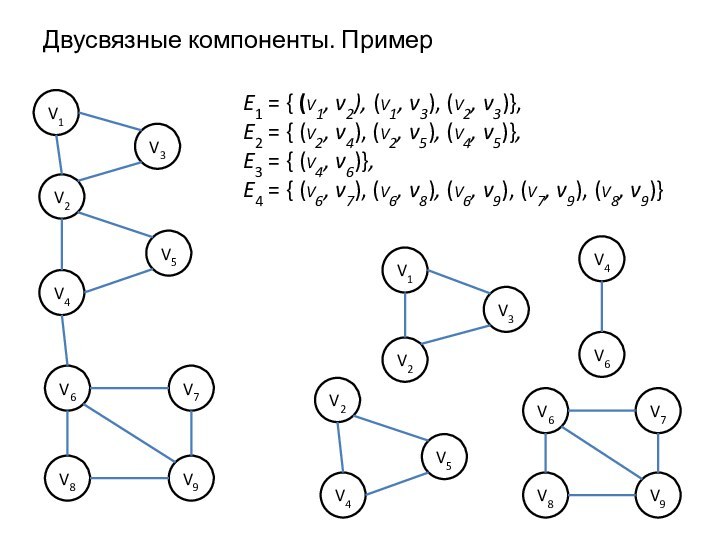
Граф G называется двусвязным, если для любой тройки различных узлов v, w, а существует путь между v и w, не содержащий а.
Таким образом, неориентированный связный граф двусвязен тогда и только тогда, когда в нем нет точек сочленения.

естественное отношение, полагая, что для ребер е1 и e2

выполняется это отношение, если e1= e2 или они лежат на некотором цикле.
Легко показать, что это отношение является отношением эквивалентности ( R называется отношением эквивалентности на множестве S, если R рефлексивно (aRa для всех а ∈ S), симметрично (из аRb следует bRа для всех а, b ∈ S) и транзитивно (из аRb и bRc следует аRc)), разбивающим множество ребер графа G на такие классы эквивалентности E1, Е2, . . ., Еk, что два различных ребра принадлежат одному и тому же классу тогда и только тогда, когда они лежат на общем цикле.
Для 1 ≤ i ≤ k обозначим через Vi множество узлов, лежащих на ребрах из Ei . Каждый граф Gi = (Vi, Ei) называется двусвязной компонентой графа G.

v3), (v2, v3)},
E2 = { (v2, v4), (v2, v5),

(v4, v5)},
E3 = { (v4, v6)},
E4 = { (v6, v7), (v6, v8), (v6, v9), (v7, v9), (v8, v9)}

i ≤ k — двусвязные компоненты связного неориентированного графа

G = (V, Е).

Тогда
1) граф Gi двусвязен для каждого i, 1 ≤ i ≤ k;
2) для всех i ≠ j пересечение Vi ∩Vj содержит не более одного узла;
3) а — точка сочленения графа G тогда и только тогда, когда а ∈ Vi ∩Vj для некоторых i ≠ j.

связный неориентированный граф, а S=(V, Т) —глубинное остовное дерево

для него. Узел а является точкой сочленения графа G тогда и только тогда, когда выполнено одно из условий:
1) а — корень и а имеет более одного сына;
2) а — не корень и для некоторого его сына s нет обратных ребер между потомками узла s (в том числе самим s) и подлинными предками узла а.

V1

V3

V2

V4

V5

V6

V7

V8

V9

в глубину
Для всех вершин v вычисляются числа dfnumber[v]. Они

фиксируют последовательность обхода вершин глубинного остовного дерева в прямом порядке.
Для каждой вершины v вычисляется число
dfnumber[v];
low[v] = min dfnumber[z], (v, z) – обратное ребро;
low[x], x – потомок v.
3. Точки сочленения определяются следующим образом:
корень остовного дерева будет точкой сочленения тогда и только тогда, когда он имеет двух и более сыновей;
вершина v, отличная от корня, будет точкой сочленения тогда и только тогда, когда имеет такого сына w, что
low[w] ≥ dfnumber [v].

неориентированный граф G= (V, Е).

Выход. Список ребер каждой

двусвязной компоненты графа G.

Метод.
Вначале полагаем Т=∅ и СЧЕТ=1. Помечаем каждый узел в V как "белый", выбираем произвольный узел v0 в V, отец[v0] = 0 и вызываем Поиск_дк(v0), чтобы построить глубинное остовное дерево S= (V,Т) и вычислить low[v] для каждого v из V.

← СЧЕТ; СЧЕТ ← СЧЕТ+1;
low[v] ← dfnumber[v] ;
для

∀ w ∈ смежные(v) выполнить
{    если (цвет[w] = белый) то
{ поместить (v, w) в СТЕК; добавить (v, w) к Т; отец [w] ← v;
Поиск_дк (w);
если low[w] ≥ dfnumber[v] то
{ обнаружена двусвязная компонента:
вытолкнуть из СТЕКа все ребра вплоть до ребра (v, w) ;
}
low[v] ← min ( low[v], low[w]);
}
иначе
если (w ≠ отец[v]) то
{ если (dfnumber[w] < dfnumber[v] ) то { поместить (v, w) в СТЕК;
low[v] ← min ( low[v], dfnumber[w] ) }
}
}
цвет[v] ← чёрный;
}

V6)
(V4, V5)
(V5, V2)
(V2, V3)
(V3, V1)
1
Стек