Презентация на тему ЕГЭ по математике 2013. Задачи С13

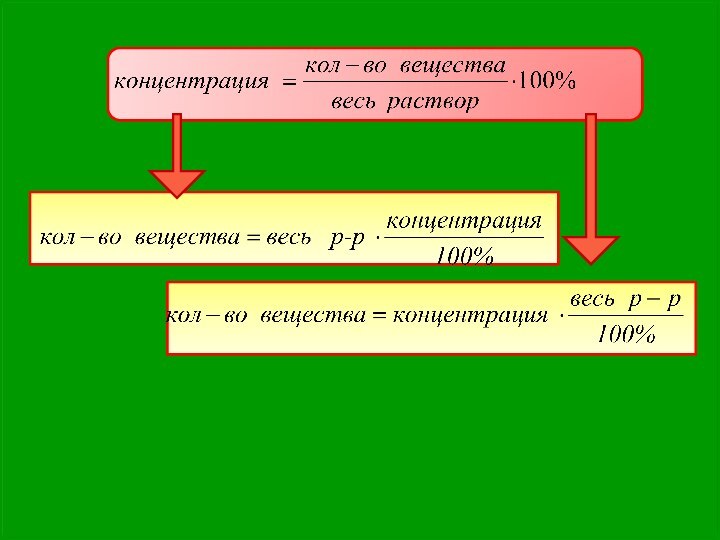
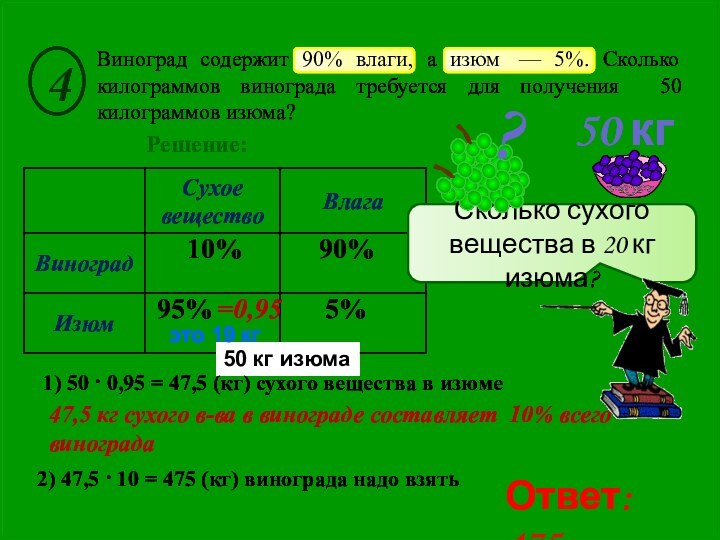
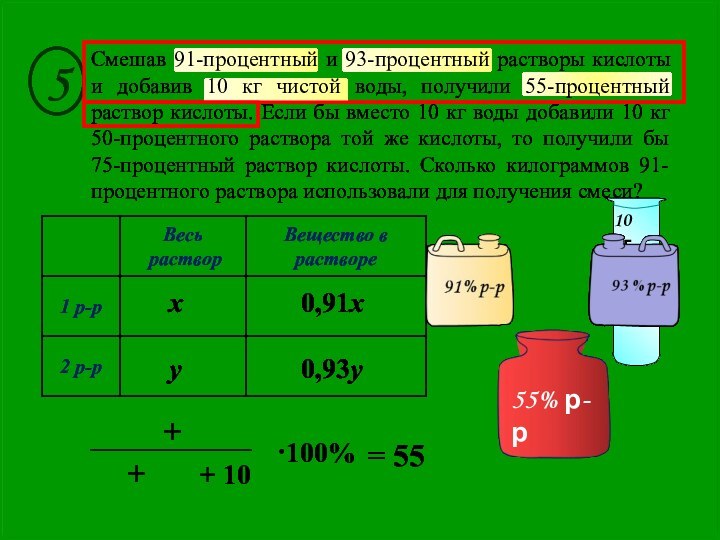
условия задачи. Выбрать неизвестные величины (их обозначают буквами х, у и

т.д.), относительно которых составить пропорции, этим, мы создаем математическую модель ситуации, описанной в условии задачи.
Используя условия задачи, определить все взаимосвязи между данными величинами.
Составить математическую модель задачи и решить ее.
Изучить полученное решение, провести критический анализ результата.

в растворе
12% = 0,12


Ответ: 4
Решение:
Сколько вещества было в растворе?
5

л
12% р-р

7 л

Задачи 17-18

таким же количеством 21-процентного раствора этого вещества. Сколько процентов

составляет концентрация получившегося раствора?

x

0,15x

0,21x

+

2

Ответ: 18

15% = 0,15

21% = 0,21

Решение:

x

x

x

0,15x

0,21x

Задачи 19-20

с 6 литрами 25-процентного водного раствора этого же вещества.

Сколько процентов составляет концентрация получившегося раствора?

6

4

0,6

1,5

+

1) 4 · 0,15 = 0,6 (л) вещества в 1 растворе

2) 6 · 0,25 = 1,5 (л) вещества во 2 растворе

3

15% = 0,15

25% = 0,25

Решение:

Сколько вещества было в растворе?

4

6

0,6

1,5

Ответ: 21

Задачи 21-22

 — 5%. Сколько килограммов винограда требуется для получения 50

килограммов изюма?

5%

50 кг изюма

1) 50 · 0,95 = 47,5 (кг) сухого вещества в изюме

это 19 кг

47,5 кг сухого в-ва в винограде составляет 10% всего винограда

2) 47,5 · 10 = 475 (кг) винограда надо взять

4

Решение:

Сколько сухого вещества в 20 кг изюма?

?

50 кг

Ответ: 475

=0,95

10 кг чистой воды, получили 55-процентный раствор кислоты. Если

бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 75-процентный раствор кислоты. Сколько килограммов 91-процентного раствора использовали для получения смеси?

y

0,91x

x

+

+ 10

= 55

5

55% р-р

x

y

0,91x

0,93y

·100%

10 кг чистой воды, получили 55-процентный раствор кислоты. Если

бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 75-процентный раствор кислоты. Сколько килограммов 91-процентного раствора использовали для получения смеси?

x

y

0,91x

x

+

+ 10

= 75

10 · 0,5 = 5 (кг) кислоты в р-ре

+ 5

?

Искомая величина

50% = 0,5

· 100

второй  — 20 кг раствора кислоты различной концентрации. Если

эти растворы смешать, то получится раствор, содержащий 68% кислоты. Если же смешать равные массы этих растворов, то получится раствор, содержащий 70% кислоты. Сколько килограммов кислоты содержится в первом сосуде?

= 68

30

20

0,3x

0,2y

6

30

20

1 уравнение

?

0,3x

0,2y

второй  — 20 кг раствора кислоты различной концентрации. Если

эти растворы смешать, то получится раствор, содержащий 68% кислоты. Если же смешать равные массы этих растворов, то получится раствор, содержащий 70% кислоты. Сколько килограммов кислоты содержится в первом сосуде?

0,01y

1

1

0,01x

= 70

Возьмем по 1 кг

1

1

2 уравнение

0,01x

0,01y

второй  — 10% никеля. Из этих двух сплавов получили

третий сплав массой 100 кг, содержащий 12% никеля. На сколько килограммов масса первого сплава меньше массы второго?

= 12

7

30%=0,3

x

y

10%=0,1

30

10

0,3x

0,1y

Ответ: 80

меди. Масса второго сплава больше массы первого на 3

кг. Из этих двух сплавов получили третий сплав, содержащий 30% меди. Найдите массу третьего сплава. Ответ дайте в килограммах.

0,1x

= 30

8

x

x+3

0,1x

0,4(x+3)

Ответ: 9

10%=0,1

40%=0,4