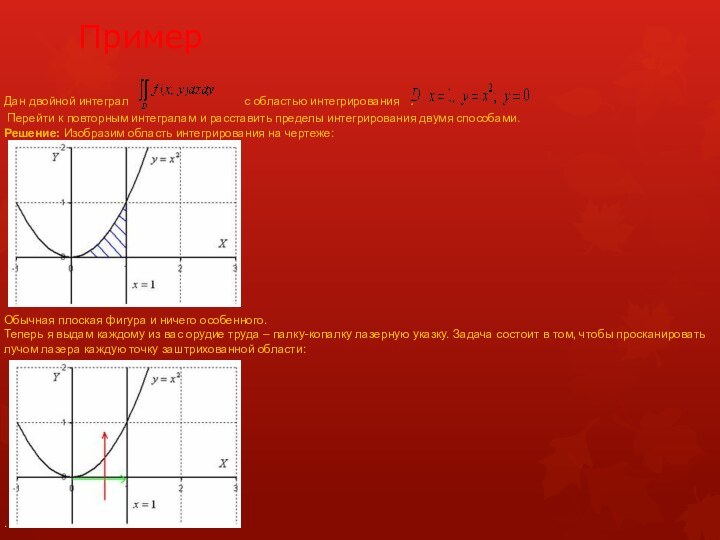
есть указку вы ВСЕГДА держите ниже плоской фигуры. Луч входит в
область через ось абсцисс, которая задаётся уравнением и выходит из области через параболу (красная стрелка). Чтобы просветить всю область, вам нужно строго слева направо провести указкой вдоль оси ОХ от 0 до 1 (зелёная стрелка).
Итак, что получилось:
«игрек» изменяется от 0 до ;
«икс» изменяется от 0 до 1.
В задачах вышесказанное записывают в виде неравенств:
Данные неравенства называют порядком обхода области интегрирования или простопорядком интегрирования
После того, как мы разобрались с порядком обхода, можно перейти от двойного интеграла к повторным интегралам:
Половина задачи решена. Теперь необходимо перейти к повторным интегралам вторым способом. Для этого следует найти обратные функции. Кто ознакомился со вторым параграфом урока Объем тела вращения, тому будет легче. Смотрим на функции, которыми задается область . Если совсем просто, то перейти к обратным функциям, это значит – выразить «иксы» через «игреки». Единственной функцией, где есть и «икс» и «игрек», является .
Если , то , причём:
обратная функция задает правую ветку параболы;
обратная функция задает левую ветку параболы.
Нередко возникают сомнения, вот, к примеру, функция определяет левую или правую ветвь параболы? Сомнения развеять очень просто: возьмите какую-нибудь точку параболы, например, (1,1) (с правой ветви) и подставьте её координаты в любое уравнение, например, в то же уравнение :
Получено верное равенство, значит, функция определяет именно правую ветвь параболы, а не левую.
.