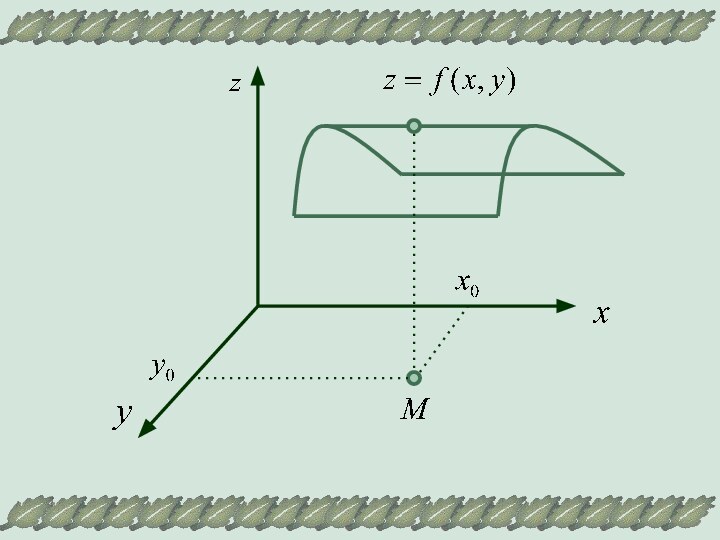
существует окрестность точки М,
такая что для всех точек
(х,у) из этойокрестности выполняется неравенство:
max
min
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть






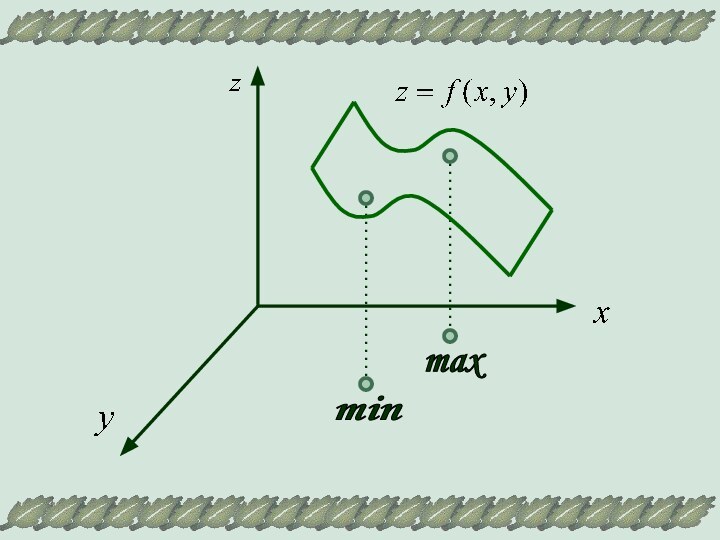











max
min
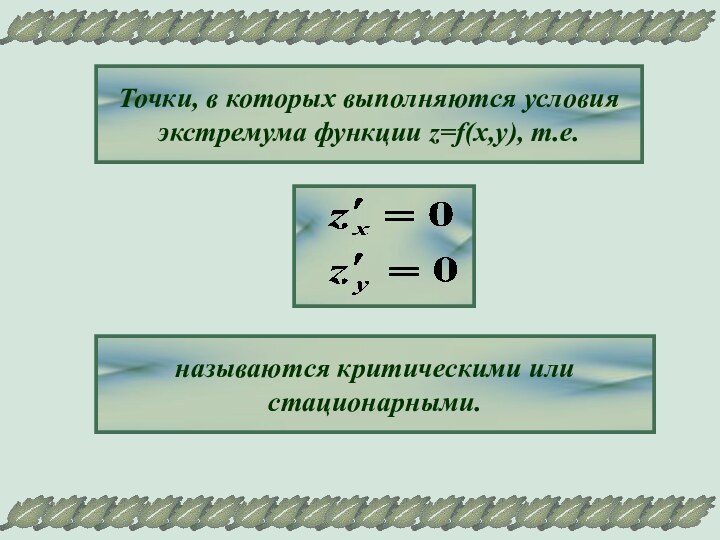
необходимое условие
экстремума
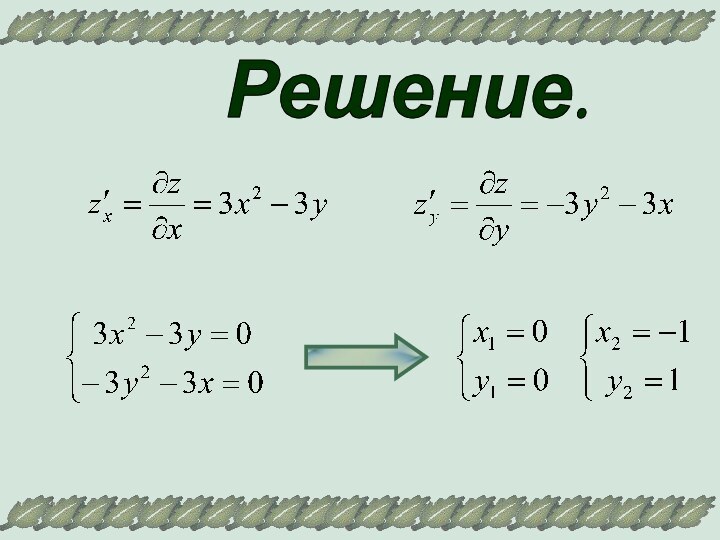
Аналогично можно доказать, что
то вопрос остается открытым.