- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Элементы комбинаторики
Содержание
- 2. Принцип произведения комбинацийN = n1 ∙ n2 ∙ … ∙ nk
- 3. Принцип произведения комбинацийПусть имеется k групп элементов,
- 4. Виды комбинацийПерестановкиРазмещенияСочетания
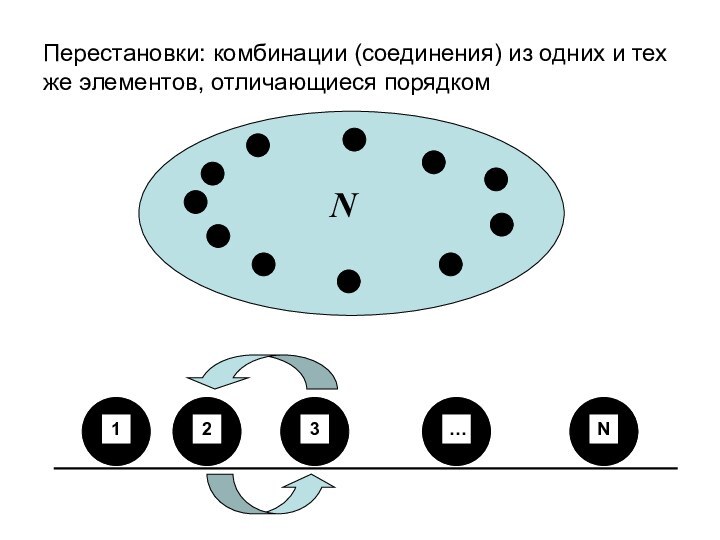
- 5. Перестановки: комбинации (соединения) из одних и тех же элементов, отличающиеся порядком
- 6. Подсчитаем число перестановок. Используем принцип произведения комбинаций:
- 7. Размещения из N элементов по m элементов–
- 8. Сочетания из N элементов по m элементов–
- 9. Основное свойство сочетанийОбразование сочетаний связано с задачей
- 10. «Урновые» схемы проведения случайных экспериментовУрна (ящик), содержит
- 11. Выбор без возвращения с учетом порядкаВыбор без возвращения без учета порядка
- 12. Выбор с возвращением с учетом порядкаОбщее количество выборок :Выбор с возвращением без учета порядкаДва из двух
- 13. Скачать презентацию
- 14. Похожие презентации
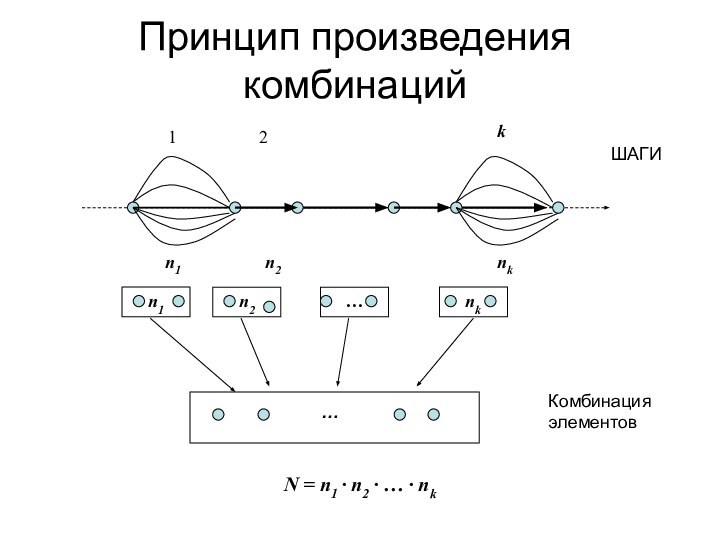
Принцип произведения комбинацийN = n1 ∙ n2 ∙ … ∙ nk








Слайд 3
Принцип произведения комбинаций
Пусть имеется k групп элементов, причем
i-я группа содержит ni элементов, 1 ≤ i ≤
k.Выберем из каждой группы по одному элементу.Тогда общее число N способов, которыми можно произвести такой выбор, равняется
N = n1 ∙ n2 ∙ … ∙ nk
Слайд 7
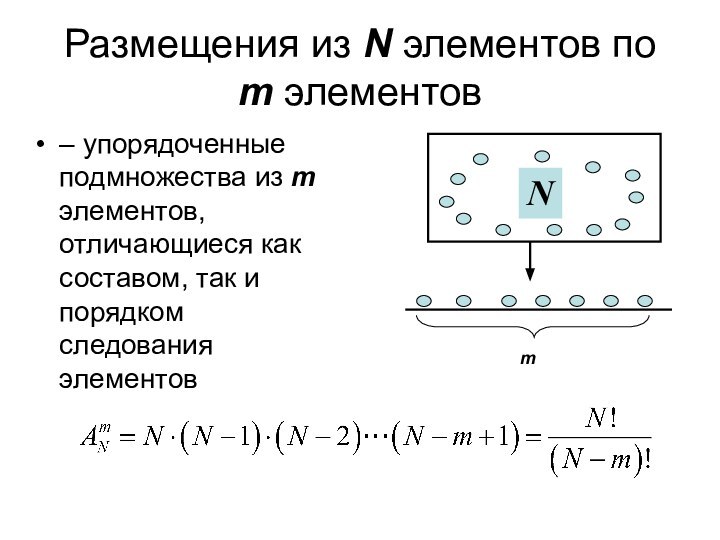
Размещения из N элементов по m элементов
– упорядоченные
подмножества из m элементов, отличающиеся как составом, так и
порядком следования элементов
Слайд 8
Сочетания из N элементов по m элементов
– неупорядоченные
подмножества из m элементов, отличающиеся только составом элементов.
Если в
каждом сочетании произвести все возможные m! перестановок, то мы получим все размещения.Число размещений и число сочетаний
Связаны соотношением:
Отсюда имеем:
Слайд 9
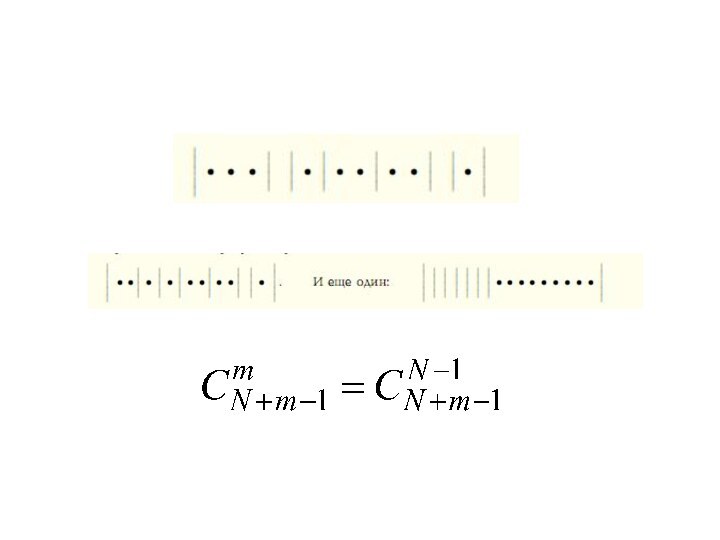
Основное свойство сочетаний
Образование сочетаний связано с задачей разбиения
множества N элементов на два подмножества так, что одно
из них содержит m элементов, а другое – оставшиеся (N-m) элементов и является простейшим случаем более общей задачи о разбиении множества на k неупорядоченных подмножеств, содержащих n1, n2, … , nk элементов, причем n1 + n2 + … + nk = N.Число таких комбинаций равно
Слайд 10
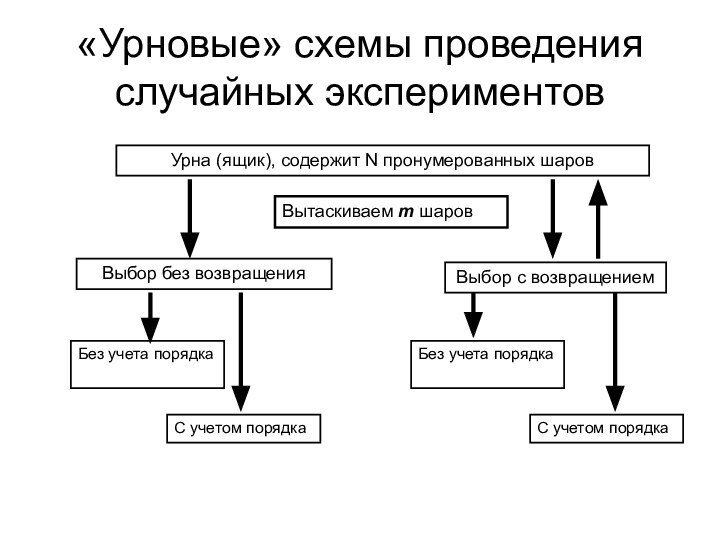
«Урновые» схемы проведения случайных экспериментов
Урна (ящик), содержит N
пронумерованных шаров
Выбор с возвращением
Выбор без возвращения
Без учета порядка
Без учета
порядкаС учетом порядка
С учетом порядка
Вытаскиваем m шаров





























