- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Элементы комбинаторики
Содержание
- 2. Комбинаторика – это раздел математики, посвящённый задачам
- 3. Вспомним несколько примеров таких задач1.Несколько стран в
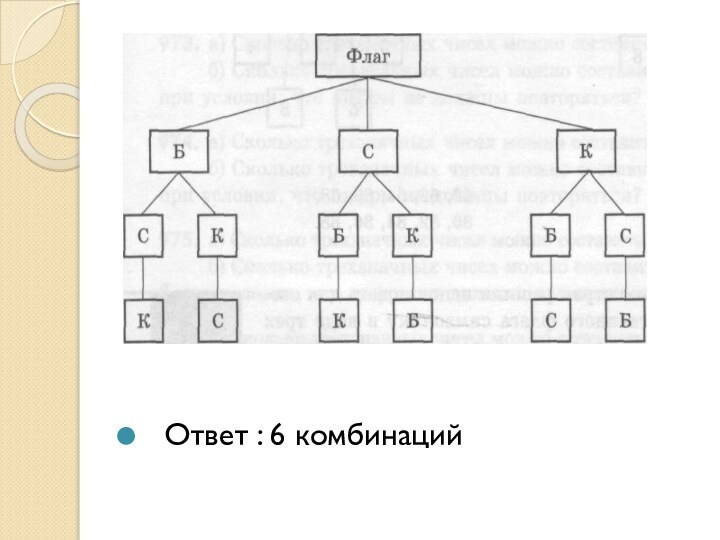
- 4. Ответ : 6 комбинаций
- 5. 2.Сколько чётных двузначных чисел можно составить из
- 6. Так в столбце перечислены все возможные варианты,
- 7. 3.На завтрак Вова может выбрать плюшку, бутерброд,
- 8. Во всех задачах был осуществлён перебор всех
- 9. Мы рассмотрели примеры 3-х разных задач, но
- 10. Решение задач в классе :
- 11. Решение. Что бы указать все обеды
- 12. № 716 Стадион
- 13. Решение. Из условия ясно, что
- 14. №718. Составьте все возможные двузначные числа
- 15. Решение. а) Выбираем поочерёдно:16, 18, 61, 68, 81, 86. Всего 6 различных чисел
- 16. №721. В шахматном турнире
- 17. Решение. Поскольку
- 18. Скачать презентацию
- 19. Похожие презентации
Комбинаторика – это раздел математики, посвящённый задачам выбора и расположения предметов из раздела множеств. Типичной задачей комбинаторики является задача перечисления комбинаций, составленных из нескольких предметов.

















Слайд 3
Вспомним несколько примеров таких задач
1.Несколько стран в качестве
символа своего государства решили использовать флаг в виде 3-х
горизонтальных полос одинаковых по ширине и цвету: синий, красный и белый. Сколько стран могут испытать такую символику при условии, что у каждой страны свой отличный от других флаг? Будем искать решение с помощью дерева возможных вариантов.
Слайд 5 2.Сколько чётных двузначных чисел можно составить из цифр
0,1,2,4,5,9.
Составим таблицу: слева от 1 – го столбца
поместим первые цифры искомых чисел, сверху – вторые цифры этих чисел (чётные цифры, тогда столбцов будет три).Слайд 6 Так в столбце перечислены все возможные варианты, следовательно,
их столько же, сколько клеток в столбце, т.е. 15.
Ответ:
15 чиселСлайд 7 3.На завтрак Вова может выбрать плюшку, бутерброд, пряник
или кекс, а запить их может кофеем, соком или
кефиром. Из скольких вариантов завтрака Вова может выбирать?Решим задачу, перебирая всевозможные варианты, путем кодирования вариантов завтрака
Решение: КП КБ КПр КК
СП СБ СПр СК
К-рП К-рБ К-рПр К-рК
Ответ: 12 вариантов.
Слайд 8 Во всех задачах был осуществлён перебор всех возможных
вариантов или комбинаций. Поэтому эти задачи называют комбинаторными. Слово
комбинация происходит от латинского combino – соединяю.Действительно при получении любой комбинации мы составляем её из отдельных элементов последовательно соединяя их друг с другом. С этой точки зрения: число – это комбинация цифр, слово – это комбинация букв, меню – это комбинация блюд.
Во всех предложенных задачах для подсчёта числа комбинаций мы использовали простой способ подсчёта – прямое перечисление (опираясь на «дерево возможных вариантов», таблицу, кодирование). Но способ перебора возможных вариантов далеко не всегда применим, ведь количество комбинаций может исчисляться миллионами.
Здесь на помощь приходят несколько замечательных комбинаторных правил, которые позволяют подсчитать количество комбинаций без их прямого перечисления.
Слайд 9 Мы рассмотрели примеры 3-х разных задач, но получили
совершенно одинаковые решения, которые основаны на общем правиле умножения:
Пусть
имеется n элементов и требуется выбрать из них один за другим к элементов. Если первый элемент m1выбрать n1 способами, после чего второй элемент m2 выбрать n2 способами из оставшихся, затем третий элемент m3 выбрать n3 способами из оставшихся и т.д., то число способов могут быть выбраны все к элементов, равно произведению Примени это правило к каждой из решённых задач.
1-я задача: выбор верхней полосы - из 3-х цветов, т.е. n1=3; средняя полоса – из 2-х цветов, т.е.n2=2; нижняя полоса – из 1-го цвета, т.е. n3=1.
n1 n2 n3 = 3 * 2 * 1 = 6
2-я задача: заметим, что в этой задаче задействованы два независимых исхода, поэтому m n = 5 *3 = 15
Слайд 10 Решение задач в классе : №
714, 716,718(а),721
№714.
В кафе предлагают два первых блюда:
борщ, рассольник — и четыре вторых блюда: гуляш, котлеты, сосиски, пельмени. Укажите все обеды из первого и второго блюд, которые может заказать посетитель. Проиллюстрируйте ответ, построив дерево возможных вариантов.
Слайд 11
Решение.
Что бы указать все обеды из
двух блюд, будем рассуждать так.
Выберем одно блюдо
(борщ) и будем добавлять к нему поочерёдно разные вторые блюда, получая пары:Б г; б к; б с; б п (4 пары).
Теперь в качестве первого блюда выберем рассольник и будем добавлять к нему поочерёдно разные вторые блюда:
Рг; р к; р с; р п (4 пары).
Согласно правилу комбинаторного умножения всего обедов: 2*4=8.
Построив дерево возможностей, получим 8 вариантов.
Ответ: б г; б к; б с; б п; р г; р к; р с; р п.; получим восемь разных обедов из двух блюд.
Слайд 12
№ 716
Стадион имеет
четыре входа: А, В, С и D. Укажите все
возможные способы, какими посетитель может войти через один вход, а выйти через другой. Сколько таких способов?
Слайд 13
Решение.
Из условия ясно, что порядок
выбора имеет значение: АВ означает, что посетитель вошёл через
А и вышел через В, а ВА означает, что вошёл через В, а вышел через А.Чтобы перечислить все варианты выбора двух входов, будем придерживаться следующего правила.
Выпишем обозначения всех входов в ряд: А, В, С, Д. Берём первый вход и дописываем к нему поочерёдно каждый из остальных входов, получаем 3 пары: А В, А С, А Д.
Берём второй вход и дописываем к нему поочерёдно каждый из остальных входов, кроме него самого начиная с начала ряда, т. е. с первого входа: ВА, ВС, ВД.
Выбирая третий, а затем четвёртый вход, получаем СА, СВ, СД; ДА, ДВ, ДС.
Общее количество способов выбора: 4*3=12 (к каждому из 4 входов мы дописывали 3 других).
Замечание. Подсчитать количество способов выбора, не составляя пары, можно по правилу произведения: первый выбор (через какой вход войти) можно сделать 4 способами (А, или В, или С, или Д); после этого второй выбор (через какой вход войти) можно сделать 3 способами ( любой вход, кроме того, через который вошли). Общее количество выбора равно 4*3=12.
Ответ: 12 способов.
Слайд 14
№718.
Составьте все возможные двузначные числа
из указанных цифр, используя в записи числа каждую из
них не более одного раза:а) 1, 6, 8;
Слайд 16
№721.
В шахматном турнире участвуют
9 человек. Каждый из них сыграл с
каждым по
одной партии. Сколько всего партий было сыграно?
Слайд 17
Решение.
Поскольку
каждая пара участников играла между собой только один раз,
порядок выбора не имеет значения (когда Иванов играл с Петровым, это то же самое, что Петров играл с Ивановым).Выбрать первого участника партии можно 9 способами, а второго- 8 оставшимися способами; по правилу произведения всего можно образовать 9*8=72 пары,
но в это число каждая пара входит дважды: сначала Иванов-Петров, затем Петров- Иванов.
Поскольку порядок выбора не имеет значения, то общее количество партий равно .
Ответ: 36 партий.





























