Слайд 2
Литература и интернет - ресурсы
Гмурман В.Е. Теория вероятностей
и математическая статистика: Учеб. пособие. – М.: Высшее образование,
2006. – 479 с.
Гмурман В.Е. Руководство к решению задач по теории вероятностей и математическая статистика: Учеб. пособие. – М.: Высшее образование, 2006. – 404 с.
http://e-lib.uspu.ru
www.exponenta.ru
Слайд 3
Введение. Основные понятия
математической статистики
Определение: Основной задачей математической
статистики (МС) считают создание методов сбора и обработки экспериментальных
данных с целью получения достоверной информации о случайной величине, интересующей экспериментатора.
Более подробно: Первая задача МС – указать способы сбора и группировки статистических сведений, полученных в результате наблюдений или специально поставленных экспериментов.
Вторая задача МС – разработать методы анализа статистических данных в зависимости от целей исследования.
Сюда относятся: (а) Оценка неизвестной вероятности события; оценка неизвестной функции распределения, оценка параметров распределения вид которого известен; оценка зависимости с.в. от одной или нескольких случайных величин и др.;
(б) Проверка статистических гипотез о виде неизвестного распределения или о величине параметров распределения, вид которого известен.
Слайд 4
Генеральная и выборочная совокупности. Дискретный вариационный ряд. Полигон
частот. Гистограмма.
Определение: Множество всех объектов, подлежащих изучению, называется генеральной
совокупностью. На языке теории множеств аналогом генеральной совокупности является универсальное множество.
З а м е ч а н и е: Часто сплошное изучение (по качественному или количественному признаку) всех элементов генеральной совокупности сопряжено со значительными трудностями: большое число объектов в совокупности, необходимость уничтожения объектов при проведении некоторых видов испытаний и др. В этом случае приходится ограничиваться изучением ограниченной выборочной совокупности.
Определение: Выборочной совокупностью (выборкой) называется совокупность объектов, случайно отобранных из генеральной совокупности. Выборочную совокупность можно интерпретировать как подмножество A универсального множества U (рис. 1).
Слайд 5
Продолжение …
Рис. 1.
Требование: Для того, чтобы по данным
выборки можно было уверенно судить о всей генеральной совокупности,
выборка должна быть репрезентативной (представительной). В силу закона больших чисел, выборка будет репрезентативной при выполнении следующих условий:
Объем выборки достаточно велик;
Обеспечена случайность отбора объектов совокупности;
Обеспечена равная вероятность попадания в выборку любого объекта генеральной совокупности.
Слайд 6
Продолжение …
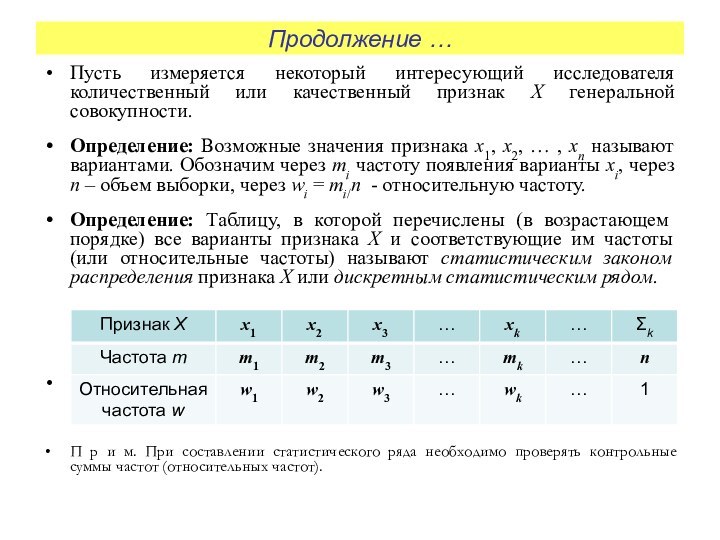
Пусть измеряется некоторый интересующий исследователя количественный или
качественный признак X генеральной совокупности.
Определение: Возможные значения признака
x1, x2, … , xn называют вариантами. Обозначим через mi частоту появления варианты xi, через n – объем выборки, через wi = mi/n - относительную частоту.
Определение: Таблицу, в которой перечислены (в возрастающем порядке) все варианты признака X и соответствующие им частоты (или относительные частоты) называют статистическим законом распределения признака X или дискретным статистическим рядом.
П р и м. При составлении статистического ряда необходимо проверять контрольные суммы частот (относительных частот).
Слайд 7
Продолжение …
Определение: Интервальным называется статистический ряд, в котором
значения признака отнесены к одному из непересекающихся промежутков, покрывающих
в совокупности весь диапазон возможных значений признака.
П р и м е р 1. Проведено измерение роста x (см) группы учащихся в n = 32 чел. «Сырые» результаты измерений таковы: 152, 160, 174, 177, 148, 149, 151, 178, 163, 170, 172, 152, 167, 171, 163, 156, 154, 168, 173, 145, 168, 155, 154, 153, 169, 144, 168, 173, 157, 172, 167, 164. Построить интервальный статистический ряд и частотную гистограмму распределения учащихся по росту.
Рис. 2. Частотная гистограмма
распределения учащихся по росту.
Слайд 8
§1. Статистическое изучение случайной величины. Статистические оценки параметров
распределения.
Слайд 11
§1. Продолжение …. Точечные оценки.
Слайд 12
§1. Продолжение …. Точечные оценки.
Слайд 13
§1. Продолжение …. Точечные оценки.
Слайд 14
§1. Продолжение …. Точечные оценки.
Слайд 15
§2. Точность оценки, доверительная вероятность (надежность). Доверительный интервал.
Определение:

Точечной называют оценку в статистической случайной величины X, которая
определяется одним числом.
Все рассмотренные выше оценки – точечные. Например, точечной оценкой генерального СКО г является исправленное СКО s. Однако точечная оценка не позволяет судить о точности этой оценки. По этой причине предпочтительнее пользоваться интервальными оценками.
Определение: Интервальной называют оценку с.в. X, которая определяется двумя числами – концами интервала, заключающего в себе точечную оценку этой с.в.
Все рассмотренные выше оценки – точечные. Например, точечной оценкой генерального СКО г является исправленное СКО s. Однако точечная оценка не позволяет судить о точности этой оценки. По этой причине предпочтительнее пользоваться интервальными оценками.
Пусть найденная по данным выборки величина в служит случайной оценкой неизвестного параметра г генеральной совокупности. Число > 0 служит мерой точности случайной оценки, если |г в| < . Однако случайный характер выборочной оценки в не позволяет утверждать, что неравенство |г в| < выполняется всегда; можно лишь говорить о вероятности осуществления этого неравенства.
Слайд 16
§2. Точность оценки … Продолжение.
Определение: Надежностью (доверительной вероятностью)

оценки г по в называют вероятность , с которой
осуществляется неравенство |г в| < .
Как правило, надежность оценки задается наперед в виде числа, близкого к единице. Стандартными значениями в этом случае являются доверительные вероятности 0,95; 0,99; 0,995.
Пусть вероятность того, что |г в| < , равна . Иными словами,
P(|г в| < ) = P( < г в < ) = P(в < г < в + ) = .
Это соотношение следует понимать так: вероятность того, что интервал (в ; в + ) заключает в себе (покрывает) оцениваемый неизвестный параметр г, равна .
Определение: Доверительным называют интервал (в ; в + ), который покрывает оцениваемый неизвестный параметр г генеральной совокупности с заданной надежностью .
З а м е ч а н и е: В силу случайного характера оценки г по в, концы интервала (в ; в + ) сами являются случайными числами (их называют доверительными границами).
Метод доверительных интервалов разработал американский статистик Ю. Нейман, развивая идеи английского статистика Р. Фишера.
Слайд 17
§2. Точность оценки … Доверительные интервалы для оценки
математического ожидания нормального распределения при известном .
Слайд 18
§2. Точность оценки … Продолжение.
Слайд 19
§2. Точность оценки … Продолжение.
Слайд 20
§2. Точность оценки … Продолжение.
Слайд 21
§2. Точность оценки … Продолжение.
Слайд 22
§2. Точность оценки … Доверительные интервалы для оценки
математического ожидания нормального распределения при неизвестном .
Слайд 23
§2. Точность оценки … Продолжение..
Слайд 24
§2. Точность оценки … Продолжение…
Слайд 25
§2. Точность оценки … Оценка истинного значения измеряемой
величины
Постановка задачи. Пусть производится n независимых равноточных измерений некоторой
физической величины X, истинное значение которой неизвестно. Будем рассматривать результаты отдельных измерений как случайные величины X1, X2, …, Xn. Эти величины:
независимы (ибо измерения независимы);
имеют одно и то же математическое ожидание a (истинное значение измеряемой величины – ибо величины X1, X2, …, Xn взяты из одной генеральной совокупности);
имеют одинаковые дисперсии 2 (по той же причине, что и a);
В силу сказанного, можно непосредственно применить результаты решения предшествующей задачи.
П р и м е р 5. Баллы X за ЕГЭ по математике группы абитуриентов объемом n = 366 чел. сгруппированы c 5-балльным шагом. Предполагая, что распределение нормально, оценить математическое ожидание с.в. X и доверительный интервал для него с надежностью = 0,95. Сравнить визуально эмпирическое и расчетное распределения.
Слайд 26
§2. Точность оценки … Продолжение
Слайд 27
Приложение 1. Распределение Стьюдента
Слайд 28
Приложение 1. Распределение Стьюдента. Продолжение
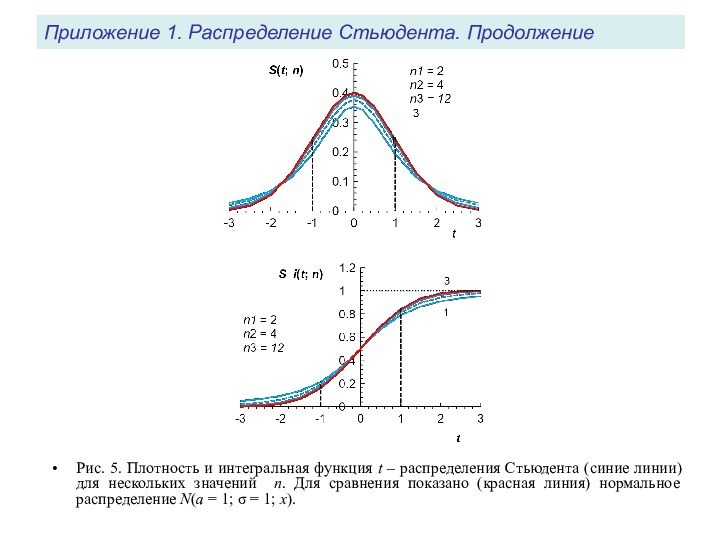
Рис. 5. Плотность и
интегральная функция t – распределения Стьюдента (синие линии) для
нескольких значений n. Для сравнения показано (красная линия) нормальное распределение N(a = 1; = 1; x).
Слайд 29
Приложение 2. William Sealy Gosset
Уи́льям Си́ли Го́ссет (13
июня 1876 г. — 16 октября 1937 г.) —
известный учёный-статистик, более известный под своим псевдонимом Стьюдент и за свои работы по исследованию т.н. Распределения Стьюдента.
Слайд 30
Приложение 2. William Sealy Gosset. Продолжение
Родился в Кентербери,

у Агнес Сили Видал и полковника Фредерика Госсета. Госсет
посещал колледж Винчестер (англ.), а затем прослушал курсы химии и математики в Новом колледже Оксфорда. По окончании университета в 1899 году он поступил на работу на пивоваренный завод Arthur Guinness Son & Co в Дублине.
«Гиннесс» был передовым предприятием пищевой промышленности, и Госсет мог применить свои знания в области статистики как при варке пива, так и на полях — для выведения самого урожайного сорта ячменя. Госсет приобретал эти знания путём изучения, методом проб и ошибок, проведя два года (1906—1907 гг.) в биометрической лаборатории Карла Пирсона. Госсет и Пирсон были в хороших отношениях, и Пирсон помогал Госсету в математической части его исследований. Так, Пирсон был причастен к публикациям 1908 года (принёсших славу Стьюденту), но придавал мало значения этому открытию. Исследования были обращены к нуждам пивоваренной компании и проводились на малом количестве наблюдений. Биометристы же обычно имели дело с сотнями наблюдений и не испытывали необходимости в развитии методов, основанных на малом их количестве.
Ранее другой исследователь, работавший на «Гиннесс», опубликовал в своих материалах сведения, составлявшие коммерческую тайну этой пивоваренной компании. Чтобы предотвратить дальнейшее раскрытие конфиденциальной информации, «Гиннесс» запретил своим работникам публикацию любых материалов, независимо от содержавшейся в них информации. Это означало, что Госсет не мог опубликовать свои работы под своим именем. Поэтому он избрал себе псевдоним Стьюдент, чтобы скрыть себя от работодателя. Поэтому его самое важное открытие получило название Распределение Стьюдента, иначе бы оно могло называться теперь распределением Госсета.
Слайд 31
Приложение 2. William Sealy Gosset. Продолжение
Госсет практически все

свои работы, включая работу «Вероятная ошибка среднего» (англ. The
probable error of a mean) опубликовал в журнале Пирсона «Биометрика» под псевдонимом Стьюдент. Первым, кто понял значение работ Госсета по оценке параметров малой выборки, был биолог Рональд Фишер. Госсет написал ему: «Я посылаю вам копию таблиц Стьюдента, поскольку вы, похоже, единственный человек, который когда-либо станет пользоваться ими!» Фишер считал, что Госсет совершил «логическую революцию». По иронии судьбы, t - статистика, благодаря которой знаменит Госсет, была фактически изобретением Фишера. Госсет считал статистику для z = t /√(n1). Фишер предложил вычислять статистику для t, потому что такое представление укладывалось в его теорию степеней свободы. Фишер также применил распределение Стьюдента в регрессионном анализе.
Стьюдентизированные остатки также названы в честь Стьюдента, хотя их предложили другие учёные. Подобно проблемам, которые привели к распределению Стьюдента, в их основе лежит та же идея — исправление (adjusting) выборочного стандартного отклонения. Интерес Госсета к выращиванию ячменя привёл его к мысли, что опыт надо планировать с той целью, чтобы не просто повысить среднюю урожайность, но чтобы вывести такие сорта ячменя, чья урожайность была бы устойчива к колебаниям состава почвы или климата. Этот принцип встречается только позднее у Фишера и затем в 1950-х в работе Гэнъити Тагути.
В 1935 году он покинул Дублин, чтобы занять должность главного пивовара, ответственного за научную сторону производственного процесса, в новой пивоварне Гиннесса в Парк Ройял (англ.), в северо-западной части Лондона. Он скончался от сердечного приступа в городе Беконсфильд (англ.) в Англии.
Госсет был другом Пирсона и Фишера и был достаточно скромным человеком. Известен случай, когда он оборвал речь своего почитателя словами «Фишер всё равно бы сумел открыть всё это сам».
Слайд 32
§3. Элементы корреляционного анализа. Функциональная, статистическая и корреляционная

зависимости
Во многих задачах требуется установить наличие и оценить степень
зависимости изучаемой величины Y от одной или нескольких других случайных величин X (или X1, X2, …, Xn). Прежде всего, рассмотрим зависимость с.в. Y от одной случайной или неслучайной величины X.
Две с.в. Y и X могут быть: а) связаны функционально; б) связаны статистической, в частности, корреляционной зависимостью; в) независимы.
Определение: Статистической называют зависимость, при которой изменение одной из величин влечет изменение распределения другой. Если, при этом, изменение одной из величин влечет изменение среднего значения другой, то такую статистическую зависимость называют корреляционной.
П р и м е р 6. Пусть с.в. Y – урожай зерна; с.в. X – количество внесенных удобрений. С одинаковых по площади участков снимают различный урожай, т.е. Y не является функцией X, ибо на величину урожая, помимо количества удобрений, влияет множество случайных факторов (осадки, температура воздуха, качество почвы и др.). Вместе с тем, как показывает опыт, средний урожай определенно зависит от количества внесенных удобрений. Иными словами с.в. Y и X связаны корреляционной зависимостью.
Слайд 33
§3. Элементы корреляционного анализа. Отыскание параметров выборочного уравнения
прямой линии среднеквадратической регрессии.
Пусть изучается система количественных признаков (X;
Y). В результате n независимых опытов получены n пар чисел (x1; y1), (x2; y2), …, (xn; yn).
Найдем по данным наблюдений выборочное уравнение прямой линии среднеквадратичной регрессии. Уравнение будем искать в виде регрессии Y на X:
y = kx + b,
где угловой коэффициент k называют выборочным коэффициентом регрессии Y на X и обычно обозначают yx.
Определение: Выборочным уравнением линейной регрессии Y на X называют уравнение вида
Y = yx x + b,
наилучшим образом (в определенном смысле) описывающее n пар чисел (x1; y1), (x2; y2), …, (xn; yn).
Определение: Назовем отклонением разность Yi yi, i = 1, 2, …, n. Здесь Yi расчетная по уравнению регрессии ордината, соответствующая абсциссе xi, yi экспериментальная i-ая ордината.
Слайд 34
§3. Элементы корреляционного анализа. Продолжение...
Слайд 35
§3. Элементы корреляционного анализа. Продолжение...
П р и м
е р 7. Найти выборочное уравнение прямой линии регрессии
Y на X по данным n = 5 наблюдений:
Решение: Составим расчетную таблицу и вычислим yx и b:
yx = (526,975 158,15)/(557,5152) = 0,202;
b = (57,58,15 1526,975)/(557,5152) = 1,024.
Слайд 36
§3. Элементы корреляционного анализа. Продолжение...
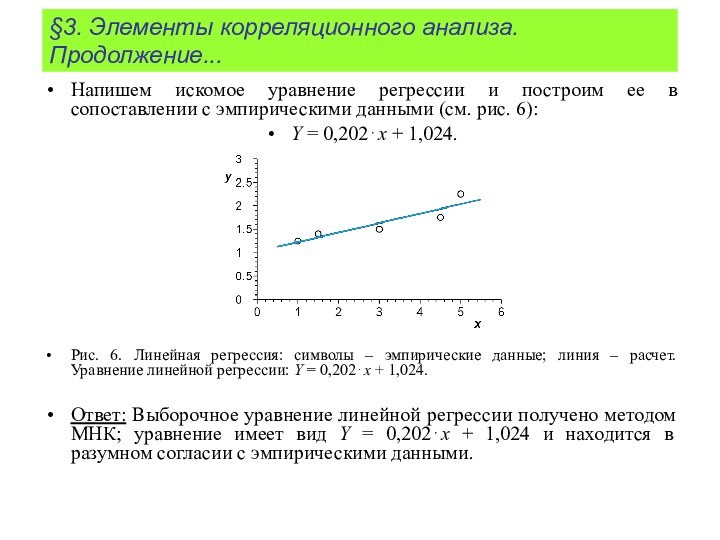
Напишем искомое уравнение регрессии
и построим ее в сопоставлении с эмпирическими данными (см.
рис. 6):
Y = 0,202x + 1,024.
Рис. 6. Линейная регрессия: символы – эмпирические данные; линия – расчет. Уравнение линейной регрессии: Y = 0,202x + 1,024.
Ответ: Выборочное уравнение линейной регрессии получено методом МНК; уравнение имеет вид Y = 0,202x + 1,024 и находится в разумном согласии с эмпирическими данными.
Слайд 37
§3. Элементы корреляционного анализа. Продолжение...
Слайд 38
§3. Элементы корреляционного анализа. Продолжение...