Что такое findslide.org?

FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.

Для правообладателей

Обратная связь

Email: Нажмите что бы посмотреть 

Яндекс.Метрика

Презентация на тему Фигуры в геометрии

Содержание

Не секрет, что порою для решения задачи не хватает знания какой-то одной-единственной формулы, которую хочется быстрее найти и применить, но не всегда эта формула находится под рукой, поэтому в презентации собраны самые важные и
Справочник по геометрии7-9 классМБОУ СОШ с.ВостокАвтор:Чучуй Любовь Анатольевна Не секрет, что порою для решения задачи не хватает знания Цели и задачи создания справочника:систематизировать материал по основным математическим понятиям и формулам Треугольник ТреугольникАСВbса Свойства равнобедренного треугольникаВ равнобедренном треугольнике углы при основании равныМедиана, проведенная к основанию Признаки равенства треугольниковСУСУСУСССПо двум сторонам и углу между нимиПо стороне и двум Признаки равенства прямоугольных треугольников Свойства прямоугольного треугольникаВ прямоугольном треугольнике сумма острых углов равна 90°. СВАСоотношения между сторонами и углами треугольникаВ треугольнике АВD:против большего угла лежит большая Признаки подобия треугольников h = с2 =а2+b2Теорема: В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетовТеорема ПифагораОбратная Признаки параллельности прямых Параллелограммом называется четырехугольник, у которого противоположные стороны попарно параллельныDАВС(АB || CD,BC || DАВСПараллелограммО Квадрат - это прямоугольник, у которого все стороны равны.ааКвадратКвадрат обладает всеми свойствами Прямоугольником называется параллелограмм, у которого все углы прямыеПрямоугольникАODСВДиагонали прямоугольника равны ПрямоугольникАODСВОсновные формулыab Все стороны ромба равны АВ=ВС=СД=ДА. Противолежащие углы ромба равныДиагонали АВСDОРомбРомбом называется параллелограмм, у которого все стороны равныОсновные формулыAВ = BС = Четырехугольник, у которого две стороны параллельны, а две другие нет, называется трапецией.ABCDBC, Соотношения между сторонами и углами в прямоугольном треугольникеаbсАВСПротиволежащий катетПрилежащий катет Гипотенуза-основное тригонометрическое ОкружностьОАОА - радиус окружности (r);СВ - диаметр окружности (d);MN – хорда окружности; ОкружностьОсновные формулыd = 2rC = 2πr – длина окружностиS = πr2 – площадь кругаrАВО Федеральный компонент государственного образовательного стандарта основного общего образования по математике (пр.министерства образования
Слайды презентации

Слайд 2 Не секрет, что порою для решения

Не секрет, что порою для решения задачи не хватает знания

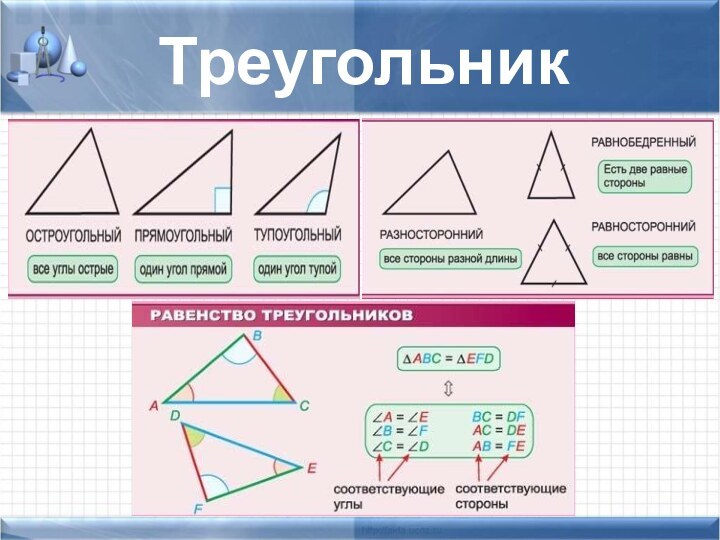
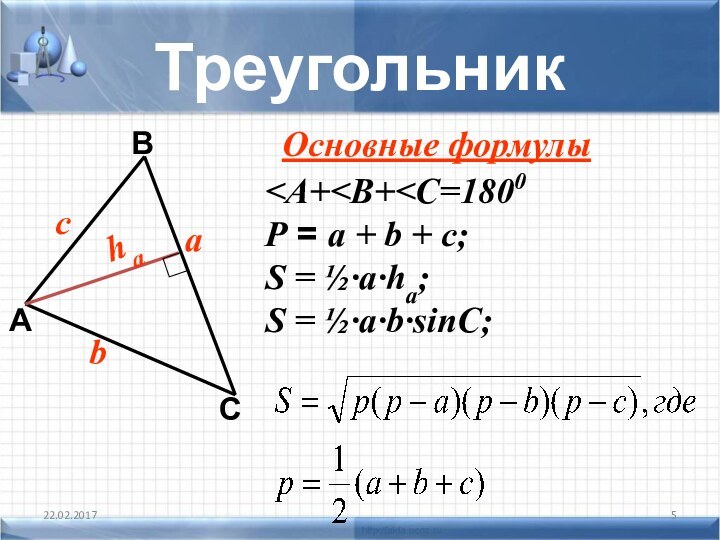
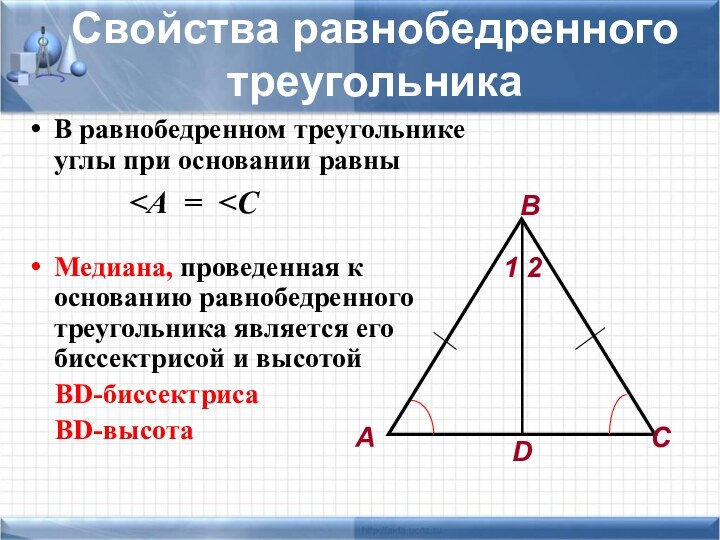
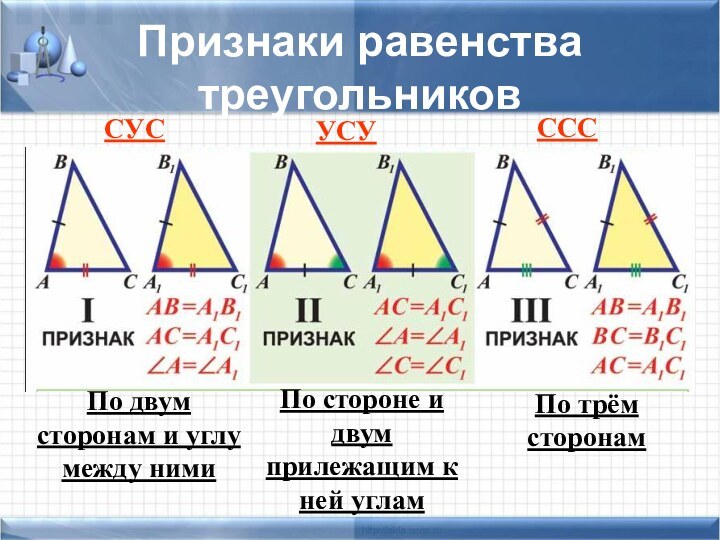
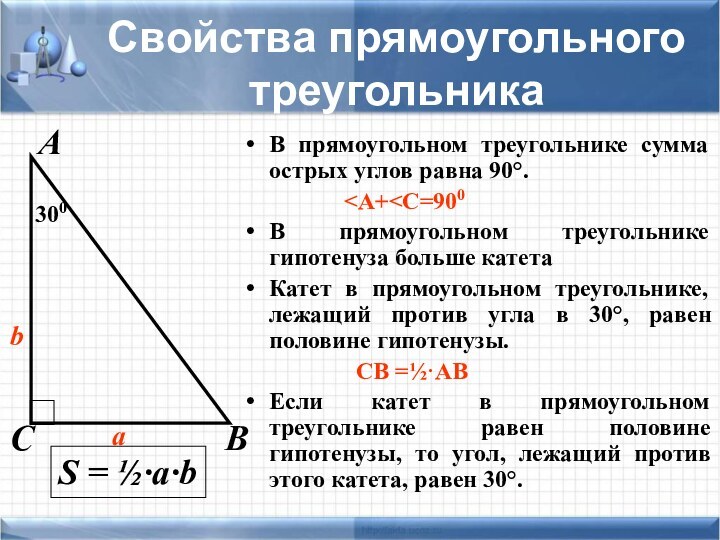
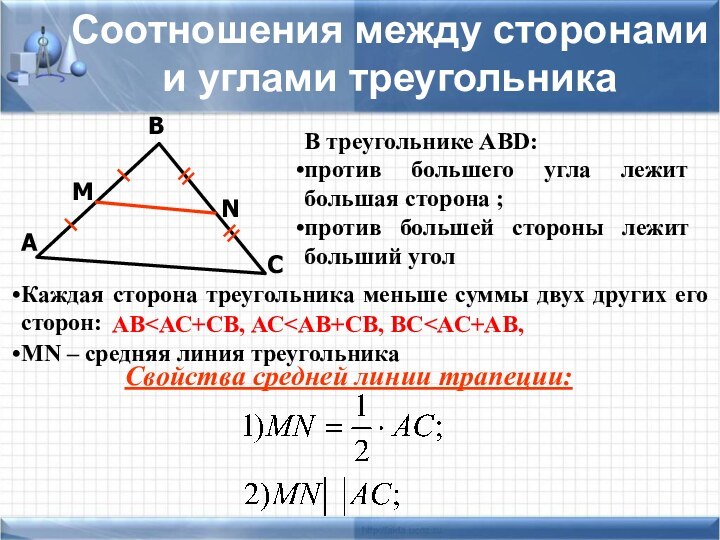
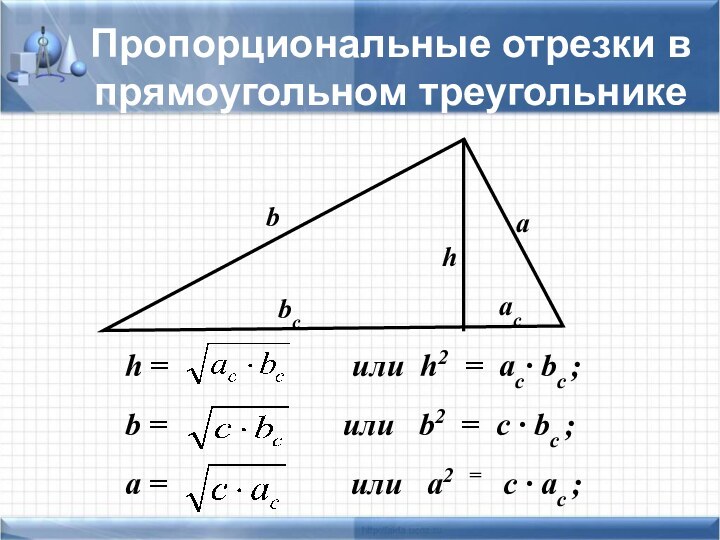
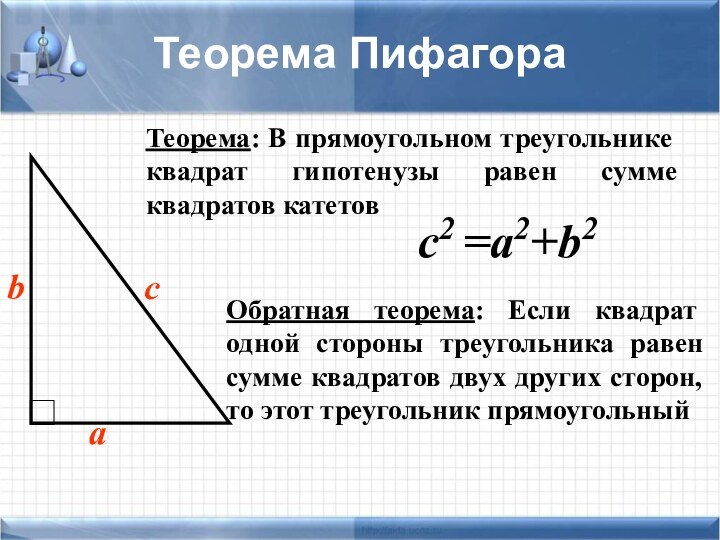
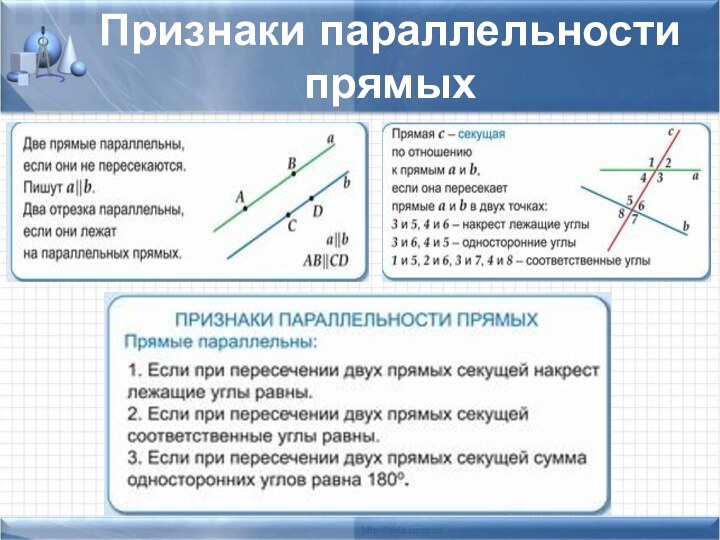
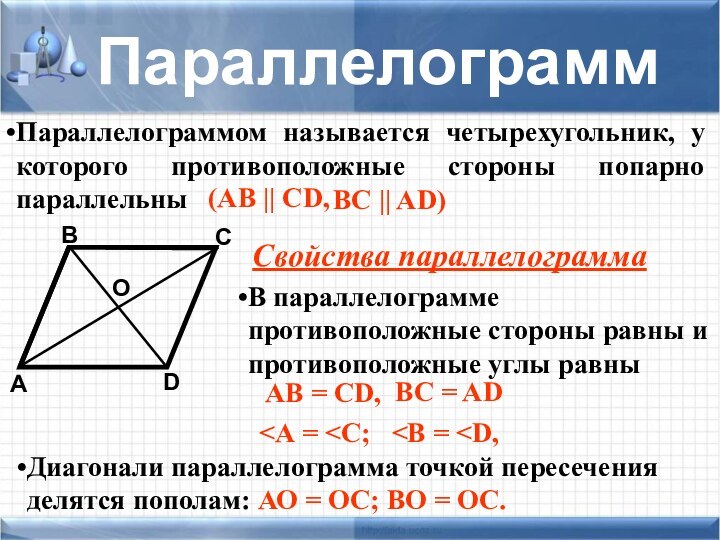
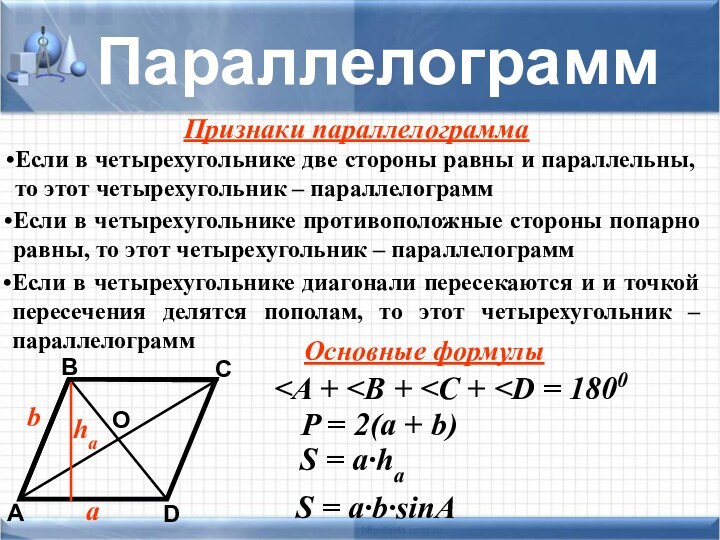
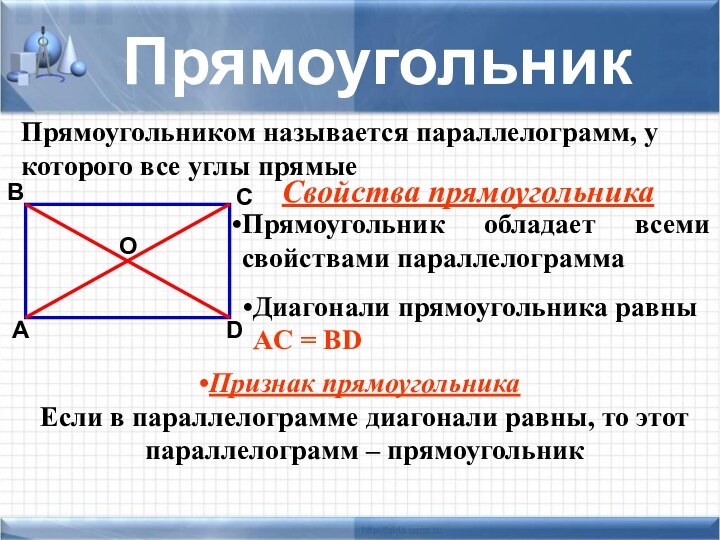
задачи не хватает знания какой-то одной-единственной формулы, которую хочется

быстрее найти и применить, но не всегда эта формула находится под рукой, поэтому в презентации собраны самые важные и нужные формулы геометрии, которые могут пригодиться при решении различных заданий.
Важную роль играет использование математического справочника при самоподготовке к ЕГЭ в 11 классе и ГИА в 9 классе.
Создание справочника не закончено. Собраны основные формулы по курсу геометрии 7-9 классов. Работа над созданием справочника продолжается

Номинация: интерактивная презентация к урокам

Слайд 3 Цели и задачи создания справочника:
систематизировать материал по основным

Цели и задачи создания справочника:систематизировать материал по основным математическим понятиям и

математическим понятиям и формулам школьного курса геометрии;
создать учащимся

условия для беспроблемного решения многих математических задач при выполнении домашнего задания, при подготовке к контрольным и самостоятельным работам, к ЕГЭ и ГИА;
способствовать развитию познавательной активности учащихся через знакомство с формулами, облегчающими процесс решения задачи;
способствовать развитию математических способностей одарённых детей через знакомство с формулами, не входящими в школьную программу по математике.

Слайд 4 Треугольник

Треугольник

Слайд 5 Треугольник
А
С
В
b
с
а

ТреугольникАСВbса

½·a·ha;
S = ½·a·b·sinC;
ha
Основные формулы

Слайд 6 Свойства равнобедренного треугольника
В равнобедренном треугольнике углы при основании

Свойства равнобедренного треугольникаВ равнобедренном треугольнике углы при основании равныМедиана, проведенная к

равны


Медиана, проведенная к основанию равнобедренного треугольника является его биссектрисой

и высотой
ВD-биссектриса
ВD-высота

А

В

С

<А = <С

D

1

2

Слайд 7 Признаки равенства треугольников
СУС
УСУ
ССС
По двум сторонам и углу между

Признаки равенства треугольниковСУСУСУСССПо двум сторонам и углу между нимиПо стороне и

ними
По стороне и двум прилежащим к ней углам
По трём

сторонам

Слайд 8 Признаки равенства прямоугольных треугольников

Признаки равенства прямоугольных треугольников

Слайд 9 Свойства прямоугольного треугольника
В прямоугольном треугольнике сумма острых углов

Свойства прямоугольного треугольникаВ прямоугольном треугольнике сумма острых углов равна 90°.

равна 90°.

В прямоугольном треугольнике гипотенуза больше катета
Катет в прямоугольном треугольнике, лежащий против угла в 30°, равен половине гипотенузы.
CB =½·AB
Если катет в прямоугольном треугольнике равен половине гипотенузы, то угол, лежащий против этого катета, равен 30°.

A

B

C

300

a

b

S = ½·a·b

Слайд 10 С
В
А
Соотношения между сторонами и углами треугольника
В треугольнике АВD:
против

СВАСоотношения между сторонами и углами треугольникаВ треугольнике АВD:против большего угла лежит

большего угла лежит большая сторона ;
против большей стороны лежит

больший угол

АВ<АС+СВ, АС<АВ+СВ, ВС<АС+АВ,

Каждая сторона треугольника меньше суммы двух других его сторон:

M

N

MN – средняя линия треугольника

Свойства средней линии трапеции:

Слайд 11 Признаки подобия треугольников

Признаки подобия треугольников

Слайд 12 h =

h = или

или h2 = ac· bc ;

b = или b2 = c · bc ;

a = или a2 = c · ac ;

b

a

h

bc

ac

Пропорциональные отрезки в прямоугольном треугольнике

Слайд 13 с2 =а2+b2
Теорема: В прямоугольном треугольнике квадрат гипотенузы равен

с2 =а2+b2Теорема: В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетовТеорема

сумме квадратов катетов
Теорема Пифагора
Обратная теорема: Если квадрат одной стороны

треугольника равен сумме квадратов двух других сторон, то этот треугольник прямоугольный

Слайд 14 Признаки параллельности прямых

Признаки параллельности прямых

Слайд 15 Параллелограммом называется четырехугольник, у которого противоположные стороны попарно

Параллелограммом называется четырехугольник, у которого противоположные стороны попарно параллельныDАВС(АB || CD,BC

параллельны
D
А
В
С
(АB || CD,
BC || AD)
Параллелограмм
В параллелограмме противоположные стороны равны

и противоположные углы равны

Диагонали параллелограмма точкой пересечения делятся пополам: АО = ОС; ВО = ОС.

АB = CD,

BC = AD

<А = <С;

О

Свойства параллелограмма

Слайд 16 D
А
В
С
Параллелограмм
О

DАВСПараллелограммО

1800
a
b
P = 2(a + b)
S = a·ha
ha
S = a·b·sinA
Признаки

параллелограмма
Если в четырехугольнике две стороны равны и параллельны, то этот четырехугольник – параллелограмм

Если в четырехугольнике противоположные стороны попарно равны, то этот четырехугольник – параллелограмм

Если в четырехугольнике диагонали пересекаются и и точкой пересечения делятся пополам, то этот четырехугольник – параллелограмм

Основные формулы

Слайд 17 Квадрат - это прямоугольник, у которого все стороны

Квадрат - это прямоугольник, у которого все стороны равны.ааКвадратКвадрат обладает всеми

равны.
а
а
Квадрат
Квадрат обладает всеми свойствами и признаками параллелограмма, прямоугольника, ромба
Основные

формулы

А

D

С

В

P = 4a

S = a2

S = ½·P·r
(r-радиус вписанной окружности)

(R-радиус описанной окружности)

Слайд 18 Прямоугольником называется параллелограмм, у которого все углы прямые
Прямоугольник
А
O
D
С
В
Диагонали

Прямоугольником называется параллелограмм, у которого все углы прямыеПрямоугольникАODСВДиагонали прямоугольника равны

прямоугольника равны AC = BD
Признак прямоугольника Если

в параллелограмме диагонали равны, то этот параллелограмм – прямоугольник

Свойства прямоугольника

Прямоугольник обладает всеми свойствами параллелограмма

Слайд 19 Прямоугольник
А
O
D
С
В
Основные формулы
a
b

ПрямоугольникАODСВОсновные формулыab

= 900
P = 2(a + b)
S = a·b
Прямоугольником называется

параллелограмм, у которого все углы прямые

Слайд 20 Все стороны ромба равны
АВ=ВС=СД=ДА.

Все стороны ромба равны АВ=ВС=СД=ДА. Противолежащие углы ромба равныДиагонали ромба

Противолежащие углы ромба равны
Диагонали ромба точкой пересечения делятся пополам:

АО=ОС, ВО=ОД.
Диагонали ромба взаимно перпендикулярны АС ВД.
Диагонали ромба являются биссектрисами его углов

А

В

С

D

О

Ромб

Ромбом называется параллелограмм, у которого все стороны равны

Свойства ромба

Слайд 21 А
В
С
D
О
Ромб
Ромбом называется параллелограмм, у которого все стороны равны
Основные

АВСDОРомбРомбом называется параллелограмм, у которого все стороны равныОсновные формулыAВ = BС

формулы
AВ = BС = CD = AD = a
P

= 4a

a

d1

d2

S = ½·d1·d2

Слайд 22 Четырехугольник, у которого две стороны параллельны, а две

Четырехугольник, у которого две стороны параллельны, а две другие нет, называется

другие нет, называется трапецией.
A
B
C
D
BC, AD–основания трапеции, ВС║АD
AB,CD –

боковые стороны

Трапеция

M

N

MN –средняя линия трапеции

Свойства
средней линии трапеции:

P = АВ+ВС+СD+AD

Основные формулы

a

b

h

В равнобедренной трапеции углы при основаниях равны

В равнобедренной трапеции диагонали равны

Слайд 23 Соотношения между сторонами и углами в прямоугольном треугольнике
а
b
с
А
В
С
Противолежащий

Соотношения между сторонами и углами в прямоугольном треугольникеаbсАВСПротиволежащий катетПрилежащий катет Гипотенуза-основное

катет
Прилежащий катет
Гипотенуза
-основное тригонометрическое
тождество
Таблица значений sinα, cosα, tgα

для некоторых углов

Слайд 24 Окружность
О
А
ОА - радиус окружности (r);
СВ - диаметр окружности

ОкружностьОАОА - радиус окружности (r);СВ - диаметр окружности (d);MN – хорда

(d);
MN – хорда окружности;
АС – дуга окружности;
РК

– касательная к окружности

С

В

М

N

Р

К

Касательная к окружности перпендикулярна к радиусу, проведённому в точку касания:
ОА РК

Отрезки касательных к окружности, проведённые из одной точки, равны (АВ=АС) и составляют равные углы с прямой, проходящей через эту точку и центр окружности (<ВАО = <САО)

d = 2r

Слайд 25 Окружность
Основные формулы
d = 2r
C = 2πr – длина

ОкружностьОсновные формулыd = 2rC = 2πr – длина окружностиS = πr2 – площадь кругаrАВО

окружности
S = πr2 – площадь круга
r
А
В
О

= АВ ( АВ < полуокружности)
(

А

В

О

С

<ВАС – вписанный угол
<ВАС = ½ ВС
Вписанный угол, опирающийся на
полуокружность - прямой

  • Имя файла: figury-v-geometrii.pptx
  • Количество просмотров: 131
  • Количество скачиваний: 0
- Предыдущая Имидж учителя
Следующая - Ассортимент швейных изделий

Похожие презентации

Математика. 1 класс. Урок 75. Длина. Дециметр - Презентация презентация к уроку по математике (1 класс) по теме Математика. 1 класс. Урок 75. Длина. Дециметр - Презентация презентация к уроку по математике (1 класс) по теме 131
Слайды к занятию презентация урока для интерактивной доски по математике (средняя группа) Слайды к занятию презентация урока для интерактивной доски по математике (средняя группа) 117
Метр. Соотношение единиц длины Метр. Соотношение единиц длины 100
1 - 1 1 - 1 95
Задания №15 базового уровня (прямоугольник) Задания №15 базового уровня (прямоугольник) 117
Блок-схема для решения квадратных неравенств Блок-схема для решения квадратных неравенств 88
Задачи на перебор вариантов. Ознакомление с решением задач путём составления таблиц. презентация к уроку по математике (4 класс) Задачи на перебор вариантов. Ознакомление с решением задач путём составления таблиц. презентация к уроку по математике (4 класс) 190
Презентация Связь между компонентами сложения 1 класс презентация к уроку по математике (1 класс) по теме Презентация Связь между компонентами сложения 1 класс презентация к уроку по математике (1 класс) по теме 103
Дозирование жидких лекарственных форм Дозирование жидких лекарственных форм 135
Презентация Математика и физика в хокее Презентация Математика и физика в хокее 146
Число 1, цифра 1. презентация к уроку по математике (1 класс) Число 1, цифра 1. презентация к уроку по математике (1 класс) 118
Математика. 1 класс. Урок 5. Признаки предметов презентация к уроку по математике (1 класс) по теме Математика. 1 класс. Урок 5. Признаки предметов презентация к уроку по математике (1 класс) по теме 131
Методи математичного моделювання на прикладі бізнес – плану Методи математичного моделювання на прикладі бізнес – плану 187
Презентация к уроку математики по теме Прямоугольный параллелепипед Презентация к уроку математики по теме Прямоугольный параллелепипед 90
doktor aybolit prezentatsiya slayd 1 doktor aybolit prezentatsiya slayd 1 102
Тест по математике. 4 класс. презентация к уроку по математике (4 класс) Тест по математике. 4 класс. презентация к уроку по математике (4 класс) 167
Математика в профессиях Математика в профессиях 152
Учимся считать на пальцах Учимся считать на пальцах 98
Урок математики в 4 классе по теме : Понятие о действии возведения в степень план-конспект урока по математике (4 класс) Урок математики в 4 классе по теме : Понятие о действии возведения в степень план-конспект урока по математике (4 класс) 105
Игра как эффективная форма развития познавательного интереса учащихся к математике Игра как эффективная форма развития познавательного интереса учащихся к математике 85
Синус, косинус, тангенс угла Синус, косинус, тангенс угла 122
Презентация по теме Решение несложных логических задач 5 класс Презентация по теме Решение несложных логических задач 5 класс 128
Показательная функция Показательная функция 129
Полярные координаты Полярные координаты 171
Дидактические игры на уроках математики Дидактические игры на уроках математики 111
Деловая игра Следствие ведут знатоки Деловая игра Следствие ведут знатоки 127
Конспект НОД Птицы зимой для детей 6-7 лет план-конспект занятия по математике (старшая группа) Конспект НОД Птицы зимой для детей 6-7 лет план-конспект занятия по математике (старшая группа) 192
История возникновения часов История возникновения часов 111
Фотоотчет о неделе математики презентация к уроку по математике Фотоотчет о неделе математики презентация к уроку по математике 113
Урок по теме Проценты Урок по теме Проценты 178