- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Фигуры вращения
Содержание
- 2. Содержание моей презентации:ЦилиндрКонус и усечённый конусШар и сфера
- 3. ЦилиндрОпределение. Тело, которое образуется
- 4. Круговой прямой цилиндр
- 5. Наклонный цилиндрНаклонный цилиндр – цилиндр, образующие которого не перпендикулярны плоскостям его оснований.
- 6. Пусть R – радиус основания; H –
- 7. КонусОпределение: Тело, которое образуется
- 8. Прямой круговой конус
- 9. Если R – радиус основания,
- 10. Усеченный конус Часть конуса, ограниченная
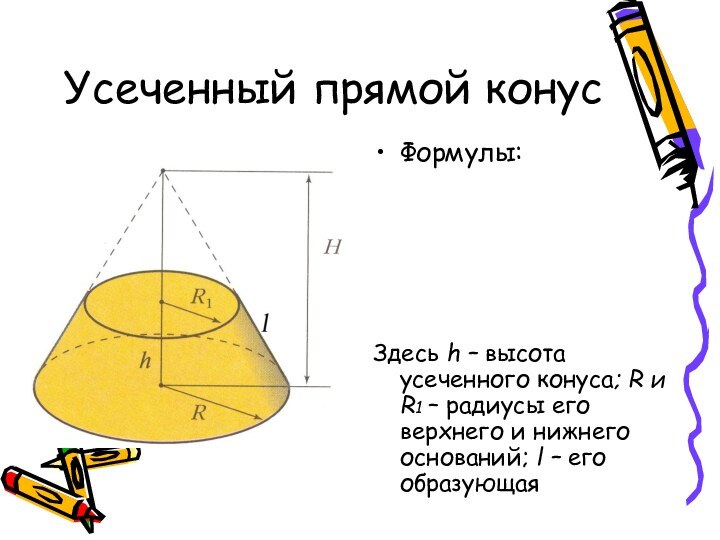
- 11. Усеченный прямой конусФормулы:Здесь h – высота усеченного
- 12. Шар и сфераОпределение.
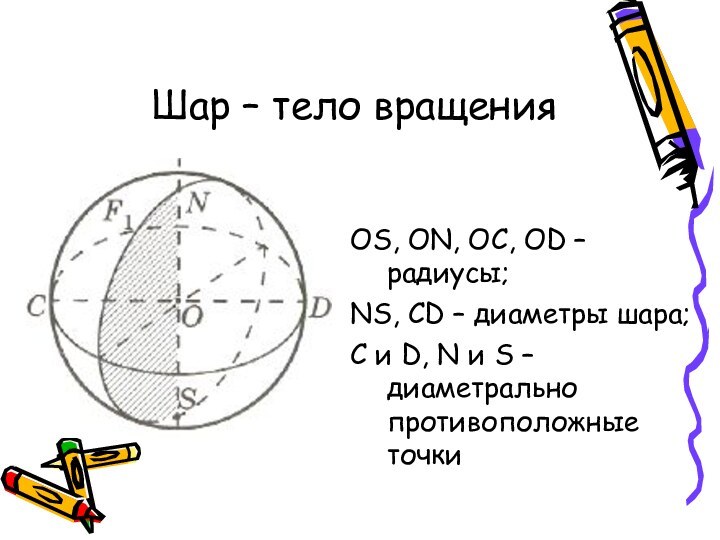
- 13. Шар – тело вращенияOS, ON, OC, OD
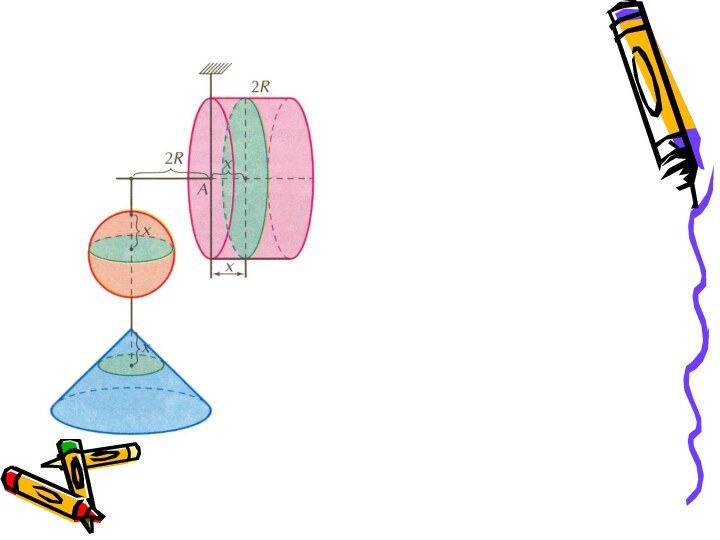
- 14. Как Архимед находил объем шараПлощади сечений: Sц, Sш, Sк.Sц=4πR²;Sш=π[CE]², где [CE]²=[EO]²-[OC]²=R²- -(x-R)²=2Rx-x²;Sк=π[CD]²= πx²
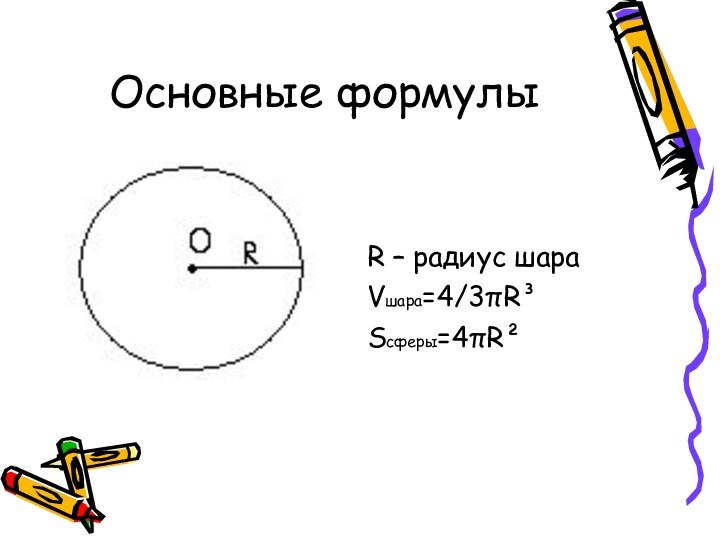
- 16. Основные формулыR – радиус шараVшара=4/3πR³Sсферы=4πR²
- 17. Уравнение сферыПусть A – центр(a; b; c)MA – радиус, тогдаMA²=(x-a)²+(y-b)²+(z-c)²;(x-a)²+(y-b)²+(z-c)²=R²
- 18. Скачать презентацию
- 19. Похожие презентации
Содержание моей презентации:ЦилиндрКонус и усечённый конусШар и сфера








![Фигуры вращения Как Архимед находил объем шараПлощади сечений: Sц, Sш, Sк.Sц=4πR²;Sш=π[CE]², где [CE]²=[EO]²-[OC]²=R²- -(x-R)²=2Rx-x²;Sк=π[CD]²= πx²](/img/tmb/11/1073614/8cb9f4af8b5373a6f1278be103477aa1-720x.jpg)


Слайд 3
Цилиндр
Определение.
Тело, которое образуется при
вращении прямоугольника вокруг прямой, содержащей его сторону, называется цилиндром.
Слайд 5
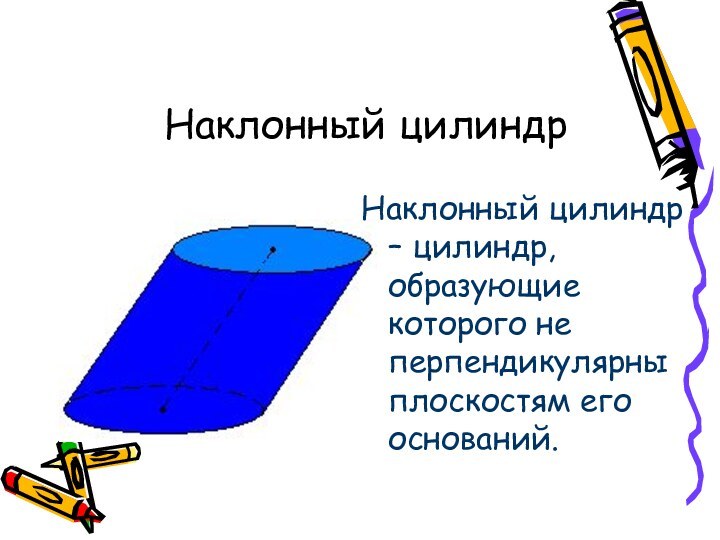
Наклонный цилиндр
Наклонный цилиндр – цилиндр, образующие которого не
перпендикулярны плоскостям его оснований.
Слайд 6
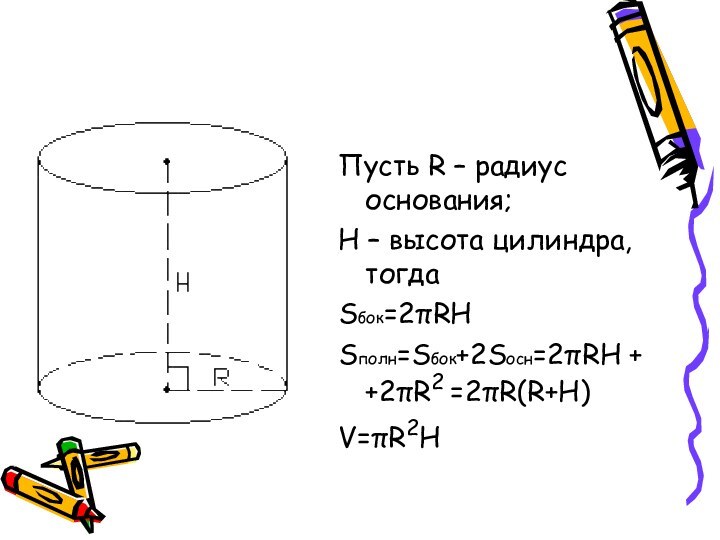
Пусть R – радиус основания;
H – высота
цилиндра, тогда
Sбок=2πRH
Sполн=Sбок+2Sосн=2πRH + +2πR2 =2πR(R+H)
V=πR2H
Основные формулы
Слайд 7
Конус
Определение:
Тело, которое образуется при
вращении прямоугольного треугольника вокруг прямой, содержащий его катет, называется
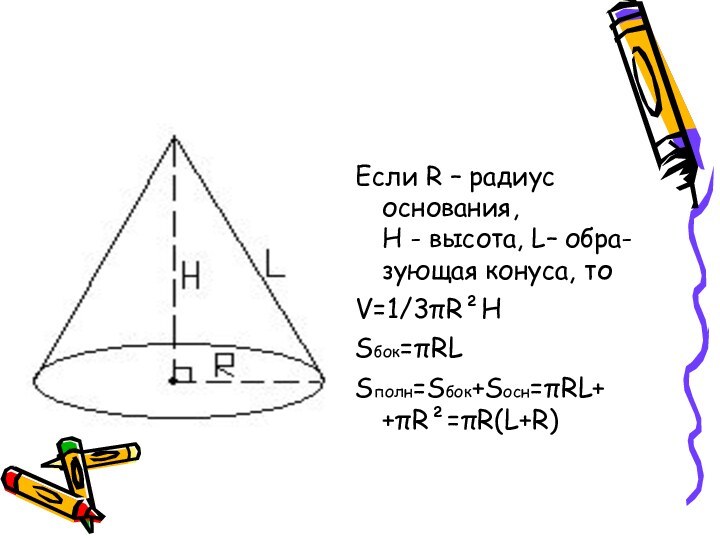
прямым круговым конусом.Слайд 9 Если R – радиус основания,
H - высота, L– обра-
зующая конуса, тоV=1/3πR²H
Sбок=πRL
Sполн=Sбок+Sосн=πRL+ +πR²=πR(L+R)
Основные формулы