- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Формулы для вычисления площадей различных треугольников. 10-й класс
Содержание
- 2. Площадь прямоугольного треугольника.ПЛОЩАДЬ ПРЯМОУГОЛЬНОГО ТРЕУГОЛЬНИКА РАВНА ПОЛОВИНЕПРОИЗВЕДЕНИЯ КАТЕТОВ. АСВDba
- 3. Площадь любого треугольника.АaBCDhaПлощадь любого треугольника равнаполовине произведения основания на высоту.
- 4. Если в треугольнике известны две стороны и
- 5. Площадь треугольника через r-радиус вписанной окружности.Площадь треугольника
- 6. Площадь треугольника через R-радиус описанной окружностиПлощадь треугольника
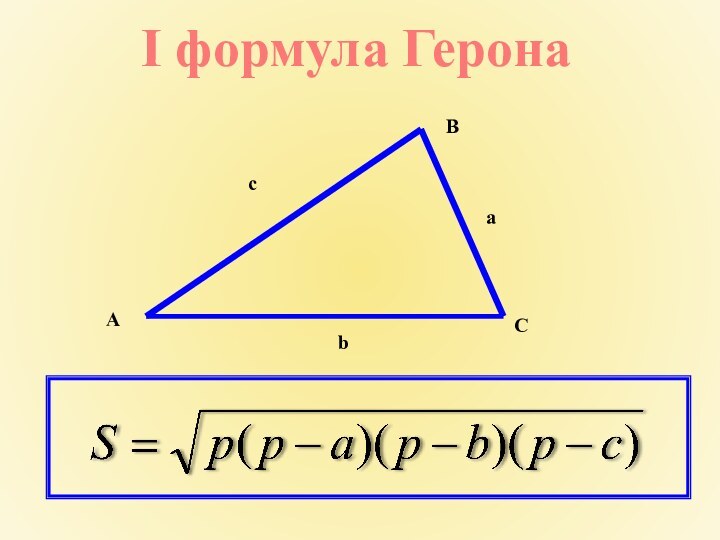
- 7. I формула ГеронаBCAbсa
- 8. Доказательство: По теореме косинусов можно записать:Т.К. точ.т.д.
- 9. ГЕРОН АЛЕКСАНДРИЙСКИЙ (Heronus Alexandrinus)Герон Александрийский – греческий
- 10. II формула Герона BCA
- 11. Итак, мы получили II формулу Герона. И
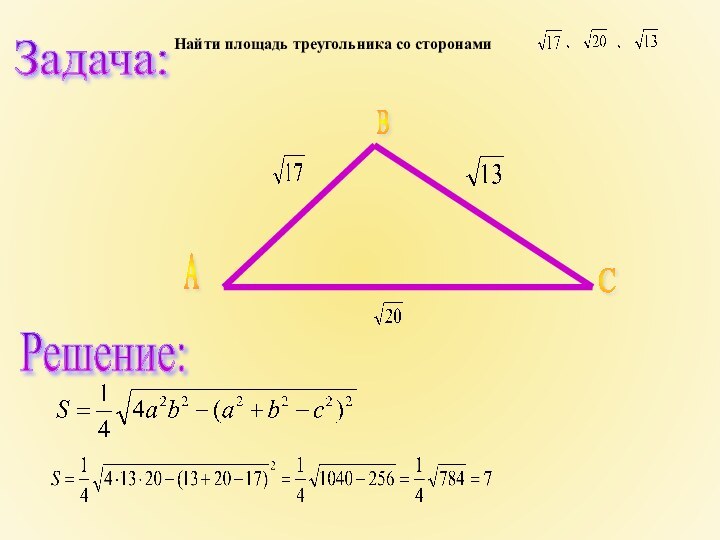
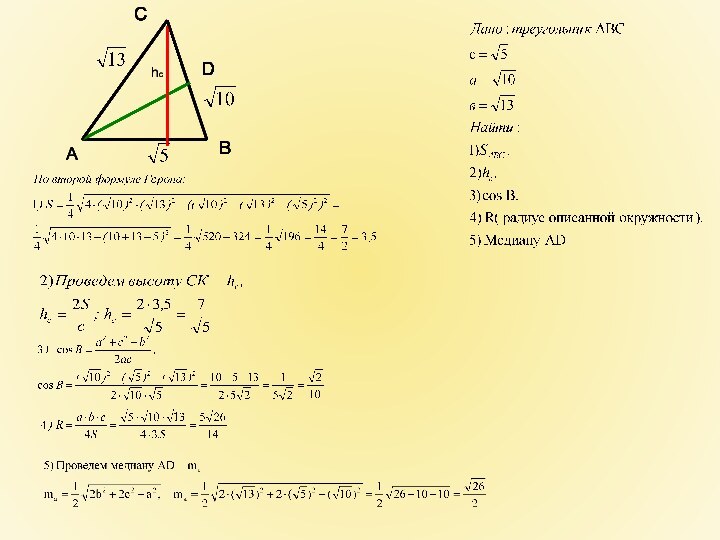
- 12. Найти площадь треугольника со сторонами Решение: Задача: А В С
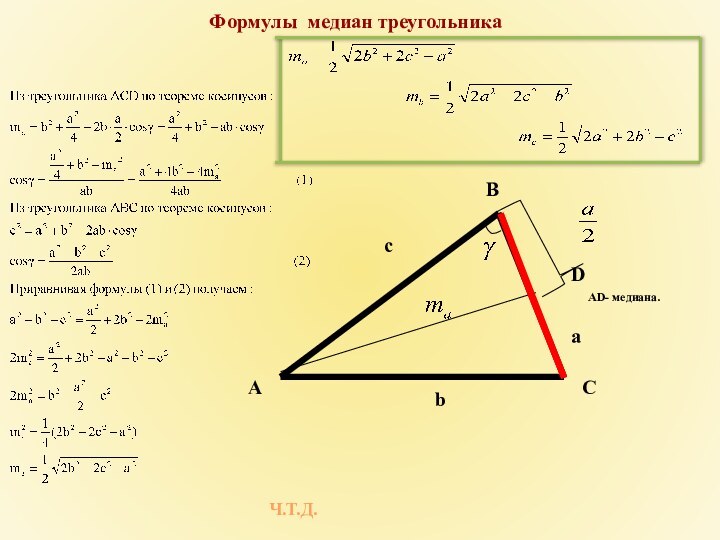
- 13. Формулы медиан треугольникаAD- медиана.Ч.Т.Д.CАBbacD
- 14. CCCCCCCCCCCCDBAhcDDBDBDABDABDCABDhcCABD
- 15. Площадь треугольника в системе координатНайти площадь треугольника
- 16. Если предположить, что х1=у1=0, то получится еще
- 17. Пусть требуется найти площадь S треугольника АВС
- 18. Восемь формул для нахождения площадей различных треугольников.
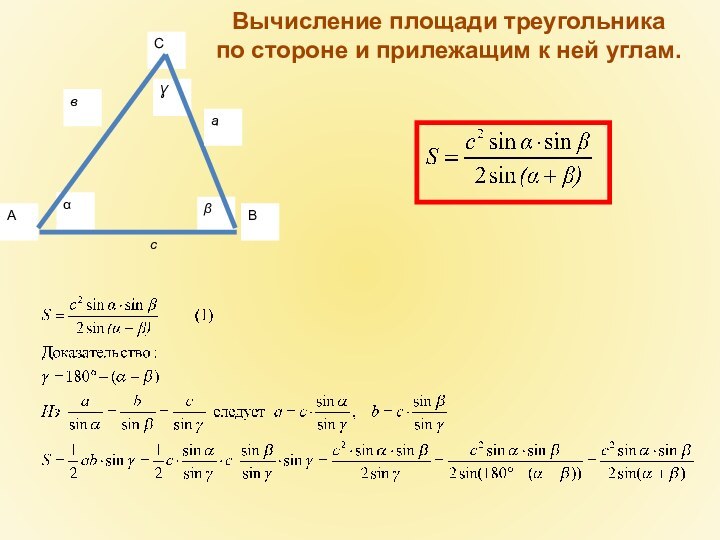
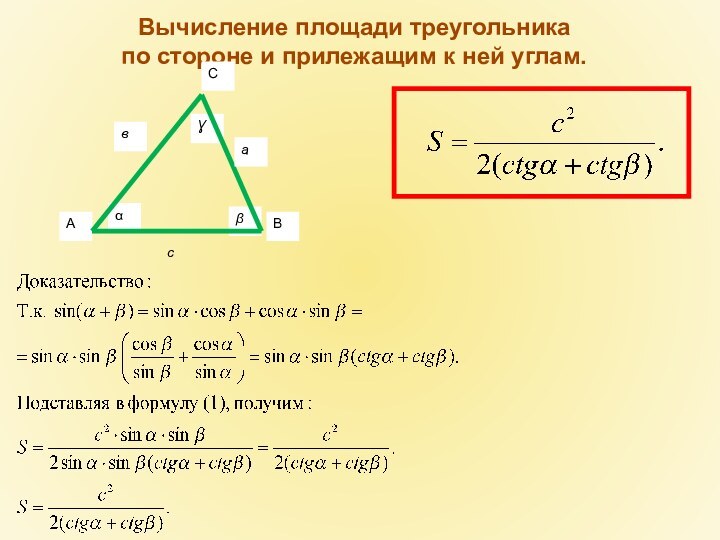
- 19. сВычисление площади треугольникапо стороне и прилежащим к ней углам.
- 20. Вычисление площади треугольникапо стороне и прилежащим к ней углам.
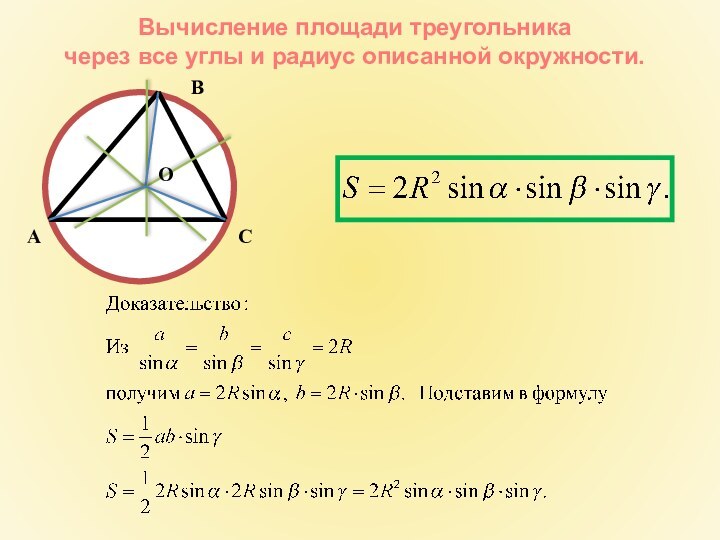
- 21. Вычисление площади треугольника через все углы и радиус описанной окружности.
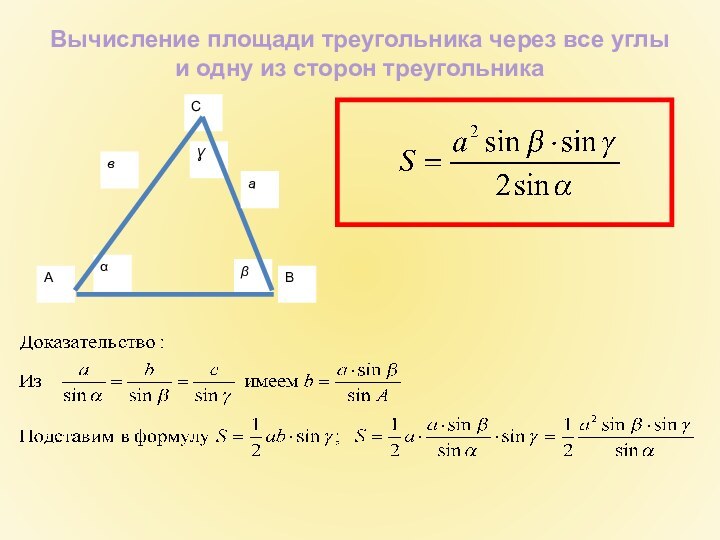
- 22. Вычисление площади треугольника через все углыи одну из сторон треугольника
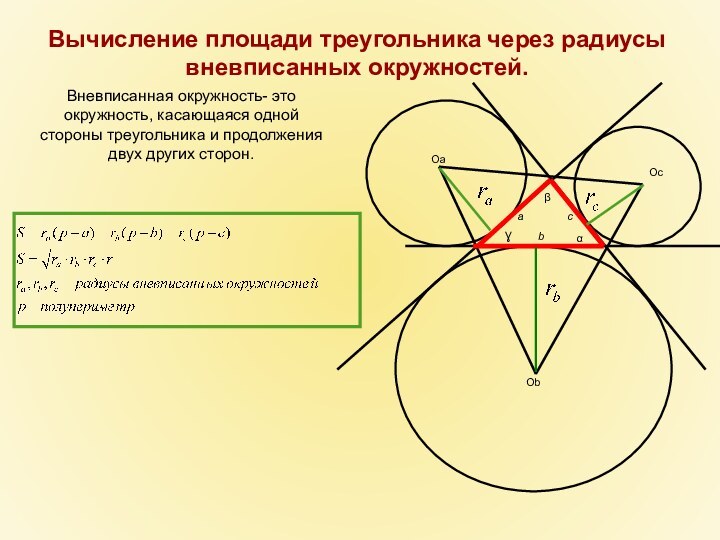
- 23. OaObOcβaƔbcαВневписанная окружность- это окружность, касающаяся одной стороны
- 24. Скачать презентацию
- 25. Похожие презентации








Слайд 2
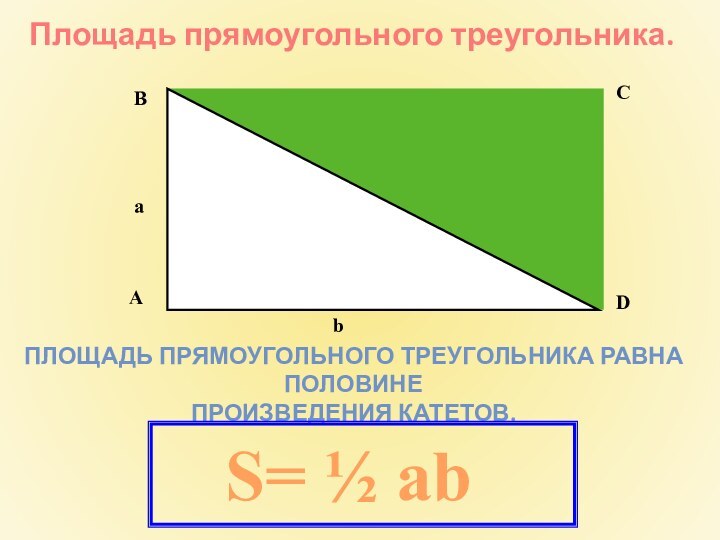
Площадь прямоугольного треугольника.
ПЛОЩАДЬ ПРЯМОУГОЛЬНОГО ТРЕУГОЛЬНИКА РАВНА ПОЛОВИНЕ
ПРОИЗВЕДЕНИЯ КАТЕТОВ.
Слайд 3
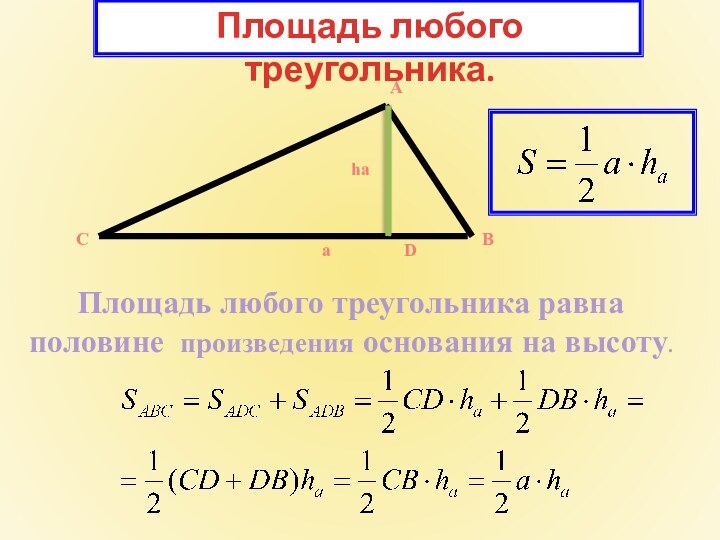
Площадь любого треугольника.
А
a
B
C
D
ha
Площадь любого треугольника равна
половине произведения основания
на высоту.
Слайд 4
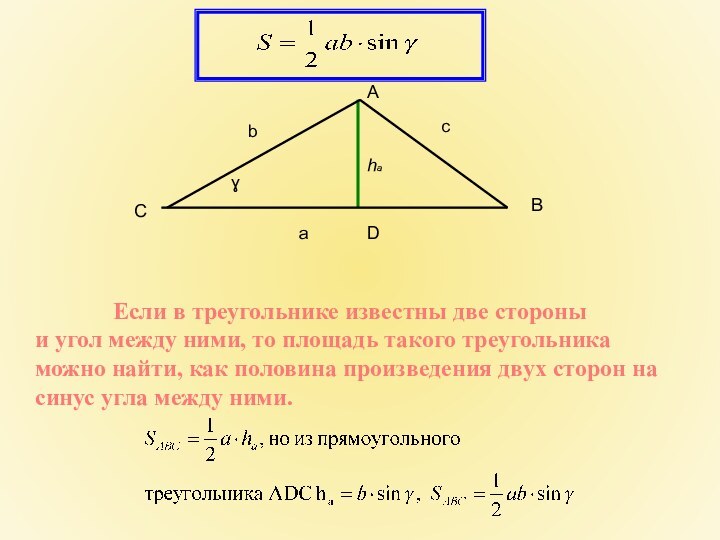
Если в треугольнике известны две стороны
и угол
между ними, то площадь такого треугольника можно найти, как
половина произведения двух сторон на синус угла между ними.С
B
A
ɣ
c
a
D
hа
b
Слайд 5
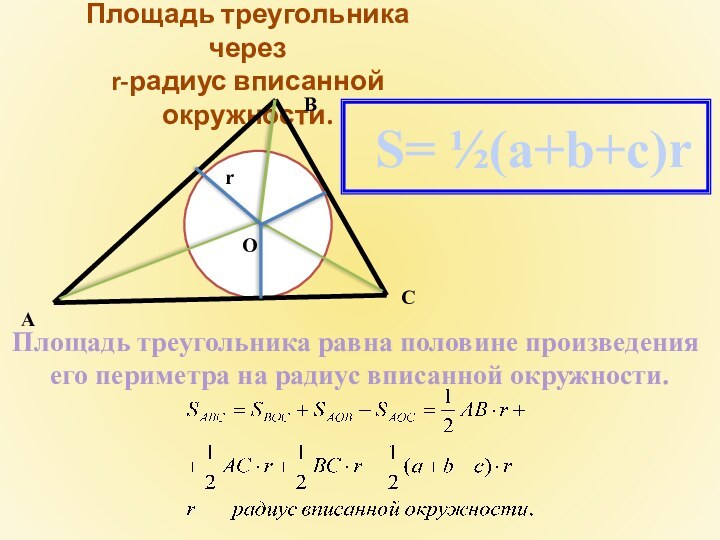
Площадь треугольника через
r-радиус вписанной окружности.
Площадь треугольника равна
половине произведения
его периметра на радиус вписанной окружности.
А
B
C
O
S= ½(a+b+c)r
r
Слайд 6
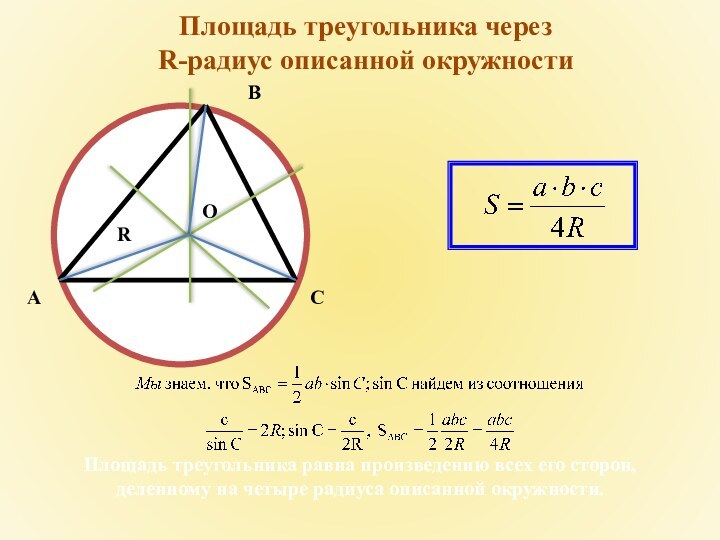
Площадь треугольника через
R-радиус описанной окружности
Площадь треугольника равна
произведению всех его сторон,
деленному на четыре радиуса описанной окружности.
A
B
C
O
R
Слайд 9
ГЕРОН АЛЕКСАНДРИЙСКИЙ (Heronus Alexandrinus)
Герон Александрийский – греческий учёный,
работавший в Александрии,(даты рождения и смерти неизвестны, вероятно, I –
II вв. н. э. ).Математические работы Герона являются энциклопедией античной прикладной математики. В "Метрике" даны правила и формулы для точного и приближённого расчёта различных геометрических фигур, например формула Герона для определения площади треугольника по трём сторонам, правила численного решения квадратных уравнений и приближённого извлечения квадратных и кубических корней. В основном изложение в математических трудах Герона догматично – правила часто не выводятся, а только выясняются на примерах.
Герон занимался геометрией Герон занимался геометрией, механикой Герон занимался геометрией, механикой, гидростатикой Герон занимался геометрией, механикой, гидростатикой, оптикой.
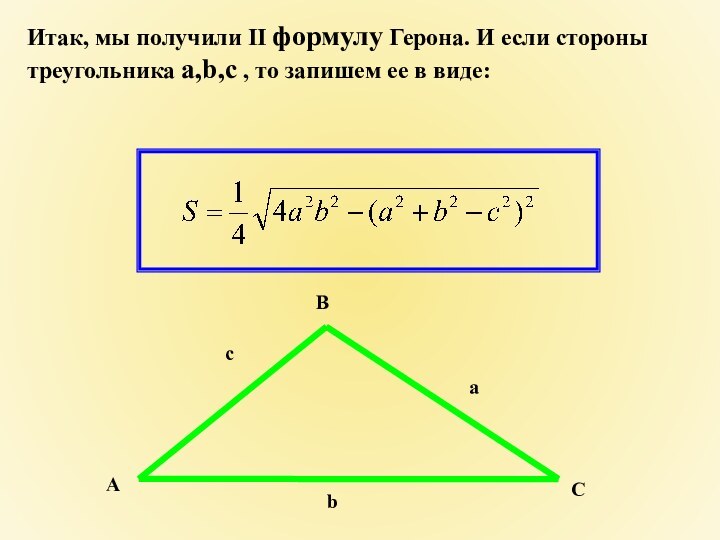
Слайд 11 Итак, мы получили II формулу Герона. И если
стороны треугольника а,b,с , то запишем ее в виде:
C
c
b
B
a
A
Слайд 15
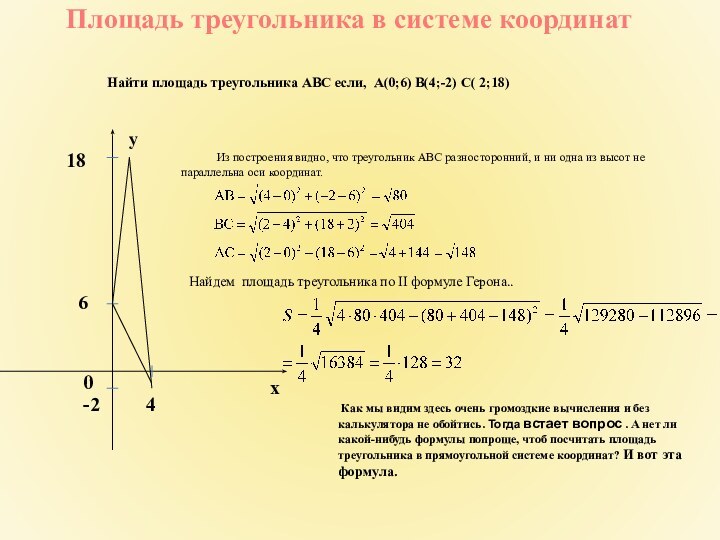
Площадь треугольника в системе координат
Найти площадь треугольника АВС
если, А(0;6) B(4;-2) C( 2;18)
Из построения видно, что
треугольник АВС разносторонний, и ни одна из высот не параллельна оси координат. Найдем площадь треугольника по II формуле Герона..
Как мы видим здесь очень громоздкие вычисления и без калькулятора не обойтись. Тогда встает вопрос . А нет ли какой-нибудь формулы попроще, чтоб посчитать площадь треугольника в прямоугольной системе координат? И вот эта формула.
Слайд 16 Если предположить, что х1=у1=0, то получится еще более
простая формула:
Вывод этой последней формулы приводится ниже .
Пусть вершины треугольника АВС имеют следующие координаты:
А( х1; у1), В (х2; у2), С( х3; у3)
Слайд 17 Пусть требуется найти площадь S треугольника АВС с
вершинами А (х1; у1), В( х2; у2), С( х3;
у3).Пусть АВ= с, АС = b, а углы, образованные этими сторонами осью Ох, соответственно равны α и β
Пусть ф = угол САВ; очевидно
ф = β – α
По известной формуле тригонометрии получаем:
S= ½ bc sin ф = ½ bc sin (β – α) = ½ bc(sin β cos α- cosβ sinα ) = ½(by cx- bx cy) (3)
Отсюда в силу (1) (2) имеем:
S= ½ [(y3-y1) (x2-x1) – (x3-x1) (y2-y1)] (4)
Заметим, что формула (4) при ином расположении вершин может дать площадь треугольника S со знаком минус.
Поэтому формулу для площади треугольника обычно пишут в виде:
S= +/- ½ [(x2-x1) (y3-y1) – (x3-x1) (y2-y1)] (4’)
Где знак выбирается так, чтобы для площади получалось положительное число.
Формулу (4) можно записать в удобном для запоминания форме:





























