Слайд 2
Фракталы: что это?
Фрактал (лат. fractus — дробленый) —
термин, означающий геометрическую фигуру, обладающую свойством самоподобия, то есть
составленную из нескольких частей, каждая из которых подобна всей фигуре целиком.
В более широком смысле под фракталами понимают множества точек в евклидовом пространстве, имеющие дробную метрическую размерность (в смысле Минковского или Хаусдорфа), либо метрическую размерность, строго большую топологической.
Слайд 3
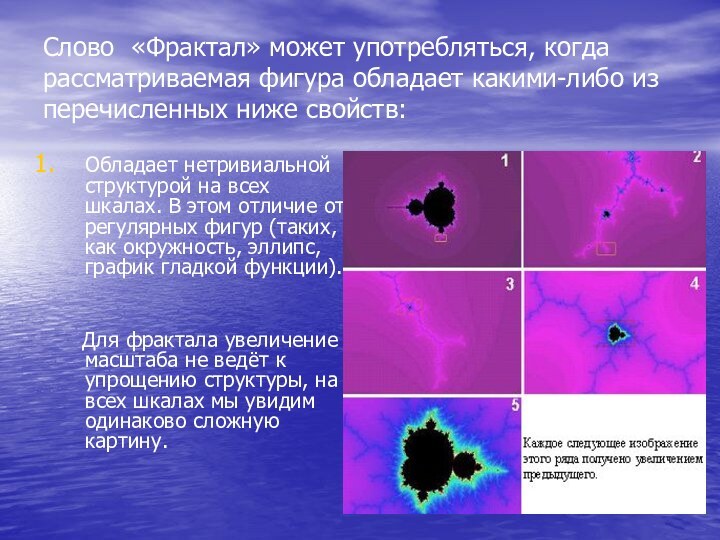
Слово «Фрактал» может употребляться, когда рассматриваемая фигура обладает
какими-либо из перечисленных ниже свойств:
Обладает нетривиальной структурой на всех
шкалах. В этом отличие от регулярных фигур (таких, как окружность, эллипс, график гладкой функции).
Для фрактала увеличение масштаба не ведёт к упрощению структуры, на всех шкалах мы увидим одинаково сложную картину.
Слайд 4
Является самоподобной или приближённо самоподобной.
Слайд 6
Многие объекты в природе обладают фрактальными свойствами, например
побережья, облака, кроны деревьев, кровеносная система и система альвеол
человека или животных.
Слайд 7
И С Т О Р И Я
Первые
примеры самоподобных множеств с необычными свойствами появились в XIX
веке.
Термин «фрактал» был введён Бенуа Мандельбротом в 1975 году и получил широкую популярность с выходом в 1977 году его книги «Фрактальная геометрия природы».
Слайд 8
Примеры:
Самоподобные множества с необычными свойствами в математике
Множество
Кантора (1883) - совершенное множество точек на прямой, не
содержащее ни одного отрезка.
Конструируется следующим образом: на отрезке [0, 1] удаляется интервал (1/3, 2/3), составляющий его среднюю треть; далее из каждого оставшегося отрезка [0, 1/3] и [2/3, 1] также удаляется интервал, составляющий его среднюю треть; этот процесс удаления интервалов продолжается неограниченно; множество точек отрезка [0, 1], оставшееся после удаления всех этих интервалов, и называют канторовым множеством.
Слайд 9
Треугольник Серпинского (1915) — фрактал, один из двумерных
аналогов множества Кантора предложенный польским математиком Серпинским.
Также известен как «решётка» или «салфетка» Серпинского.
Построение. Берётся сплошной равносторонний треугольник, на первом шаге из центра удаляется внутренность срединного треугольника. На втором шаге удаляется три срединных треугольника из трёх оставшихся треугольников и т. д.
Слайд 10
Кривая Коха (1904) -фрактальная кривая описанная шведским математиком
Хельге фон Кохом.
Кривая Коха примечательна тем, что нигде
не имеет касательной, т. е. нигде не дифференцируема, хотя всюду непрерывна.
Построение. Берём единичный отрезок, разделяем на три равные части и заменяем средний интервал равносторонним треугольником без этого сегмента. В результате образуется ломаная, состоящая из четырех звеньев длины 1/3. На следующем шаге повторяем операцию для каждого из четырёх получившихся звеньев и т. д… Предельная кривая и есть кривая Коха.
Слайд 11
Кривая Минковского или колбаса Минковского — классический геометрический
фрактал, предложенный Минковским.
Инициатором является отрезок, а генератором является
ломаная из восьми звеньев (два равных звена продолжают друг друга).
Слайд 12
Применение фракталов
Фракталы широко применяются в компьютерной графике
для построения изображений природных объектов, таких, как деревья, кусты,
горные ландшафты, поверхности морей и т. д.
Слайд 14
В физике фракталы естественным образом возникают при моделировании
нелинейных процессов, таких, как турбулентное течение жидкости, сложные процессы
диффузии-адсорбции, пламя, облака и т. п. Также фракталы используются при моделировании пористых материалов, например, в нефтехимии. В биологии они применяются для моделирования популяций и для описания систем внутренних органов (система кровеносных сосудов).
Слайд 15
В литературе.
Среди литературных произведений находят
такие, которые обладают текстуальной, структурной или семантической фрактальной природой.
В текстуальных фракталах потенциально бесконечно повторяются элементы текста…
Слайд 16
Текстуральные неразветвляющееся, тождественные самим себе с любой итерации.
Например:
«У попа была собака…»
«Притча о философе, которому
снится, что он бабочка, которой снится, что она философ, которому снится…»
«Ложно утверждение, что истинно утверждение, что ложно утверждение…»
Слайд 17
Текстуральные неразветвляющиеся бесконечные тексты с вариациями.
Например:
«У Пегги был весёлый гусь…»
«Дом, который построил
Джек»
Вот дом,
Который построил Джек.
А это пшеница,
Которая в тёмном чулане хранится
В доме,
Который построил Джек.
*****************
Вот два петуха,
Которые будят того пастуха,
Который бранится с коровницей строгою,
Которая доит корову безрогую,
Лягнувшую старого пса без хвоста,
Который за шиворот треплет кота,
Который пугает и ловит синицу,
Которая часто ворует пшеницу,
Которая в темном чулане хранится
В доме, Который построил Джек.
Слайд 18
В структурных фракталах
схема текста потенциально фрактальна
венок сонетов
(15 стихотворений), венок венков сонетов (211 стихотворений), венок сонетов
(2455 стихотворений)
«рассказы в рассказе» («Книга тысячи и одной ночи», Я.Потоцкий «Рукопись, найденная в Сарагоссе»)
предисловия, скрывающие авторство (У.Эко «Имя розы»)
Слайд 19
В децентрализованных сетях Интернет, например Netsukuku .
Система назначения
IP-адресов в сети Netsukuku использует принцип фрактального сжатия информации
для компактного сохранения информации об узлах сети.
Принцип фрактального сжатия информации гарантирует сети децентрализацию, а следовательно, максимально устойчивую работу и возможность быть независимой от контроля государственных и частных структур.