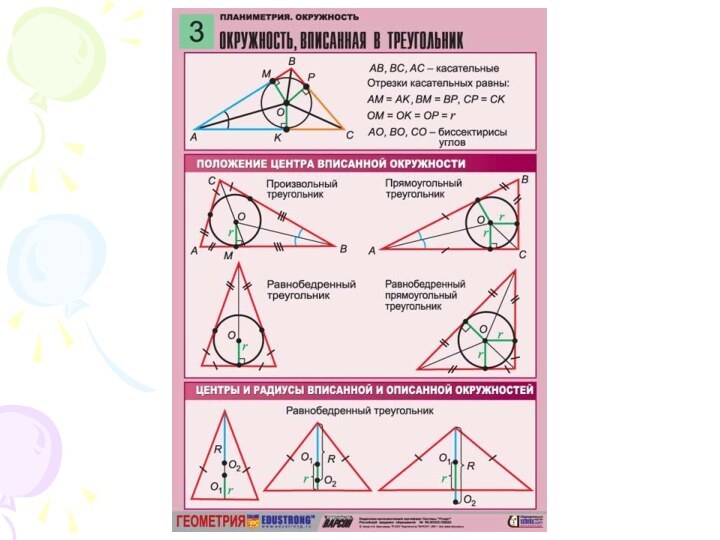
если
все стороны треугольника касаются окружности.Если окружность вписана в треугольник,
то треугольник описан около окружности.
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть











Если окружность вписана в треугольник,
то треугольник описан около окружности.
Доказать: существует Окр.(О;r),
вписанная в треугольник
Доказательство:
Проведём биссектрисы треугольника:АА1, ВВ1, СС1.
По свойству (замечательная точка треугольника)
биссектрисы пересекаются в одной точке – О,
и эта точка равноудалена от всех сторон треугольника, т. е :
SABC = SAOB +SBOC + SAOC = ½ AB · r + ½ BC · r + ½ AC · r =
= ½ (AB + BC + AC) · r = ½ P · r.
P = ½ ·4 · 3 = ½ · 12 = 6(см) - полупериметр
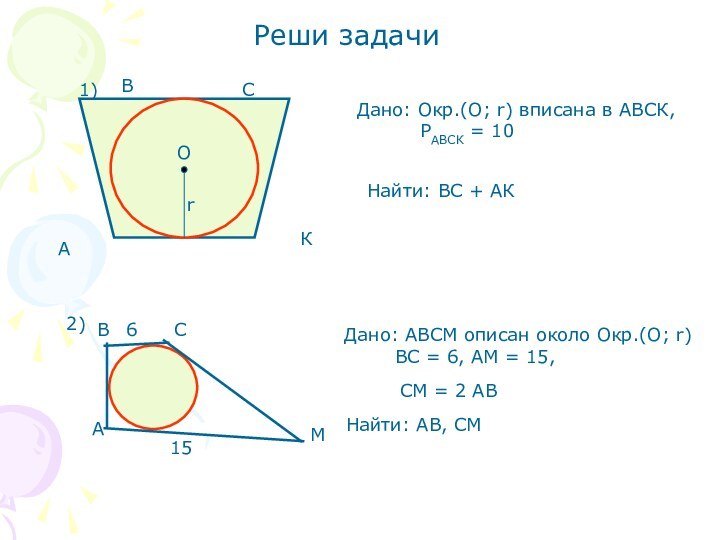
Решение:
2S = (a + b + c) · r
Вывод формулы для радиуса
вписанной в треугольник окружности
Решение:
АВ = АМ + ВМ = 6 + 4 = 10(см)
По теореме Пифагора: АС2 + ВС2 = АВ2
,
АС= 6+ r, ВС = 4 + r
(6 + r)2 + (4 + r)2 = 102
Решив квадратное уравнение, получим r = 2 см
Ответ: 2 см
По свойству касательных: ВЕ = ВМ = а - r
АК = АМ = b - r
AB = AM + BM
c = b – r + a - r
2r = a + b - c
r = ½ (a + b – c)
Т. к. Окр.(О;r) вписана в треугольник АВС,
у которого угол С – прямой, то
АС, ВС, АВ – касательные и
Обратная теорема: если суммы противоположных сторон
выпуклого четырёхугольника равны,
то в него можно вписать окружность.
АВ + СК = ВС + АК.
( доказательство – в учебнике № 724 )
Решение: