переменной х, при которой каждому значению переменной х соответствует
единственное значение переменной у.х – независимая переменная или аргумент
у – зависимая переменная или значение функции
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть






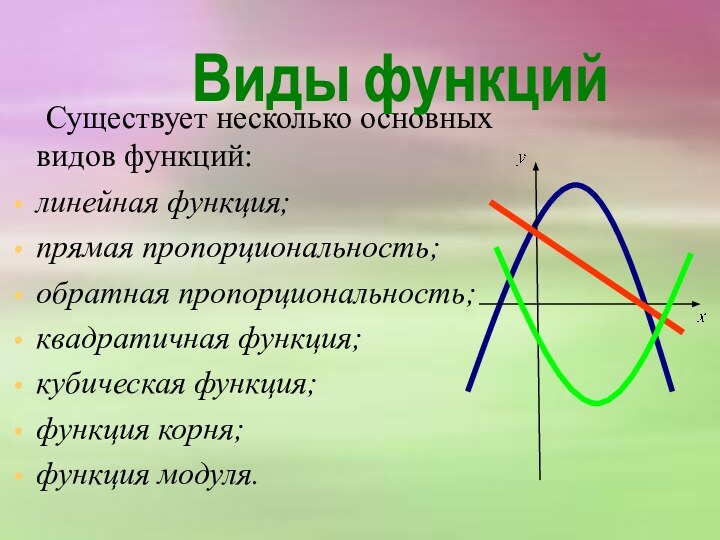





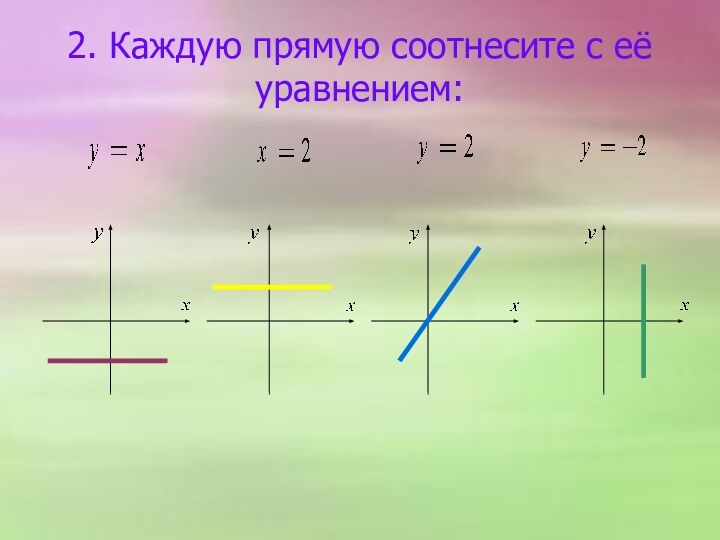
х – независимая переменная или аргумент
у – зависимая переменная или значение функции
Если х = 5, то f(5) = 2 5 + 3=10 + 3 = 13
Если f(х) = 0, то 2х + 3 = 0
2х = -3
х = -1,5
Если функция у = f(х) задана формулой и ее область определения не указана, то считают, что область определения функции состоит из всех значений х, при которых выражение f(х) имеет смысл.
2) f(х) = х +
2
3
x
D(f)=R или D(f) = (- ; + )
3) f(х) =
5x + 2
x - 8
D(f)= (- ; 8) (8; + )
х – 8 0
х 8
8
График функции
X
Y
k>0
k<0
k=0
Прямая пропорциональность
k
x
k>0
k<0
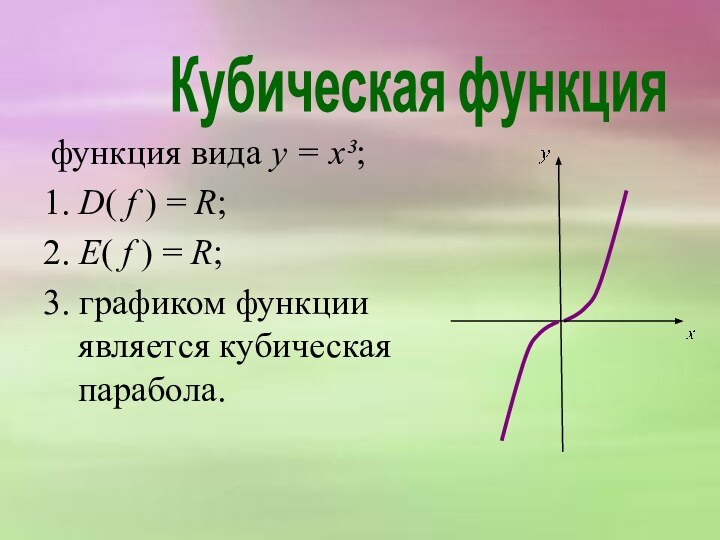
Кубическая функция
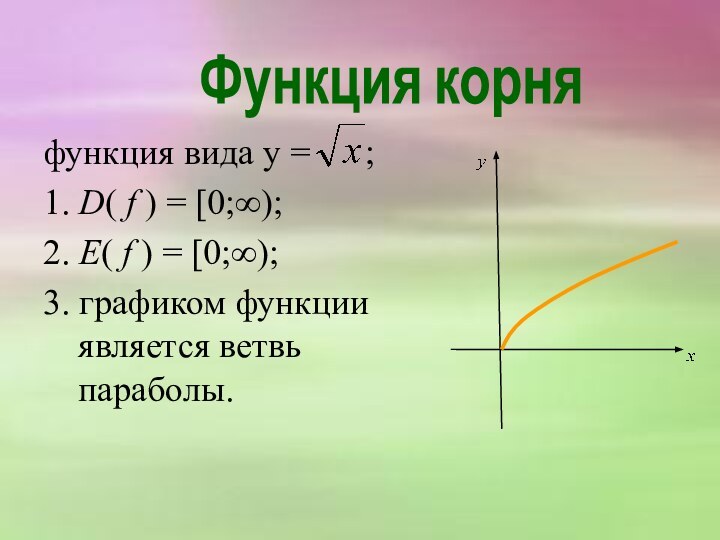
Функция корня
Функция модуля