Презентация на тему Функции тангенса и котангенса

, является нечетной и

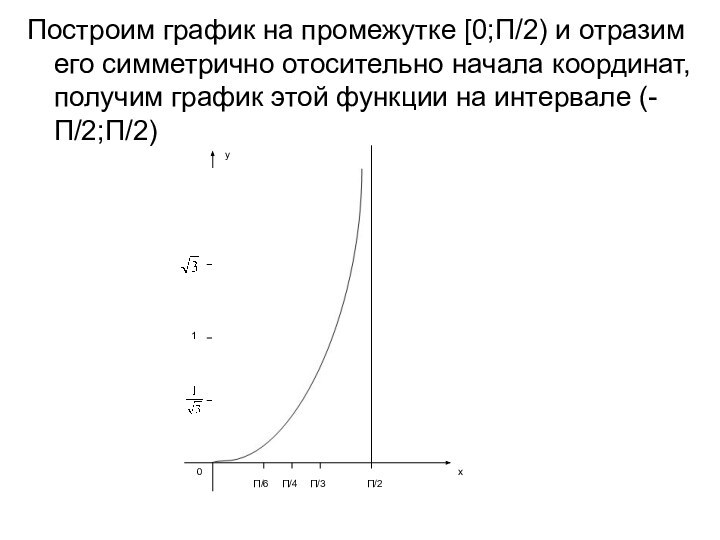
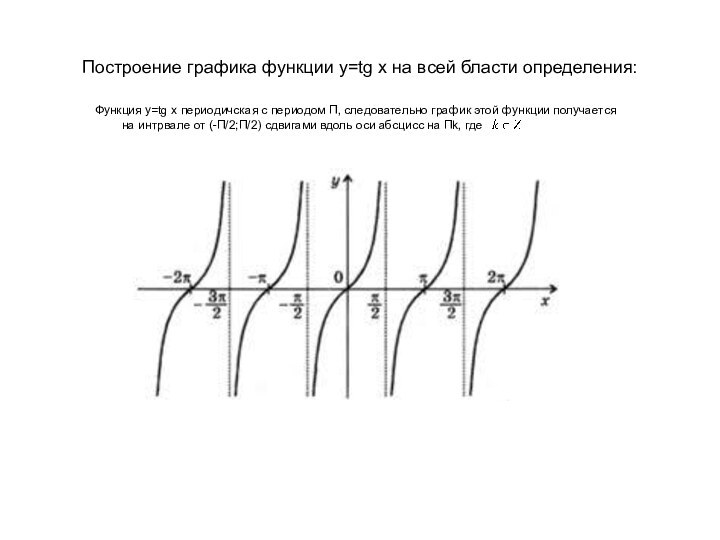
периодической с периодом П.
Покажем, что на промежутке функция y = tgx возратает.
Покажем, что на промежутке функция y = tgx возрастает. Пусть 0≤x1т.е. . По условию 0≤x1свойствам функции у=cos x имеем cos x1> cos x2>0, откуда 0< . Перемножив неравенства sin x1< sin x2
и получим

симметрично отосительно начала координат, получим график этой функции на

интервале (-П/2;П/2)

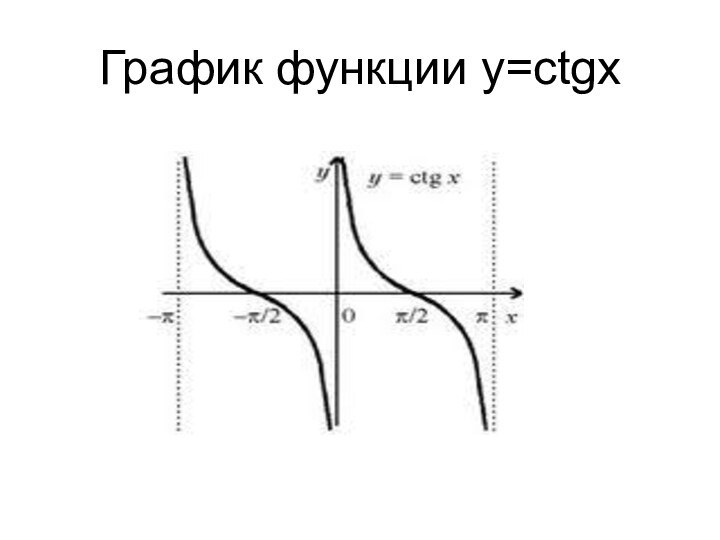
у

х

1

П/6

П/4

П/3

П/2

0

tgx не определена. Если х

П/2, то sin x приближается к 1, а cos, оставаясь положительным, стремится к нулю. При этом дробь возрастает и поэтому график функции y = tgx приближается к вертикальной прямой х=П/2. Аналогично при отрицательных значениях х, больших - П/2 и приближающихся к - П/2 , график функции y = tgx приближается к вертикальной прямой х=-П/2, т.е. прямые х=П/2 и х=-П/2 являются вертикальными асимптотами графика функции.

определения:
Функция у=tg x периодичская с периодом П, следовательно график

этой функции получается на интрвале от (-П/2;П/2) сдвигами вдоль оси абсцисс на Пk, где

определения – множество всех действительных чисел
2)Множество значений R всех действительных чисел.
3)Периодическая с периодам
4)Нечетная.

Положительные значения на интервале

Отрицательные

Возрастающая

принадлежащие отрезку [-П;3П/2]
Построим графики функций у=2 и у= tg

x. Эти графики пересекаются в 3-х точках, абсциссы которых х1, х2, х3 являются корнями уравнения tg x=2. На интервале (-П/2;П/2) уравнение имеет корень х1=arctg2. т.к. функция у=tg х периодическая с периодом П, то х2= arctg2 + П, х3= arctg2 – П.

Ответ: х1=arctg2, х2= arctg2 + П, х3= arctg2 – П.

принадлежащие отрезку [-П;3П/2]
Построим графики функций у=2 и у= tg

x. Из графика видно, что график функции у=tg х лежит не выше прямой у=2 на промежутках [-П;х3], (-П/2;х1] и (П/2;х2].
Ответ: [-П;-П+ arctg2], (-П/2; arctg2], (П/2; П+ arctg2]

> tg П/7
tg 7П/8 и tg 8П/9
tg 7П/8

< tg 8П/9

tg (-7П/8) и tg (-8П/9)
tg (-7П/8) > tg (-8П/9)

tg (-П/5) и tg (-П/7)
tg (-П/5) > tg (-П/7)

tg 2 и tg 3
tg 2 < tg 3

tg 1 и tg 1,5
tg 1 < tg 1,5

этого тождества следует, что для построения графика ctg необходимо

сдвинуть график tg на п/2 влево вдоль оси 0x и отразить полученную кривую относительно оси 0х.Графики tg и ctg состоят из бесконечного множества одинаковых периодически повторяющихся ветвей.

чисел
Множество значений- множество R всех действительных чисел
Функция у=ctgx

периодическая с периодом Т=П
Функция у=ctgx нечетная
Функция у=ctgx принимает значения, равные нулю при
-положительные значения на интервалах
-отрицательные значения на интервалах
Функция у=ctgx является убывающей на каждом интервале