- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему О построении касательной к окружности
Содержание
- 2. Цель работы: рассмотрение способов построения к окружности касательной, проходящей через точку А, не принадлежащую данной окружности.
- 3. 1 способ Традиционное построение касательной циркулем и линейкой
- 4. 2 способ Построим окружность ω1 (А, |АО|) и
- 5. 3 способ Проводим окружность ω1 (А, |АО|) (см.
- 6. 4 способ Чтобы сделать построение, проведем окружность
- 7. 5 способ Строим последовательно окружность ω1 (А, |АО|),
- 8. 6 способПроведем прямую ОА, пересекающую окружность ω
- 9. 6 способ (продолжение)Заметим, что прямая KL перпендикулярна
- 10. Сопоставляя (1) и (2), получаем |PD|:|PA| =
- 11. 7 способСпособ построения касательной только циркулем, т.
- 12. 7 способ (продолжение)Для этого строим окружности ω2
- 13. Если на отрезке AQ как на диаметре
- 14. Так, строим окружность ω (А, |АР|), пересекающую
- 15. Построение касательной можно выполнить просто, если не
- 16. Пусть искомая касательная АВ пересекает касательную l
- 17. Наиболее простое построение точки S такое: откладываем
- 18. Спасибо за внимание!
- 19. Список использованной литературыСкопец З. А. «Геометрические миниатюры»
- 20. Скачать презентацию
- 21. Похожие презентации












Слайд 2 Цель работы: рассмотрение способов построения к окружности касательной,
проходящей через точку А, не принадлежащую данной окружности.
Слайд 3
1 способ
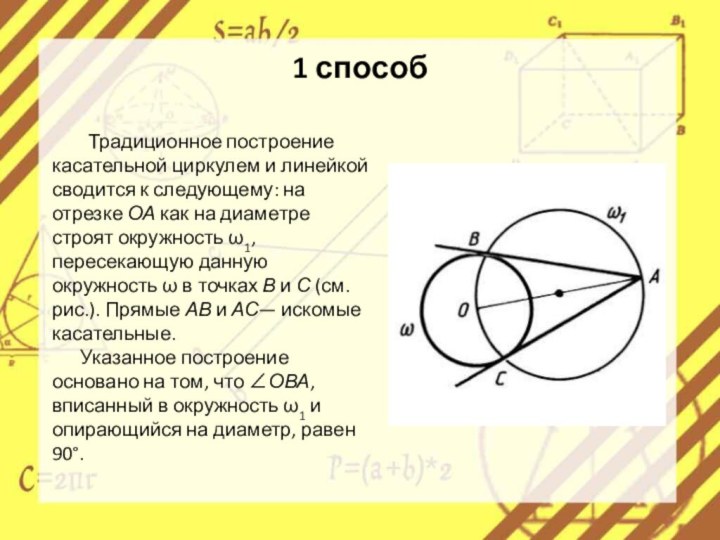
Традиционное построение касательной циркулем и линейкой сводится
к следующему: на отрезке ОА как на диаметре строят
окружность ω1, пересекающую данную окружность ω в точках В и С (см. рис.). Прямые АВ и АС— искомые касательные.Указанное построение основано на том, что ∠ОВА, вписанный в окружность ω1 и опирающийся на диаметр, равен 90°.
Слайд 4
2 способ
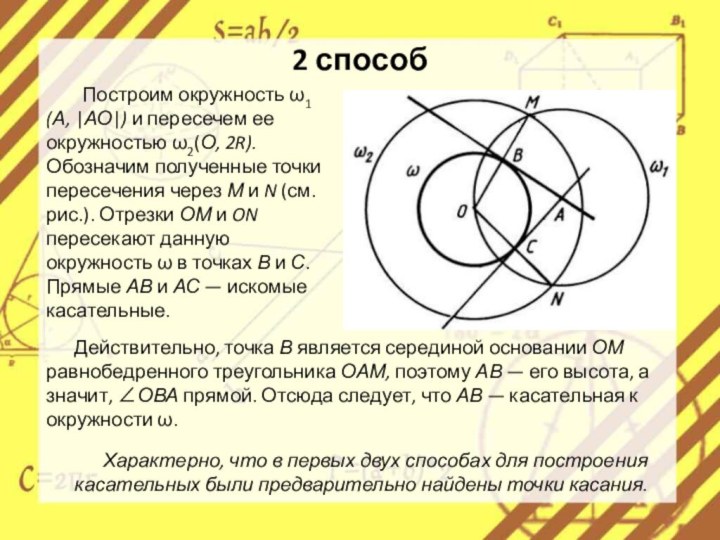
Построим окружность ω1 (А, |АО|) и пересечем
ее окружностью ω2(О, 2R). Обозначим полученные точки пересечения через
М и N (см. рис.). Отрезки ОМ и ON пересекают данную окружность ω в точках В и С. Прямые АВ и АС — искомые касательные.Характерно, что в первых двух способах для построения касательных были предварительно найдены точки касания.
Действительно, точка В является серединой основании ОМ равнобедренного треугольника ОАМ, поэтому АВ — его высота, а значит, ∠ОВА прямой. Отсюда следует, что АВ — касательная к окружности ω.
Слайд 5
3 способ
Проводим окружность ω1 (А, |АО|) (см. рис.).
Строим в точке Р= ω[АО] касательную t к окружности
ω, пересекающую ω1 в точках М и N. Отрезки ОМ и ON пересекают ω в точках В и С; прямые АВ и АС — искомые касательные.Действительно, треугольники РОМ и ВОА конгруэнтны, так как у них общий угол при вершине О, заключенный между соответственно конгруэнтными сторонами (|OР| = |OВ|, |ОМ| = |ОА|). Но треугольник ОРМ прямоугольный, (∠P = 90°). поэтому ∠B = 90°, и, следовательно, прямая АВ — касательная к окружности ω.
Построение касательной к окружности, содержащееся в третьей книге «Начал» Евклида (предложение 17).
Слайд 6
4 способ
Чтобы сделать построение, проведем окружность ω2
(N, |АМ|). Одна из этих двух точек пересечения ω2
и ω1 и есть точка Q, а именно та, для которой направленный угол МОА равен направленному углу NOQ.Построение второй касательной к окружности ω сводится к выполнению поворота , при котором точка N переходит в точку А. В этом случае точка М переходит в точку S и прямая AS — вторая касательная.
Построение касательной к окружности без предварительного построения точек касания.
Проведем окружность ω1 (А, |АО|). Касательная к окружности ω в произвольной точке Р0∈ω пересекает окружность ω1 в точках М и N (см. рис.). Поворот , при котором М → А, отображает точку N на точку Q. Прямая AQ — искомая касательная. Действительно, поворот отображает касательную к ω на касательную к ω ((MN) → (AQ)).
Слайд 7
5 способ
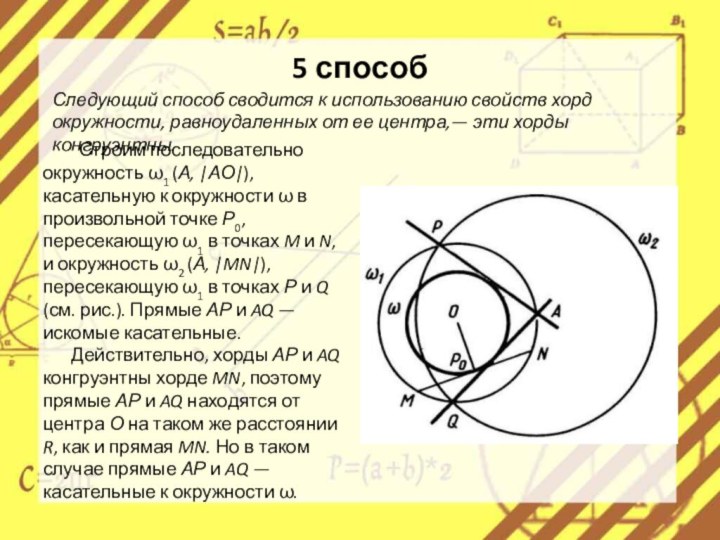
Строим последовательно окружность ω1 (А, |АО|), касательную
к окружности ω в произвольной точке Р0, пересекающую ω1
в точках M и N, и окружность ω2 (А, |MN|), пересекающую ω1 в точках Р и Q (см. рис.). Прямые АР и AQ — искомые касательные.Действительно, хорды АР и AQ конгруэнтны хорде MN, поэтому прямые АР и AQ находятся от центра О на таком же расстоянии R, как и прямая MN. Но в таком случае прямые АР и AQ — касательные к окружности ω.
Следующий способ сводится к использованию свойств хорд окружности, равноудаленных от ее центра,— эти хорды конгруэнтны.
Слайд 8
6 способ
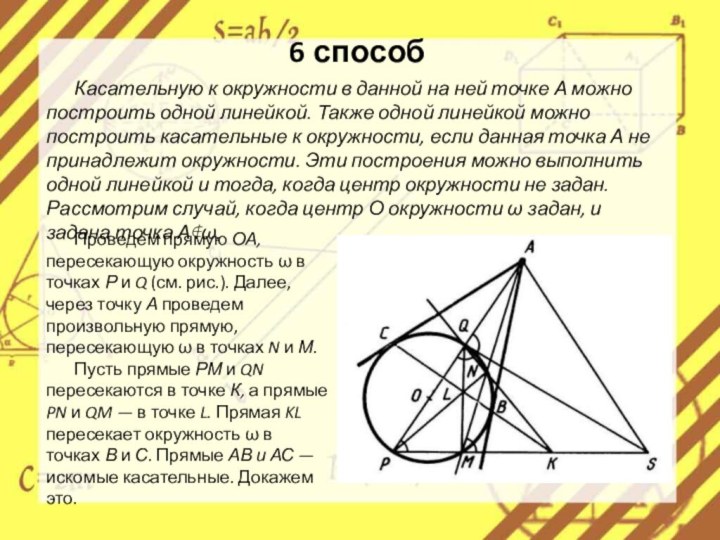
Проведем прямую ОА, пересекающую окружность ω в
точках Р и Q (см. рис.). Далее, через точку
А проведем произвольную прямую, пересекающую ω в точках N и М.Пусть прямые РМ и QN пересекаются в точке К, а прямые PN и QM — в точке L. Прямая KL пересекает окружность ω в точках В и С. Прямые АВ и АС — искомые касательные. Докажем это.
Касательную к окружности в данной на ней точке А можно построить одной линейкой. Также одной линейкой можно построить касательные к окружности, если данная точка А не принадлежит окружности. Эти построения можно выполнить одной линейкой и тогда, когда центр окружности не задан. Рассмотрим случай, когда центр О окружности ω задан, и задана точка А∉ω.
Слайд 9
6 способ (продолжение)
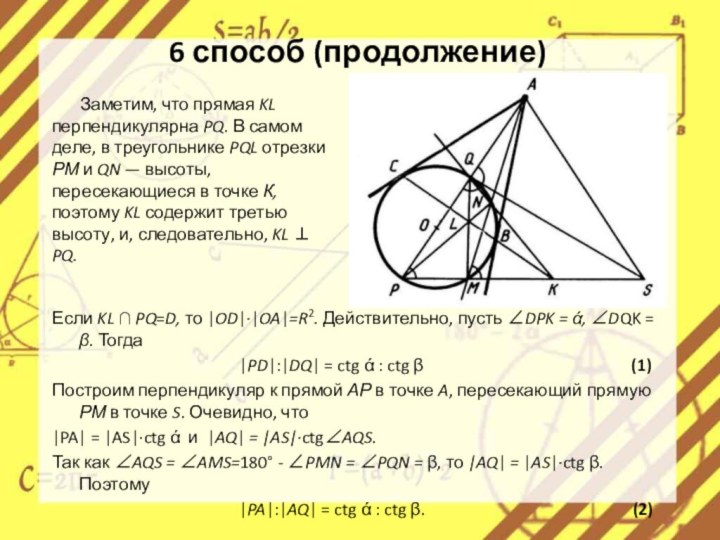
Заметим, что прямая KL перпендикулярна PQ.
В самом деле, в треугольнике PQL отрезки РМ и
QN — высоты, пересекающиеся в точке К, поэтому KL содержит третью высоту, и, следовательно, KL ⊥ PQ.Если KL ∩ PQ=D, то |OD|∙|OA|=R2. Действительно, пусть ∠DPK = ά, ∠DQK = β. Тогда
|PD|:|DQ| = ctg ά : ctg β (1)
Построим перпендикуляр к прямой АР в точке A, пересекающий прямую РМ в точке S. Очевидно, что
|PA| = |AS|∙ctg ά и |AQ| = |AS|∙ctg∠AQS.
Так как ∠AQS = ∠AMS=180° - ∠PMN = ∠PQN = β, то |AQ| = |AS|∙ctg β. Поэтому
|PA|:|AQ| = ctg ά : ctg β. (2)
Слайд 10 Сопоставляя (1) и (2), получаем |PD|:|PA| = |DQ|:
|AQ|, или
(|OD| + R)∙(|OA| - R) = (R -
|OD|)∙(|OA|+R). После раскрытия скобок и упрощений находим, что
|OD|∙|OA|=R2. (3)
Из соотношения (3) следует, что |OD|:R = R:|OA|, т. е. треугольники ODB и ОВА подобны. Поскольку ∠ODB = 90°, то ∠OBA = 90°. Следовательно, прямая АВ - искомая касательная.
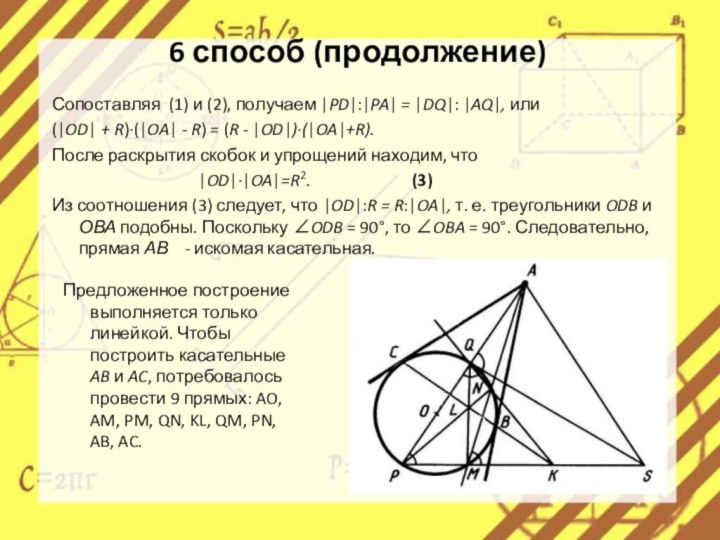
6 способ (продолжение)
Предложенное построение выполняется только линейкой. Чтобы построить касательные AB и AC, потребовалось провести 9 прямых: AO, AM, PM, QN, KL, QM, PN, AB, AC.
Слайд 11
7 способ
Способ построения касательной только циркулем, т. е.
без привлечения линейки построим точки касания В и С
по заданным окружности ω (О, R) и точке А∉ω.Проведем окружность ω1 (А, |ОА|) см. (рис.). Далее найдем раствор циркуля, равный 2R, для чего выберем на окружности ω точку S и отложим три дуги, содержащие по 60 дуговых градусов: ∪SP = ∪PQ = ∪QT = 60°. Точки S и Т диаметрально противоположны. Строим окружность (О, |ST|), пересекающую ω1 в точках М и N. Теперь остается одним циркулем построить середину отрезка МО.
Слайд 12
7 способ (продолжение)
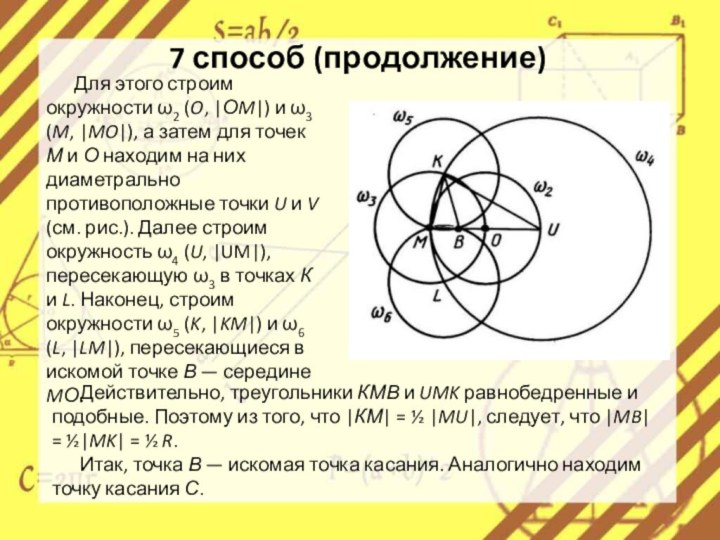
Для этого строим окружности ω2 (O,
|ОM|) и ω3 (M, |MO|), а затем для точек
М и О находим на них диаметрально противоположные точки U и V (см. рис.). Далее строим окружность ω4 (U, |UM|), пересекающую ω3 в точках К и L. Наконец, строим окружности ω5 (K, |KM|) и ω6 (L, |LM|), пересекающиеся в искомой точке В — середине MО.Действительно, треугольники КМВ и UMK равнобедренные и подобные. Поэтому из того, что |КМ| = ½ |MU|, следует, что |MB| = ½|MK| = ½ R.
Итак, точка В — искомая точка касания. Аналогично находим точку касания С.
Слайд 13 Если на отрезке AQ как на диаметре построить
окружность ω1 и пересечь ее касательной l, проведенной в
точке Р к ω, то получим точки М и N.Очевидно, |АМ|2=|АР|∙|AQ|. Поэтому окружность ω2 (А, |АМ|) пересечет ω в точках В и С касания искомых касательных АВ и АС.
8 способ
Еще одно построение касательной к окружности основано на следующем свойстве отрезков секущей, проведенной к окружности( см. рис.):
|AB|2=|AP|∙|AQ|
Слайд 14 Так, строим окружность ω (А, |АР|), пересекающую (АР)
в точке D, затем строим окружность ω2 на диаметре
QD и пересекаем ее перпендикуляром к прямой АР в точке А. Для полученных точек М и N имеем:|AM|2=|AN|2=|AD|∙|AQ| = |AP|∙|AQ|,
поэтому окружность ω3 (А, |AМ|) пересекает ω в искомых точках касания В и С.
8 способ (продолжение)
Другой вариант построения касательной в данном случае основан на ином способе построения отрезка АВ по отрезкам АР и AQ (см. рис.).
Слайд 15 Построение касательной можно выполнить просто, если не связывать
его непосредственно с данной окружностью ω(О, R) и данной
точкой А. Если В есть точка касания, то треугольник ОАВ прямоугольный, причем известно, что |ОВ|=R, |OA|=d, ∠В=90°. Следовательно, задача сводится к построению прямоугольного треугольника по катету и гипотенузе. Катет АВ построенного треугольника позволяет строить окружность ω1 (А, |АВ|), пересекающую ω в искомых точках В и С.9 способ
Слайд 16 Пусть искомая касательная АВ пересекает касательную l к
ω(О, R) в ее точке Q в некоторой точке
М (см.рис.). Очевидно, [МО) — биссектриса угла ∠QMA. Биссектриса угла, смежного с ∠QMA, пересекает прямую АР в точке S, для которой|QS| : |SA| = |QO|:|OA|.
Построив точку S, можно построить окружность ω1 на диаметре OS. Поскольку ∠SMO прямой, то ω1 пересечет l в точках М и N, таких, что (AM) и (AN) — искомые касательные.
10 способ
Приведем еще одно построение, основанное на свойствах биссектрис
треугольника.
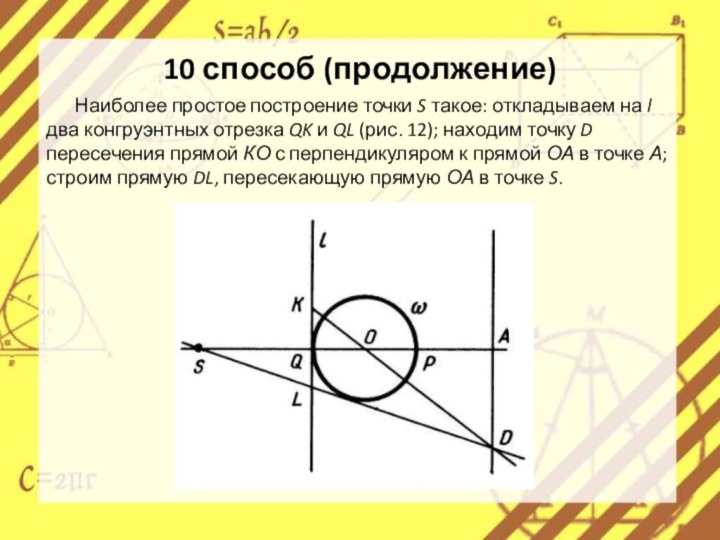
Слайд 17 Наиболее простое построение точки S такое: откладываем на
l два конгруэнтных отрезка QK и QL (рис. 12);
находим точку D пересечения прямой КО с перпендикуляром к прямой ОА в точке А; строим прямую DL, пересекающую прямую ОА в точке S.10 способ (продолжение)